简介:PID控制器是自动化控制领域中用于优化系统性能的算法。z-nPID整定方法和差分进化算法(DE)是提高PID控制器性能的两种关键技术。本压缩包内含相关源码,通过这些代码,开发者可以学习如何实施z-nPID整定,以及如何利用差分进化算法进行PID参数的自动优化。理解这些策略对于提升系统控制的稳定性和响应速度至关重要。 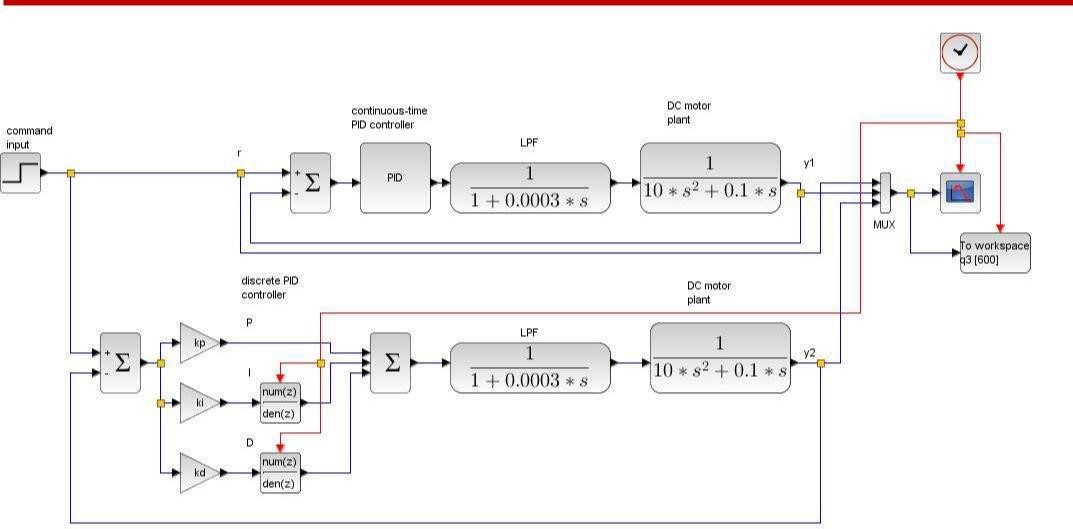
1. PID控制器概述
1.1 PID控制器的发展历史
1.1.1 PID控制器的起源
PID控制器的历史可以追溯到20世纪初,它的雏形是工业工程师们为了解决过程控制中的非线性、时变和滞后性问题而创造的一种简单而有效的控制技术。最初,工程师们通过模拟电路来实现比例(Proportional)、积分(Integral)和微分(Derivative)的控制算法,这些电路能够根据系统的实际输出与期望输出之间的差异(误差)来调整控制量,以达到对温度、压力、流量等工业过程变量的精确控制。
1.1.2 PID技术的演进
随着时间的推移,PID控制器从最初的模拟设备发展到数字控制器,其算法也从纯手工调整演变为各种智能化的参数整定方法。现在,PID控制器已经被集成到各种先进的控制系统中,不仅在工业生产中发挥作用,也被应用于家用电器、汽车、航空航天等众多领域。
1.2 PID控制器的工作原理
1.2.1 PID控制器的组成结构
PID控制器主要由三个基本控制环节组成:比例(P)、积分(I)和微分(D),这三个环节通过线性组合形成一个反馈回路。比例环节提供即时的误差响应,积分环节消除稳态误差,而微分环节预测未来的误差变化趋势,对控制动作进行微调。控制器的输出通过放大器放大后作用于被控对象,从而实现对系统的精确控制。
1.2.2 PID算法的工作流程
在工作流程中,PID算法首先需要确定三个参数:比例系数(Kp)、积分时间常数(Ki)和微分时间常数(Kd)。控制器根据设定的目标值(Setpoint)和实际检测到的过程变量(Process Variable)计算误差(Error),然后将误差分别通过P、I、D三个环节处理后相加,生成最终的控制输出。整个过程是一个闭环反馈控制系统,能够根据控制对象的动态响应不断调整控制量,实现稳定控制。
1.3 PID控制器的应用领域
1.3.1 工业控制中的PID应用
在工业控制中,PID控制器因其结构简单、易于理解且鲁棒性强等优点,被广泛应用于温度控制、压力控制、流量控制和液位控制等过程。工程师可以根据不同的控制对象和环境特点调整PID参数,以适应各种复杂的工况。
1.3.2 PID在现代技术中的创新应用
现代技术中,PID控制已经不再局限于传统的模拟硬件实现。随着计算机技术的发展,数字PID控制器越来越多地取代了传统的模拟控制器,并在人工智能、机器学习等前沿技术的辅助下,实现了更高级的自适应和预测控制策略。PID控制器的智能化调优,使得其在精确度和效率方面达到了新的高度,展现了广阔的应用前景。
2. 比例-积分-微分(P-I-D)控制器的三个组成部分
2.1 比例(Proportional)控制的作用与调整
比例控制是PID控制器中最直观的部分,它根据当前的误差值来调整控制输出。在物理系统中,控制输出与误差值成比例关系,因此,比例控制器的输出是误差信号的直接函数。
2.1.1 比例控制原理
比例控制的核心在于误差的大小决定了控制力度的强弱。当误差较大时,控制器会产生较大的控制作用;反之,误差较小时,则减小控制作用。这样的设计可以使得系统更快地响应误差,减少误差累积。
2.1.2 比例增益的确定与调整
比例增益(Kp)是比例控制器中一个关键的调节参数,它决定了输出与误差信号之间比例关系的强度。在实际应用中,Kp的调整通常会经历一个反复尝试的过程,需要兼顾系统的快速响应和稳定性。增益太大可能会导致系统振荡,而增益太小则可能使系统响应过慢。
# 示例代码:比例控制器的增益调整
def proportional_control(error, Kp):
"""
实现比例控制的函数。
:param error: 当前误差
:param Kp: 比例增益
:return: 控制器输出
"""
output = Kp * error
return output
# 参数说明和逻辑分析:
# Kp为比例增益参数,其值决定了误差对输出的影响程度。
# error是当前系统的误差信号,它可以是期望值与实际输出值之间的差值。
# 输出output是经过比例控制器调整后的控制信号,它将被用来调节系统以减小误差。
2.2 积分(Integral)控制的作用与调整
积分控制的主要目的是消除稳态误差,即长期累积的误差。积分控制器通过累积误差的总和来增加控制作用,直到误差趋于零。
2.2.1 积分控制原理
积分控制动作的大小取决于误差信号的持续时间和幅度。误差持续存在越久,积分控制的作用就越强。积分控制常用于处理那些静态误差不能被比例控制消除的情况。
2.2.2 积分时间常数的设定与优化
积分时间常数(Ti)是积分控制器中的关键参数,它决定了积分作用的速率。Ti较大时,积分作用较为缓慢;Ti较小,则积分作用迅速。Ti的选择需要在消除稳态误差和避免系统振荡之间取得平衡。
graph LR
A[开始积分作用] --> B{误差是否存在}
B -- 是 --> C[累积误差值]
B -- 否 --> D[重置积分项]
C --> E[根据Ti调整积分输出]
D --> A
E --> F[系统输出调整]
2.3 微分(Derivative)控制的作用与调整
微分控制基于误差变化的趋势来调整控制动作,它对快速变化的误差尤为敏感。在误差变化较大时,微分控制器会产生较大的控制作用,有助于快速抑制系统的振荡。
2.3.1 微分控制原理
微分控制试图预测误差的变化趋势,并基于这一预测进行干预。它通过计算误差的变化率来评估误差未来的发展趋势,并据此进行干预。
2.3.2 微分时间常数的选择与调试
微分时间常数(Td)是微分控制中的重要参数。Td过大可能会导致控制作用对噪声过于敏感,而Td过小则可能无法充分抑制振荡。正确设置Td需要细致的调试和评估。
# 示例代码:微分控制器的实现
def derivative_control(error, Td, prev_error):
"""
实现微分控制的函数。
:param error: 当前误差
:param Td: 微分时间常数
:param prev_error: 上一次的误差值
:return: 控制器输出
"""
derivative = (error - prev_error) / Td
return derivative
# 参数说明和逻辑分析:
# Td是微分时间常数,它决定了微分控制响应误差变化的速率。
# error是当前误差值,prev_error是上一次的误差值。
# derivative是误差变化率的估计,控制器输出将根据此估计进行调整。
通过调整比例、积分和微分三个组成部分的参数,我们可以实现对PID控制器的精细调节,以达到最佳的控制性能。这在实际中往往需要反复的实验和调整,特别是在遇到复杂或非线性系统时。下一章我们将深入探讨PID参数整定的方法和对系统瞬态响应的改善。
3. z-nPID整定方法及其对系统瞬态响应的改善
3.1 z-nPID整定方法的理论基础
3.1.1 z-N法的基本思想
z-N法,即Ziegler-Nichols方法,是一种经典的PID控制器参数整定方法。它通过对控制系统的开环响应进行分析,进而确定PID参数。z-N法的核心思想是:通过实验观测系统对阶跃输入的响应来估算系统的动态特性,然后根据这些特性选择合适的比例、积分、微分增益。
在实际应用中,z-N法首先要求操作者手动控制系统,记录下系统对阶跃输入的响应曲线。通过分析响应曲线,可以得到临界比例带宽(Ku)和临界振荡周期(Tu),这两个参数是z-N法进行参数整定的基础。z-N法提供了一套经验公式,根据临界参数计算出PID控制器的P、I、D三个参数。
3.1.2 n参数的作用与选择
在z-N法中,n参数是决定PID控制器响应速度和稳定性的关键变量。该参数定义了控制器输出变化的程度,其值的选择对于确保系统稳定性和快速响应至关重要。通常,n的值越大,控制器的反应越温和;n的值越小,控制器响应越快,但过小的n值可能导致系统变得不稳定。
在实践中,选择合适的n值需要在系统快速响应和稳定性之间进行权衡。z-N法提供了两套参数设定规则:一种是针对比例控制器(P)的参数整定,另一种是针对比例-积分(PI)和比例-微分(PD)控制器的参数整定。对于PID控制器的整定,则需要根据实际系统的响应特性,合理选择n参数,并结合经验公式进行调整。
3.2 z-nPID整定对系统瞬态响应的影响
3.2.1 系统瞬态响应的评价指标
系统瞬态响应通常是指系统受到外加输入信号后的暂时性动态响应,包括上升时间、超调量、调整时间等关键指标。其中,上升时间衡量的是系统响应从稳态值的10%上升到90%所需的时间;超调量是指系统输出首次超过最终稳态值的最大幅度;调整时间是指系统响应从第一次达到并保持在最终稳态值的±5%范围内的整个时间区间。
对于控制系统而言,良好的瞬态响应意味着系统能够快速且准确地达到稳态,同时尽量减少超调和振荡。理想的瞬态响应曲线应当是快速上升且平滑过渡到稳态,不应有大的振荡或过冲。
3.2.2 z-nPID整定在提升瞬态响应中的优势
z-nPID整定方法的显著优势在于其简便性和实用性,通过经验公式直接给出一组可用的PID参数。尽管它并不保证得到最优参数,但通常可以在第一轮测试中就得到一个性能良好的系统。在瞬态响应方面,z-nPID整定法能够快速调整参数,从而使得系统具有较短的上升时间和调整时间,同时控制超调量在一个可接受的范围内。
采用z-nPID整定后的系统,往往能够更快地达到稳态,而且系统的超调幅度会减小,这使得系统更加稳定且对瞬态变化的适应性更强。对于那些对瞬态响应要求较高的应用,如快速位置控制、温度控制等,z-nPID整定能够显著提升系统性能。
3.3 z-nPID整定的实践操作步骤
3.3.1 参数设定与初始化
在进行z-nPID整定时,首先要对系统进行设定,设置初始参数。这包括控制器的初始比例增益(P)、积分时间(Ti)、微分时间(Td),以及初始的系统运行条件。在操作前,要确保系统处于静态状态,没有外加的干扰和扰动。
接下来,操作人员需要逐步增加比例增益,直到系统输出开始出现持续的振荡,此时的增益称为临界比例增益(Ku),临界振荡周期为(Tu)。然后,根据z-N法提供的公式,根据Ku和Tu计算出PI和PD控制器参数。
3.3.2 整定过程的调整策略
在得到一组初步的参数后,需要对系统进行实际的闭环测试。测试过程中需要观察系统响应,如果响应不满意,比如响应过慢或有较大的超调,那么就需要对参数进行微调。调整策略可能包括增减比例增益、调整积分时间或微分时间等。参数调整过程中需要反复测试,记录数据,直到系统响应达到设计的要求。
值得注意的是,z-nPID整定方法虽然有其局限性,但在多数情况下,它的实用性很强,能够快速得到一个稳定且满意的控制效果。对于复杂系统,可能需要结合其他高级控制理论和工具来进一步优化PID参数。在实践中,z-nPID整定是控制工程师们进行PID控制器参数设定的常用手段,尤其是在系统设计的初期阶段,快速获得一个性能合理的控制策略。
4. 差分进化算法在PID参数自动整定中的应用
4.1 差分进化算法简介
4.1.1 差分进化算法的概念
差分进化(Differential Evolution, DE)是一种简单而强大的全局优化算法,它属于进化算法(Evolutionary Algorithms, EAs)的一种。差分进化算法通过模拟自然界中的进化过程,在给定的目标函数上进行迭代搜索,寻找最优解。与遗传算法类似,差分进化同样包括选择、交叉(混合)和变异这三个基本操作,但其核心思想是基于种群中的个体差分向量的利用。
4.1.2 算法的工作原理与特点
差分进化算法的工作原理是初始化一个种群,这个种群由一定数量的个体组成,每个个体代表了问题的一个潜在解。在迭代过程中,算法通过差分向量来引导搜索过程,逐步优化个体,直至找到满足停止条件的最优解。具体来说,差分进化算法的特点包括:
- 简单:算法结构简单,容易实现。
- 鲁棒:对于不同类型的优化问题均展现出良好的全局搜索能力。
- 强调种群多样性:差分进化维持种群多样性,减少早熟收敛的可能性。
4.2 差分进化算法在PID整定中的作用
4.2.1 利用差分进化优化PID参数
在PID控制器的参数整定中,差分进化算法能够通过其强大的全局搜索能力,在多维参数空间中寻找到使得性能指标最优(例如最小化超调量、调整时间和稳态误差等)的PID参数组合。这一过程涉及到以下步骤:
- 编码 :将PID参数(P,I,D)编码为差分进化算法中的个体。
- 初始化 :生成初始种群。
- 评估 :对种群中的每个个体(即一组PID参数)进行性能评估。
- 选择与变异 :根据评估结果,通过选择和变异操作生成新的种群。
- 交叉 :生成的种群进行交叉操作,以增加种群的多样性。
- 更新 :使用新种群替换旧种群,并重复上述评估、选择、变异、交叉和更新的过程,直至满足终止条件。
4.2.2 算法性能评估与比较
在完成差分进化算法在PID整定中的应用之后,需要对算法的性能进行评估。这通常包括以下几个方面:
- 收敛速度 :算法在达到全局最优解前的迭代次数。
- 求解精度 :算法找到的最优解与理论最优解的接近程度。
- 鲁棒性 :算法在不同初始条件和不同问题上的一致性能。
通过与传统的PID整定方法如Ziegler-Nichols(Z-N)方法比较,可以展示差分进化算法在复杂或非线性系统中优势。另外,与其他进化算法,如遗传算法、粒子群优化等的比较,可以进一步验证差分进化算法在PID参数优化中的应用价值。
4.3 差分进化算法在PID整定中的实践案例
4.3.1 案例分析:控制系统参数优化
以一个具体实例来说明差分进化算法在PID整定中的应用。假设我们有一个简单的温度控制系统,目标是通过PID控制器稳定系统的温度输出。以下是整个优化过程的描述:
- 问题定义 :定义系统的性能指标,例如最小化温度偏差、快速响应等。
- 参数编码 :选择合适的编码方式,将PID参数编码为个体。
- 初始化种群 :随机生成一组初始解。
- 性能评估 :根据系统性能指标,对每个个体进行评估。
- 进化操作 :基于差分进化算法的三个基本操作(选择、变异、交叉)进行迭代。
- 终止条件 :当达到设定的迭代次数或解的质量满足要求时停止迭代。
4.3.2 案例总结:差分进化算法的优势展现
通过上述案例,我们可以总结出差分进化算法在PID整定中的优势,主要体现在:
- 全局搜索能力 :能够有效避免陷入局部最优,找到全局最优解。
- 适应性强 :适用于不同类型的系统模型和复杂性不同的问题。
- 自适应性 :能根据系统的动态调整参数,具有较好的自适应控制性能。
通过使用差分进化算法进行PID参数的优化,控制系统能够实现更稳定、更快的响应,并降低超调量,从而提高整体控制性能。该方法不仅适用于简单的系统,还可以扩展到更复杂、更高维度的控制系统中,成为现代工业自动化领域中不可或缺的工具之一。
5. 源码包含的关键模块:控制器参数初始化、更新规则、误差计算、反馈机制
5.1 控制器参数初始化模块分析
5.1.1 参数初始化的重要性
在实现PID控制器的过程中,参数初始化是一个关键步骤,它为控制器的正常工作奠定了基础。参数初始化不当可能会导致控制过程的不稳定,甚至造成系统的损坏。例如,过大的比例增益可能引起系统振荡,而过小的增益又可能无法有效消除误差。因此,合理地设定PID参数的初始值对于后续的系统调试和优化至关重要。
5.1.2 参数初始化的实现方法
参数初始化的过程通常包括设置初始的P、I、D值。在实践中,这些值往往根据系统的理论知识或者经验进行设定。一种常见的初始化方法是,将P、I、D参数分别初始化为零,然后通过测试和调整来确定最佳值。此外,也可以使用一些预设的规则或者专家系统来自动初始化这些值,例如Ziegler-Nichols方法。
# Python代码示例:PID参数初始化
class PIDController:
def __init__(self, kp, ki, kd):
self.kp = kp # 比例增益
self.ki = ki # 积分增益
self.kd = kd # 微分增益
self.previous_error = 0
self.integral = 0
def update(self, setpoint, measured_value):
error = setpoint - measured_value
self.integral += error
derivative = error - self.previous_error
output = (self.kp * error) + (self.ki * self.integral) + (self.kd * derivative)
self.previous_error = error
return output
在这个代码块中, PIDController 类的初始化方法接受三个参数:比例增益 kp 、积分增益 ki 和微分增益 kd 。这为控制器的进一步操作提供了必要的初始设置。
5.2 PID更新规则的设计与实现
5.2.1 更新规则的设计原则
PID控制器的核心功能是根据设定点和当前测量值的差异,计算出控制系统的输出。更新规则的设计必须遵循几个基本原则:首先,它应该能够快速响应设定值的变化;其次,它需要有良好的稳定性,避免产生过多的超调和振荡;最后,更新规则应保证系统的长期稳定性。
5.2.2 更新规则的代码实现细节
在代码层面,更新规则通过一段算法来实现,该算法根据比例、积分、微分三个部分的贡献,计算出控制器的输出值。
# Python代码示例:PID控制器更新规则的实现
def update_pid_controller(controller, setpoint, measured_value):
error = setpoint - measured_value
controller.integral += error
derivative = error - controller.previous_error
output = (controller.kp * error) + (controller.ki * controller.integral) + (controller.kd * derivative)
controller.previous_error = error
return output
上述代码片段中, update_pid_controller 函数实现了PID控制器的更新规则。它接收控制器对象、设定点和测量值作为输入,并根据计算出的误差、积分和微分来更新控制器的输出。
5.3 误差计算方法及其在PID中的应用
5.3.1 误差的来源与计算方法
误差是PID控制器核心概念之一,它代表了设定点(期望输出)与实际测量值之间的差异。计算误差通常是一个简单的减法操作:误差 = 设定点 - 测量值。这个值对于整个PID控制回路来说至关重要,因为它直接决定了控制器的调整方向和大小。
5.3.2 误差计算在PID性能优化中的作用
通过对误差的连续监控和分析,可以评估PID控制器的表现,并据此调整P、I、D参数以优化系统性能。例如,如果误差的曲线显示系统有较大的振荡,可能需要减少微分作用或增加积分作用来抑制振荡。误差的持续计算和分析是确保系统长期稳定运行的关键。
5.4 反馈机制的设计与作用
5.4.1 反馈机制的理论基础
反馈机制是指控制器接收来自系统的反馈信号,该信号反映了控制器输出对系统的实际影响。在PID控制系统中,反馈机制是实时调整控制参数的依据。没有有效的反馈机制,控制器将无法知晓其输出是否有效地引导了系统的动态行为。
5.4.2 实际系统中反馈机制的实现与调整
在实际的控制系统中,反馈机制通常是通过传感器来实现的。传感器测量系统的相关参数,然后将这些信息传回控制器,控制器根据这些信息来计算和调整其输出。控制器软件中的反馈机制应包括对数据的校验、滤波和异常处理等步骤,以确保反馈数据的准确性和可靠性。
在设计反馈机制时,需要考虑的因素包括但不限于信号的采样率、数据类型和精度、传输延迟、以及可能的噪声干扰。合理的反馈机制设计对于提升PID控制系统的响应速度和控制精度至关重要。
6. PID整定技术的未来发展趋势与挑战
6.1 人工智能技术在PID整定中的应用前景
人工智能(AI)的快速发展为许多领域带来了革命性的变化,PID整定技术也不例外。AI的子领域,如机器学习和深度学习,正被探索和应用于PID控制的各个方面,以期提升其性能和适应性。
6.1.1 机器学习与PID整定
机器学习算法可以通过分析历史数据和实时反馈来优化PID控制器的参数。例如,强化学习可以用来自动调整PID参数,以实现系统性能的最优化。在这一过程中,算法通过试错的方式学习如何调整PID参数以获得最佳的控制效果。
6.1.2 深度学习在PID控制优化中的潜力
深度学习,特别是神经网络,因其在处理非线性问题和大数据集上的优越性,正逐渐被应用于PID控制系统的建模和参数优化。通过使用深度神经网络,可以构建更为复杂的系统模型,并实现更为精确的PID参数调整。
6.2 PID控制面临的挑战与应对策略
随着工业自动化和智能制造的发展,PID控制技术正面临越来越多的挑战,但同样也伴随着创新的机会。
6.2.1 工业自动化中的新挑战
在高度动态和复杂的工业自动化环境中,传统的PID控制器可能无法满足精确控制的要求。例如,快速变化的工作条件、多变的操作参数和复杂的系统响应都要求PID控制器具有更高的适应性和灵活性。
6.2.2 PID控制技术的创新路径
为应对这些挑战,创新的PID控制技术正在被开发,如自适应PID、模糊PID和预测PID等。这些技术通过引入新的控制策略和算法,使得PID控制器能更好地应对环境变化和系统不确定性。
6.3 探索PID技术的跨学科融合与应用
PID控制技术与其他学科的融合打开了新的应用领域,并为该技术的发展提供了新的视角。
6.3.1 跨学科技术的整合思路
通过将控制理论、信息学、计算机科学以及人工智能等多个学科的原理和技术结合起来,PID控制能够实现更高级的性能。例如,将先进的信号处理技术应用于系统的反馈信号,可以提高控制器对噪声和扰动的抵抗能力。
6.3.2 PID技术在新兴领域的应用展望
在物联网(IoT)、自动驾驶、机器人技术以及生物医学工程等领域,PID控制技术正发挥着重要作用。通过与这些领域的技术相结合,PID技术不仅扩展了应用范围,同时也推动了自身的发展和完善。
PID整定技术的未来充满了无限可能。人工智能和跨学科技术的应用将为传统PID控制器带来前所未有的创新和变革。在应对工业自动化中不断涌现的挑战的同时,我们期待PID控制技术能够在新的应用领域中继续扮演核心角色。
简介:PID控制器是自动化控制领域中用于优化系统性能的算法。z-nPID整定方法和差分进化算法(DE)是提高PID控制器性能的两种关键技术。本压缩包内含相关源码,通过这些代码,开发者可以学习如何实施z-nPID整定,以及如何利用差分进化算法进行PID参数的自动优化。理解这些策略对于提升系统控制的稳定性和响应速度至关重要。






















 5万+
5万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








