Legendre polynomials

最新推荐文章于 2024-02-26 19:50:21 发布

weixin_30802171

最新推荐文章于 2024-02-26 19:50:21 发布

阅读量414

点赞数

原文链接：http://www.cnblogs.com/hiramlee0534/p/5539709.html

版权

LegendreP

In mathematics, Legendre functions are solutions to Legendre's differential equation:

${d \over dx} \left[ (1-x^2) {d \over dx} P_n(x) \right] + n(n+1)P_n(x) = 0.$

In particular, it occurs when solving Laplace's equation (and relatedpartial differential equations) in spherical coordinates.

$legendre1.gif$

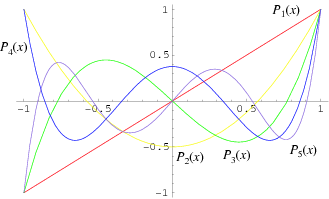
The polynomials may be denoted by P_n(x) , called the Legendre polynomial of order n. The polynomials are either even or odd functions of x for even or odd orders n. The first few polynomials are shown below.

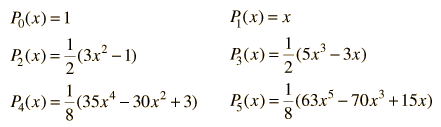
$legendre2.gif$

The general form of a Legendre polynomial of order n is given by the sum:

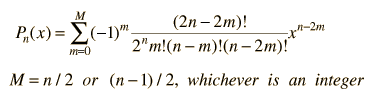
$legendre3.gif$

From the Legendre polynomials can be generated another important class of functions for physical problems, the associated Legendre functions.

转载于:https://www.cnblogs.com/hiramlee0534/p/5539709.html

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。