导出对象_从代数几何到导出代数几何：形变与逼近

我个人总觉得，一个推广的理论不能仅仅是把已知的东西平行地推广到更一般的对象中去，而是能用自身的优势反哺老的理论，就好比复数

之所以值得考虑（以16世纪的眼光），是因为

-系数一元三次方程的求根公式用复数表达十分方便。

接下来我们将比较经典代数几何与导出代数几何，并翻译Toën阐释导出代数几何“逼近”思想的文章，最后我们给出一些导出代数几何反哺经典代数几何的例子。

在上一篇文章中

何通木：从代数几何到导出代数几何：复形的几何​zhuanlan.zhihu.com

我们给出了导出代数几何的研究对象：单纯交换环的单纯局部化

。来看看它比经典的代数几何多出了什么东西。

经典的代数几何：交换环范畴

；

导出代数几何：单纯交换环范畴

，它是一个模型范畴，从而可以像在

中谈论一个复形的预解式一样，来谈论一个单纯交换环的

单纯预解式(simplicial resolution)。这正是导出代数几何比经典代数几何多出的东西： 用预解式来做逼近（标题“形变与逼近”只是互文见义）。

定理（标准单纯预解式，[StP]08N8）：给定任一交换环

，它有典范单纯自由预解式

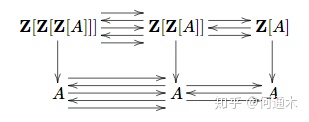
这告诉我们在

里，任何来自于经典代数几何的交换环

可以被自由的单纯预解式逼近，于是在导出代数几何的范畴

里，

与这个自由的东西同伦等价。

---

我将把Toën在 Derived Algebraic Geometry 里一段非常好的关于导出代数几何动机的阐释翻译过来。以下为翻译：

……我们注意到这样一个本原的数学观察。一个给定的数学理论通常致力于研究一类指定的对象：代数几何中的代数簇、拓扑学中的拓扑空间、线性代数中环上的模……一般说来这些对象是非常复杂的（除非这个理论不有趣），但是常常会自然出现一个好对象构成的子类。同它们的名字一样，这些好对象有好的行为，或者至少比一个一般对象的行为要好。在这样的情形中，数学家们相信我们能完全理解这些好对象，并且一般对象可以被好对象进行最佳逼近。这个本原的数学观察在很多具体的例子中出现，以下是两个例子（还有无数其它的例子）：

• （线性代数）令
  是环，我们考虑
  -模。相对于短正合列来说的好对象，就是投射模。对一般的
  -模
  ，它的最佳逼近就是
  的一个投射预解式

• （拓扑学）我们考虑拓扑空间，以及它们的上同调性质。球面是好对象（从上同调的角度）。对于空间
  ，它的最佳逼近就是胞腔逼近，也即一个弱等价于
  的CW复形
  。

这两个例子有很多变体，比如把环上的模替换成阿贝尔范畴中的对象，或者把拓扑空间替换成光滑流形，胞腔逼近替换成柄体分解。这些例子的共通之处就是逼近构造的行为。一个精妙的问题是它们的唯一性：逼近显然在严格意义下不是唯一的（比如上述两个例子中就不是，这是一般现象），我们必须引入新的“等价”的概念，来掌控唯一性以及函子性质。在上面的例子中，这个新概念显然：在第一个例子中就是复形的拟同构，在第二个例子中就是弱同伦等价。我们将在下一段落中看到，引入“等价”的新概念自动地生成了一个更高范畴的、或者更高同伦的现象。这便是很多数学领域中高阶范畴结构普遍存在的一个原因。

导出代数几何是从代数几何中导出的理论（没有一语双关），应用着上面的一般原理，认定好对象是光滑簇、光滑概形以及光滑态射。这里由光滑簇给出的逼近就是第一节提到的代数的单纯预解式由多项式代数给出。总结起来：

• （导出代数几何第一原理）光滑簇，或者更一般地，光滑概形及光滑态射，都是好的。任一不光滑的簇、概形或态射，都可以被替换成由光滑对象给出的最佳逼近。
• （导出代数几何第二原理）簇、概形及态射的逼近，可以用单纯预解式表达出来。单纯预解式必须在弱等价意义下考虑，并且由高阶范畴的或高阶同伦的结构所控制。

基于这两条原理，我们可以抽象出导出概形的一般定义，简单地可以认为结构层现在得是单纯交换环的层，而不是交换环的层。然而，第二原理已经告诉我们导出概形之间的态射是一个更密切的概念，并且必须谨慎定义。

定义（导出概形的第一定义）：一个导出概形是一个对子

，其中

是一个拓扑空间，

是

上的一个单纯交换环层，满足下面两个条件

1. 赋环空间
   是一个概形；
2. 对任意
   ，同伦层
   是概形
   上的拟凝聚层。

关于此定义的一些评论：

• 一个概型
  显然可以视作导出概形，只需令
  为
  的常单纯层。
• 另一方面，一个导出概形
  暗含概形
  ，这被称为是
  的
  截断。
• 一个概型也可视作导出概形
  ，其中
  是
  的任一单纯预解式，也即
  ，
  。我们将看到，导出概形
  等价于
  （就好比模
  的预解式
  拟同构于集中在度
  的
  ）。
• 对导出概形
  ，其截断
  包含了所有的几何。
  上的层
  反映着导出结构，理应被视作额外的幂零函数。层
  类似于分次块
  ，其中
  是概形
  的幂零根，从而是既约子概形
  上的一些层。这是非常好的直观，也正确地将
  视为具有自然的过滤（化身为Postnikov塔），其分次块就是
  。

上面的定义让导出概形成为一个简单的概念，至少第一眼看过去是的。然而，如已经提到的，导出概形之间的态射需要在有意义的方式下谨慎地定义。接下来，我们将解释如何处理导出概形，如何构造及定义它们的无穷范畴，以及如何在实际中更它们打交道……

（翻译结束）

---

所以导出代数几何就是给出了用光滑概形逼近一般概形的正确体系。在导出代数几何中这种逼近理应视作相等（毕竟在

中弱等价就是同构），并且无穷范畴

把两个对象为什么相等记录了下来，这对于定义同伦意义下的极限和余极限有好处。

一个直观的现象就是，对光滑概形成立的结论，理应对任一导出概形成立。

例（[Bh]3.2，3.5）：

（经典版本）对

-代数

，若

自由，那么有Cartier同构：

其中

代表余切复形，

代表de Rham复形。

（导出版本）对

-代数

，有导出Cartier同构：

其中

代表导出de Rham复形。

我们也可以用导出代数几何反哺经典代数几何：

例（[Bh]3.17）：Deligne-Illusie（1987）把局部提升信息粘成导出范畴中的态射从而证明的Hodge退化定理，在导出代数几何中只需简单地使用同伦提升定理即可，并且在光滑的情况下，导出表述退化为经典表述，从而给出了Hodge退化定理的一个导出代数几何证明。

参考文献：

[StP] The Stacks project authors, The Stacks Project, 2019.

[To] Toën, B., Derived Algebraic Geometry, 2014.

[Bh] Bhatt, B., p-adic derived de Rham cohomology, 2012.

在翻译的过程中遇到了个问题，就是数学中的"up to"应该怎么翻译？