怎么判断二阶导数是否异号_「高等数学」给出函数的二阶导函数图形，求该曲线图形拐点的个数...

拐点，又叫做反曲点，从字面意思上来说，拐就是拐弯的意思，顾名思义，指的是改变曲线向上或者向下方向的点，也可以说拐点是使切线穿越曲线的点。

那么拐点和二阶导函数之间有什么关系呢，我们一般说如果某曲线图形函数在拐点有二阶导数，则二阶导数载拐点处异号(正到负或者负到正)或者说不存在。

那么我们一般怎么来求拐点呢，我们往往有如下步骤：

1、求该曲线图形函数的二阶导数。

2、令该曲线图形函数的二阶导数等于零，解出该方程在区间内的实数根，并求出在该区间内二阶导数不存在的根。

3、对于第二个步骤求出来的根或者说二阶导数不存在的点，我们就可以进行观察了，检查二阶导数在该点左右两侧邻近的符号，当两侧的符号相反时，很明显，该点满足异号这个条件，就说明该点是拐点，反之，该点不是拐点。

话不多说，我们来看一道实际例题，这道题目是2015年考研数学一的第一题，难度不是很大，只需要判断异号的个数即可。

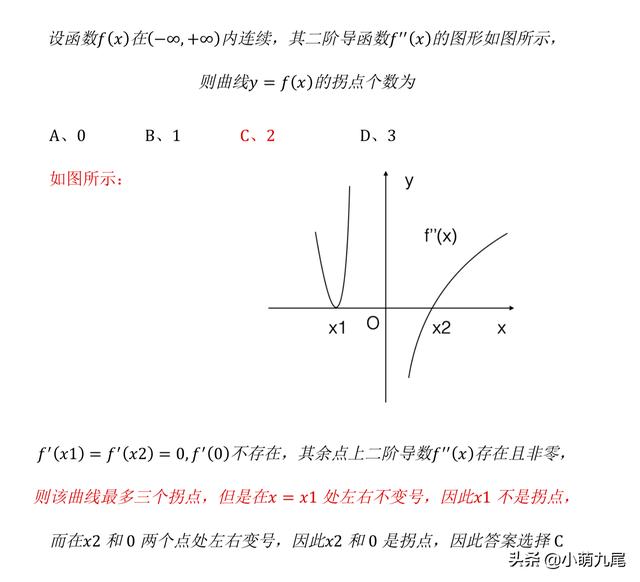
图一

如图所示，这道题已经很友善了，直接给出二阶导函数f''(x)的图形，直接让我们求拐点。

那我们就可以直接得到一些信息，在x1点和x2点两个点的时候，该二阶导函数的值为零。

我们可以观察，得到x1左右两侧同号，所以x1不是拐点，排除。

x2左右两侧异号，所以x2是拐点，选择。

但是我们要注意，这里还有一个情况，那就是0这个点，由前面的信息可得，在0这个点处，二阶导函数不存在，并且点0左右异号，所以0也是一个拐点。

综上所述，这道题目的答案就应该选C。

总结一下，遇到这种题目，只需要掌握拐点的概念即可，难度不大，仔细一点就肯定没什么问题，关键还在于二阶导数等于零和二阶导数不存在求出的点可能是拐点，最后再用左右是否同号还是异号来进行判断即可。