【opencv】18.数字图像一阶导数、二阶导数的数学原理

以下内容都是从这篇博客中摘抄的，中间写了一些自己的理解和疑问。

---

一阶导数求导过程：

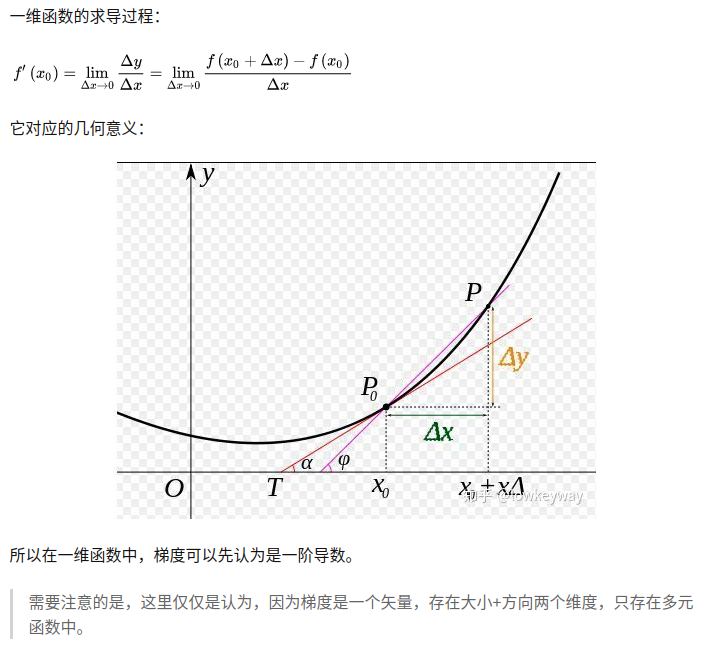
二阶导数求导过程：

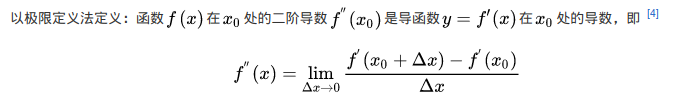
用数学公式表达一阶微分（不同于连续函数的无限趋向于0的 [公式] ，数字领域最小单位为1）：
摘自：第三章 灰度变换与空间滤波-（六）锐化空间滤波器之基础

从上面两个公式可以看出：

• 对图像的某元素求一阶导数，就是用相邻像素的像素值减去这个像素的像素值。不过上面只展示了一维的x，另一维的y没写出来，也就是y不变时，该像素的右边像素的像素值减去该像素的像素值。这是检测横向的。同理，也可以检测纵向的，还有斜线的，这就涉及到下面要讲的二维图像的梯度了。
• 对图像的某元素求二阶导数，就是用前一个像素的像素值+后一个像素，再减去2倍的这个像素。

但是，图像是二维的，有x,有y，你要检测的特征都可以使用一阶导数的最大值(即梯度)来检测，对于二维图像，梯度是一个向量，他的方向指向你要检测的方向，而你要检测的方向是由算子来指定的。

---

原文链接用梯度（一阶微分）实现图像锐化

看清楚，上面的3x3是图像的一小块，并不是卷积核，也不是算子模板。

卷积核与算子：

可以参考下这篇博客。

卷积核并不是算子，因为卷积核，顾名思义，就是卷积操作(加权和)。
算子不止进行卷积，还得进行额外的运算，即求梯度，求梯度的模就用到了平方和后在开方的操作，并且一个算子是两个模板(每个模板就像卷积核一样的划窗)，分别表示梯度的两个方向gx和gy。并且，卷积核的总和为1，而算子的每个模板的总和都为0。

---

下面内容摘自【第三章 灰度变换与空间滤波-（六）锐化空间滤波器之梯度】

Sobel算子的数字中间那一行或者那一列比其他的行或列大，可能是因为最靠近中心点像素吧。
以sobel算子为例，本来中间那一行应该是0.5 0 0.5，但是却定为-2 0 2，是因为乘以一个系数(这里乘了4)并不影响，因为图像的每一个像素都是相同的处理，所以并不影响。

Sobel算子：