求均值方差_三个视频搞定：离散性随机变量的均值、方差

● 本文适合高二下学期、高三一轮复习的同学阅读。先看视频再看文字，看视频时注意利用暂停，想清楚每一步变形的依据。

01

离散型随机变量的均值

视频讲解

1、离散型随机变量的均值

2、均值的性质

若Y＝aX＋b，其中a，b为常数，X是随机变量，

①Y也是随机变量；

②E(aX＋b)＝aE(X)＋b。

3、两点分布、二项分布的均值

(1)两点分布：若X服从两点分布，则E(X)＝p    .

(2)二项分布：若X～B(n，p)，则E(X)＝ np

两点分布与二项分布辨析

①相同点：一次试验中要么发生要么不发生.

②不同点：随机变量的取值不同，两点分布随机变量的取值为0,1，二项分布中随机变量的取值X＝0,1,2，…，n.；试验次数不同，两点分布一般只有一次试验，二项分布则进行n次试验.。

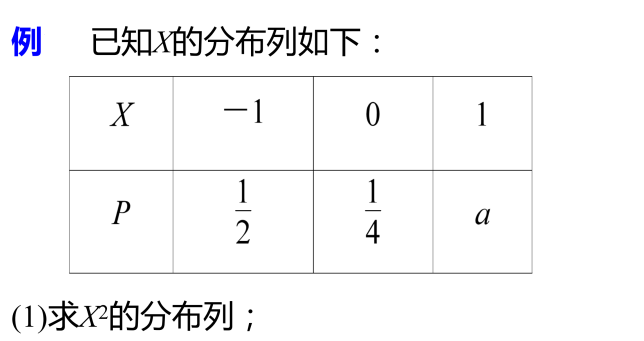
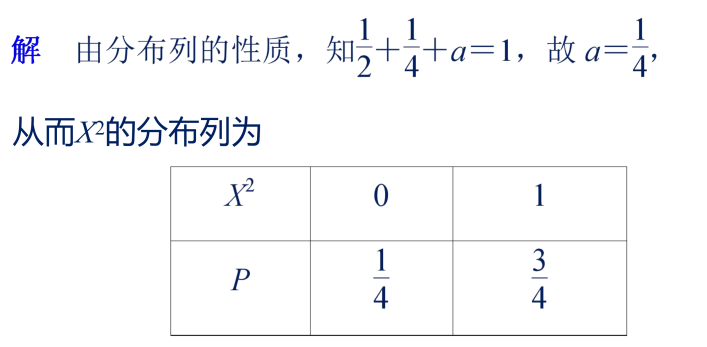
4、利用定义求随机变量的均值

例　袋中有4个红球，3个白球，从袋中随机取出4个球.设取出一个红球得2分，取出一个白球得1分，试求得分X的均值.。

求随机变量X的均值的方法和步骤

(1)理解随机变量X的意义，写出X所有可能的取值.

(2)求出X取每个值的概率P(X＝k).

(3)写出X的分布列.

(4)利用均值的定义求E(X)。

5、运用离散型随机变量均值性质解题

若给出的随机变量ξ与X的关系为ξ＝aX＋b，a，b为常数.一般思路是先求出E(X)，再利用公式E(aX＋b)＝aE(X)＋b求E(ξ).也可以利用X的分布列得到ξ的分布列，关键由X的取值计算ξ的取值，对应的概率相等，再由定义法求得E(ξ).。

02

离散型随机变量的方差、标准差描述偏差

视频讲解

6、方差、标准差

均值体现了随机变量取值的平均大小，在两种产品相比较时，只比较均值往往是不恰当的，还需比较它们的取值偏离于均值的平均程度，即通过比较方差，才能准确地得出更恰当的判断.。这就是学习方差的意义。

7、两点分布、二项分布的方差

03

数据散布特征为何选方差？何为自由度？

(本文图片与视频来自于网络，仅供学习交流用，若有侵权，请联系删除。)

人生有缘才相遇 扫码相识更有趣

微信号 :rong19711107 

公众号：周老师松果数学

● 扫码联系我

zlssgsx