一:对数频率特性曲线(波德图-Bode图)
Bode图由对数幅频特性和对数相频特性两条曲线组成。⒈波德图坐标(横坐标是频率,纵坐标是幅值和相角)的分度:
1)横坐标分度(称为频率轴):它是以频率w的对数值logw进行线性分度的。但为了便于观察仍标以w的值,因此对w而言是非线性刻度。w每变化十倍,横坐标变化一个单位长度,称为十倍频程(或十倍频),用dec表示。类似地,频率w的数值变化一倍,横坐标就变化0.301单位长度,称为“倍频程”,用oct表示。如下图所示:


2)纵坐标分度:对数幅频特性曲线的纵坐标以L(w)=20logA(w)表示。其单位为分贝(dB)。直接将20logA(w)值标注在纵坐标上。
相频特性曲线的纵坐标以度或弧度为单位进行线性分度。一般将幅频特性和相频特性画在一张图上,使用同一个横坐标(频率轴)。当幅制特性值用分贝值表示时,通常将它称为增益。幅值和增益的关系为:增益=20log(幅值)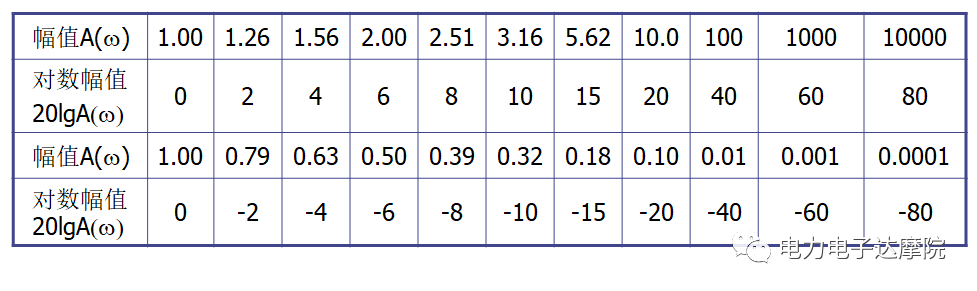
二:典型Bode图
1. 比例环节 G(s)=K
G(jw)=K幅频特性:A(w)=K;相频特性:ψ(w)=0
2. 积分环节 G(s)=K/s
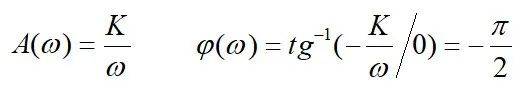

3. 惯性环节
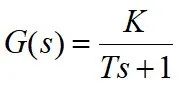
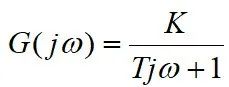
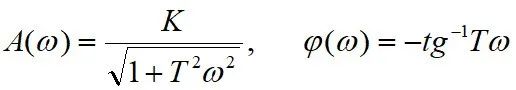

4. 振荡环节


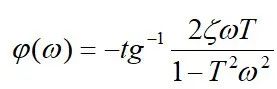
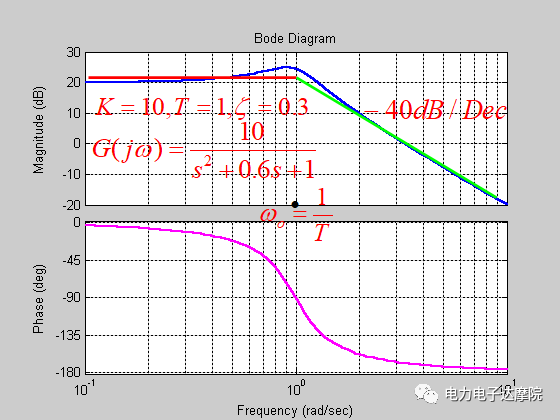
对A(w)求导并令等于零,可解得A(w)的极值对应的频率wp:
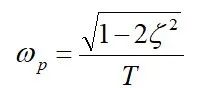
该频率称为谐振峰值频率,可见当ζ=0.707时,wp=0。
当ζ>0.707时,无谐振峰值
当ζ<0.707时,有谐振峰值:

因此在转折频率附近的渐近线依不同阻尼系数与实际曲线可能有很大的误差。








 本文深入探讨了自动控制系统的二阶振荡环节,详细解析了对数频率特性曲线(波德图),包括横纵坐标的分度规则。重点讲述了谐振峰值频率wp的计算,指出当阻尼系数ζ=0.707时,wp=0,揭示了ζ对谐振峰值的影响。
本文深入探讨了自动控制系统的二阶振荡环节,详细解析了对数频率特性曲线(波德图),包括横纵坐标的分度规则。重点讲述了谐振峰值频率wp的计算,指出当阻尼系数ζ=0.707时,wp=0,揭示了ζ对谐振峰值的影响。
















 7280
7280

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








