自动控制原理——频域分析

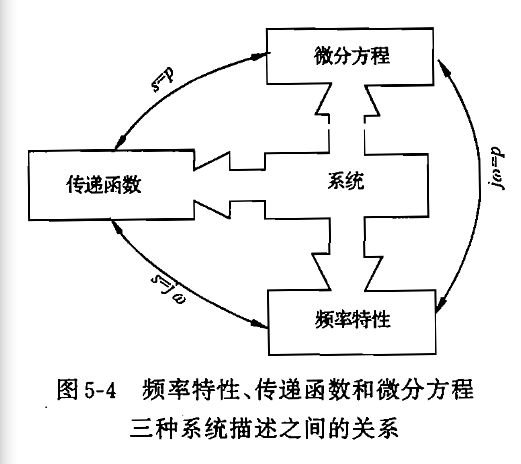
频域分析法

①频域特性可以通过分析法和实验法获得，并可以用多种形式的曲线表示，因而系统分析和控制器设计可以应用图解法进行

②频域特性物理意义明确，对于一阶和二阶系统，频域性能指标和时域性能指标有明确的对应关系；对于高阶系统，可以建立近似的对应关系

③频域设计可以兼顾动态响应和噪声抑制两方面的要求

④频域分析法不仅适用于线性定常系统，还可以推广应用于某些非线性控制系统

几何表示

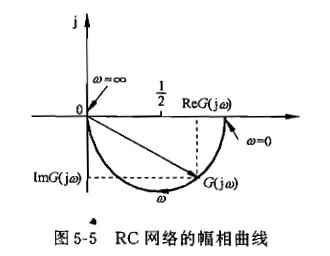
幅相频率特性曲线：又称为幅相曲线或极坐标图，以横轴为实轴、纵轴为虚轴，构成复数平面,绘制w从0到+∞的曲线

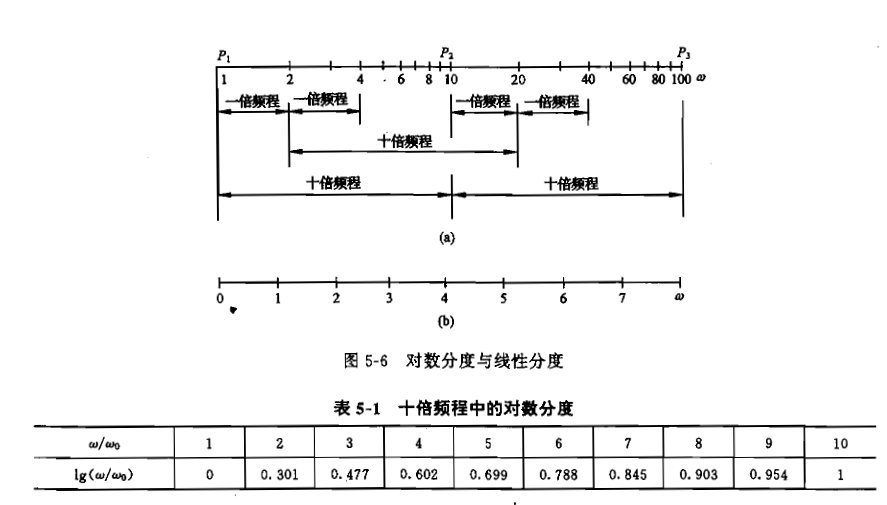
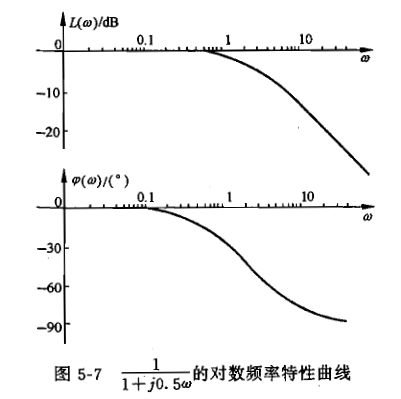
对数频率特性曲线：又称为伯德曲线或伯德图，横坐标为lgw，单位为rad/s，纵坐标为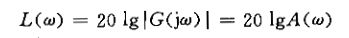单位为dB，

对数相频曲线的纵坐标为φ(w)，单位为°，由此构成的坐标系称为半对数坐标系

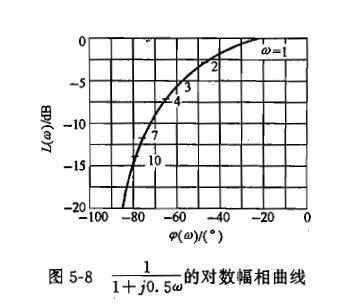
对数幅相曲线：又称为尼科尔斯曲线或尼科尔斯图，纵坐标为L(w)，单位为dB， 横坐标为φ(w)，单位为° ，w为参变量

典型环节

①最小相位环节

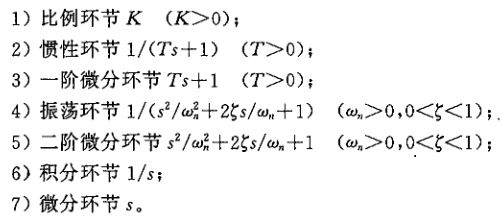
②非最小相位环节

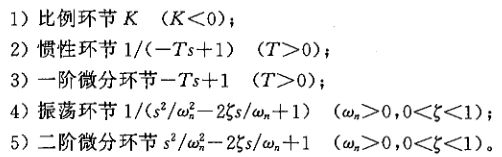
除比例环节外，最小相位环节和非最小相位环节的区别在于开环零极点的位置（非最小相位环节在s右半平面，最小相位环节在s左半平面）

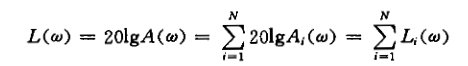
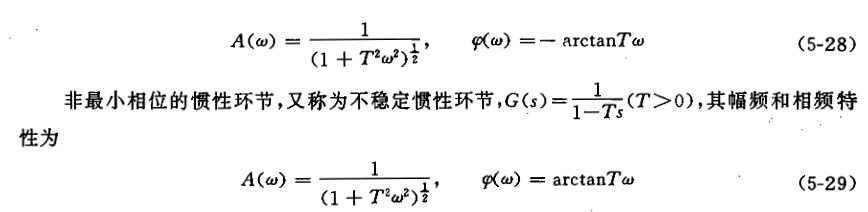
①最小相位环节和对应的非最小相位环节（比例环节、惯性环节、振荡环节、一阶微分环节、二阶微分环节）幅频特性相同，相频特性符号相反，幅相曲线关于实轴对称；对数幅频曲线相同，对数相频曲线关于0°对称。

②传递函数互为倒数的典型环节（最小相位典型环节中的积分环节和微分环节、惯性环节和一阶微分环节、振荡环节和二阶微分环节，非最小相位环节中传递函数互为倒数的典型环节）对数幅频曲线关于0dB对称，对数相频曲线关于0°线对称

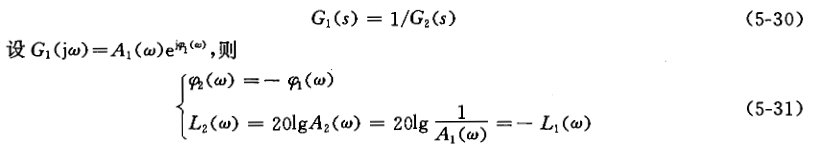
③振荡环节和二阶微分环节

振荡环节

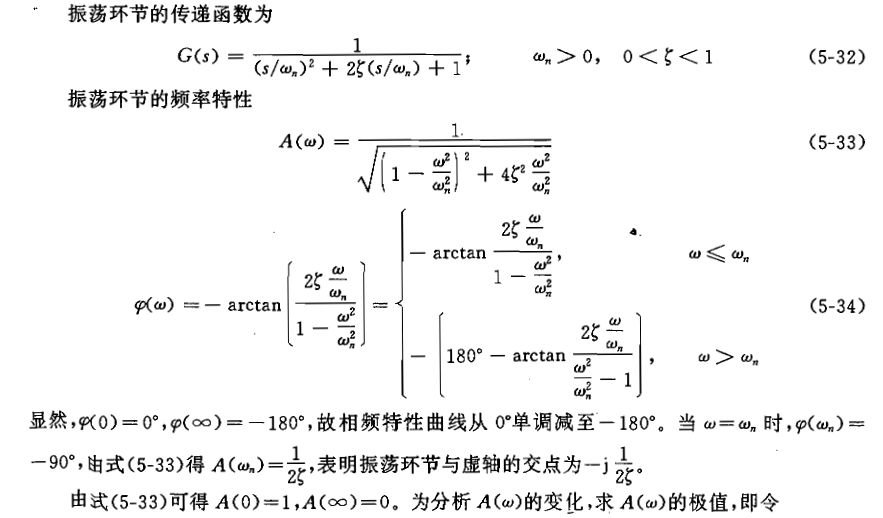
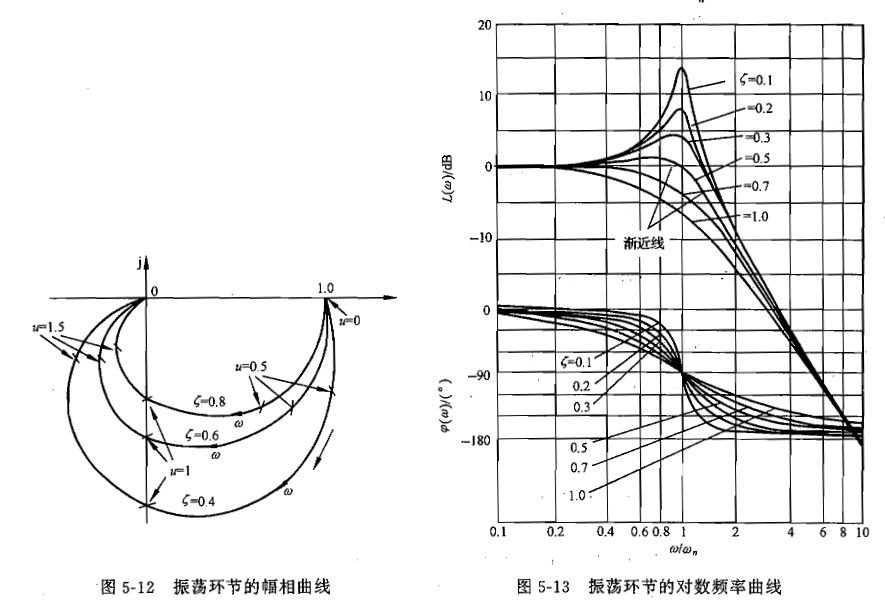
二阶微分环节——传递函数为振荡环节的倒数

w∈(wr,∞)时，A(w)单调递增

④对数幅频渐进特性曲线：用低频和高频渐近线近似表示对数幅频曲线（惯性环节、一阶微分环节、振荡环节、二阶微分环节）

惯性环节的对数幅频特性