线段中点到另一直线距离最短_「解题策略」最值系列之将军饮马（一）

“白日登山望烽火，黄昏饮马傍交河”，这是唐代诗人李颀《古从军行》里的一句诗。而由此却引申出一系列非常有趣的数学问题，通常称为“将军饮马”。

01

什么是将军饮马？

【问题描述】

如图，将军在图中点A处，现在他要带马去河边喝水，之后返回军营，问：将军怎么走能使得路程最短？

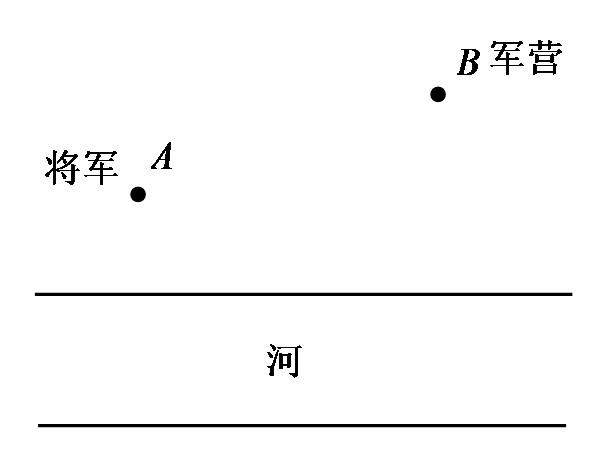
【问题简化】

如图，在直线上找一点P使得PA+PB最小？

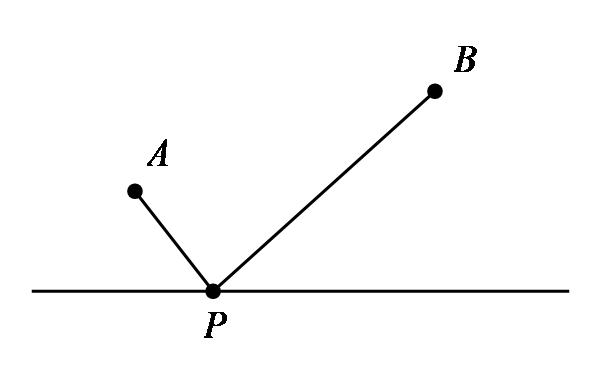
【问题分析】

这个问题的难点在于PA+PB是一段折线段，通过观察图形很难得出结果，关于最小值，我们知道“两点之间，线段最短”、“点到直线的连线中，垂线段最短”等，所以此处，需转化问题，将折线段变为直线段．

【问题解决】

作点A关于直线的对称点A'，连接PA'，则PA'=PA，所以PA+PB=PA'+PB

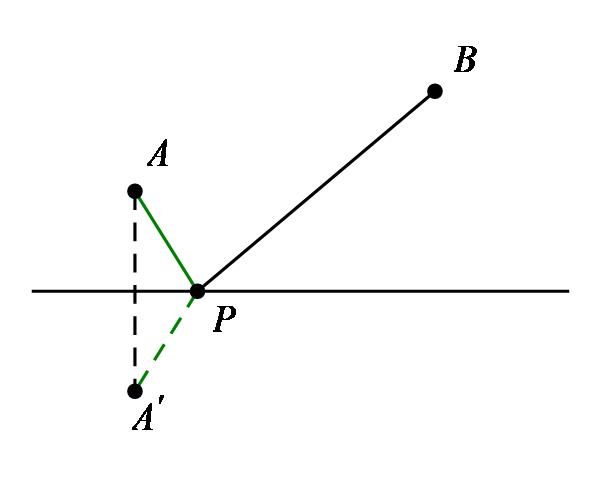
当A'、P、B三点共线的时候，PA'+PB=A'B，此时为最小值(两点之间线段最短)

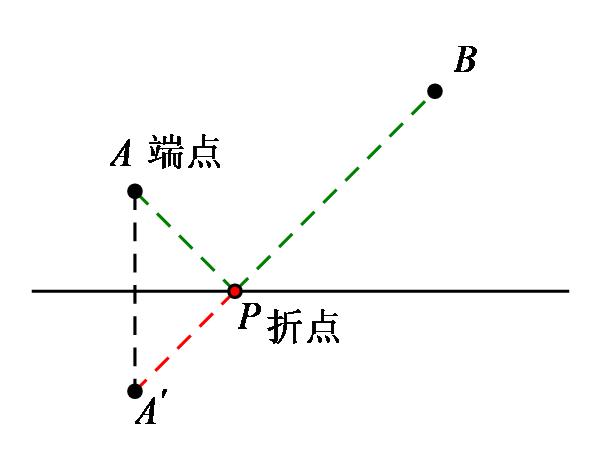
作端点(点A或点B)关于折点(上图P点)所在直线的对称，化折线段为直线段．

02

将军饮马模型系列

“一定两动”之点到点

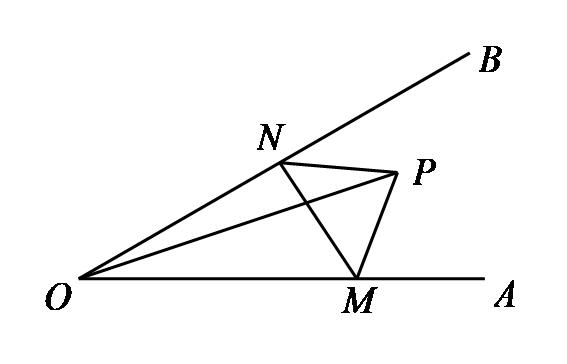
在OA、OB上分别取点M、N，使得△PMN周长最小。

【此处昨日推文配图错误，正确图如下】

此处M、N均为折点，分别作点P关于OA(折点M所在直线)、OB(折点N所在直线)的对称点，化折线段PM+MN+NP为P'M+MN+NP''，当P'、M、N、P''共线时，△PMN周长最小。

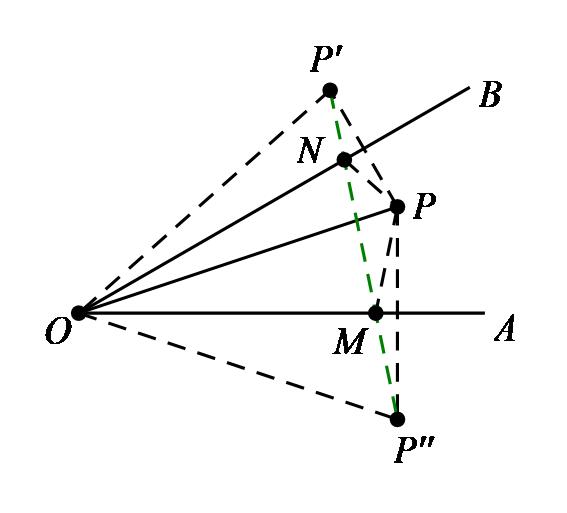
【例题】如图，点P是∠AOB内任意一点，∠AOB=30°，OP=8，点M和点N分别是射线OA和射线OB上的动点，则△PMN周长的最小值为________．

【分析】△PMN周长即PM+PN+MN的最小值，此处M、N均为折点，分别作点P关于OB、OA对称点P'、P''，化PM+PN+MN为P'N+MN+P''M．

当P'、N、M、P''共线时，得△PMN周长的最小值，即线段P'P''长，连接OP'、OP''，可得△OP'P''为等边三角形，所以P'P''=OP'=OP=8．