三角形周长最短问题_模型研究 | 再谈“将军饮马”问题（综述）

推荐阅读

• 模型研究 | 最值之将军饮马、将军遛马、将军过河

• 解题研究｜名师之作：几何最值问题大一统

• 初中数学必会之模型解题法

• 归类提升 | 初中数学常见几何模型全解析

• 名师系列 | 经典几何模型之“阿式圆”

• 学会此6大类模型，轻松秒杀初中数学相似问题

1.问题的历史背景： “将军饮马问题”

传说早在古罗马时代，亚历山大城有一位精通数学和物理的学者，名叫海伦。一天，一位罗马将军专程去拜访他，向他请教一个百思不得其解的问题：如图，将军从军营A出发先到河边饮马，再去同侧的B地开会，应该怎样走才能使路程最短？这个问题的解决并不难，据说海伦略加思索就解决了它，展现了他的个人智慧。从此，这个被称为“将军饮马”的问题广为流传。

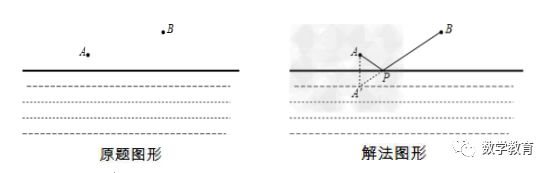
2.究其本质，巩固模型。

如图，A、B两点分别表示两幢大楼所在的位置，直线n表示输水总管道，直线b表示输煤气总管道。现要在这两根总管道上分别设一个连接点，安装分管道将水和煤气输送到A、B两幢大楼，要求使铺设至两幢大楼的输水分管道和输煤气分管道的用料最短。图中，点A′是点A关于直线b的对称点，A′B分别交b、a于点C、D；点B′是点B关于直线a的对称点，B′A分别交b、a于点E、F．则符合要求的输水和输煤气分管道的连接点依次是(    )

 A  F和C     B  F和E     C  D和C       D  D和E

评析：虽然图形略有改变，但是究其本质，它仍然是我们已建立的基本模型。根据模型易得：输水分管道的连接点是点B关于a的对称点B′与A的连线的交点F，煤气分管道的连接点是点A关于b的对称点A′与B的连线的交点C，故选A。此例关键是抓住模型的本质特征，进一步巩固已经建立的模型，从而达到学以致用的效果。

3.一“模”多变，触类旁通。

通过以上模型的建立，我们把题目做一些变式。

模型变式------ 两定点到直线上一动点的线段距离和最短问题

变式①：“模型”在三角形中

如图，等边△ABC的边长为6，AD是BC边上的中线，M是AD上的动点，E是AC边上一点，若AE=2，求EM+BM的最小值_____。

评析：此例是求两个定点到直线上一个动点距离和最短问题。只要抓住模型的本质特征，作出图形，找到点M的位置并不困难。例如：解法(一)图形，然后利用等边三角形的特殊性质，结合勾股定理的知识，再求出这条线段CE’的长度。也可用解法(二)图形，先利用模型，再根据“点到直线的距离最短”并结合勾股定理来考虑解题方案。由此