图形大小_PS图形复制——等距复制、旋转复制、大小变换复制

PS中图形复制是很常见的事，可能不同人的习惯可能会用不同的方法。这里糖糖主要讲的是图形的一些等距复制、旋转复制、大小变换旋转复制，相信看过本篇文章之后你也可以通过图形的不同需要的复制做一些很不错的图案哦~

糖糖先在PS里用钢笔工具绘制了一个绿叶，下面多数以此为例，当然大家可以使用自己需要的不同形状来做练习~

按alt键拖动图形可复制

要注意使用选择工具的时候，顶部属性栏要勾选“自动选择”，那样鼠标放到哪个图形上就会自动选择哪个图层。

大家可以把鼠标放到叶子上，同时按alt键会看到鼠标变成一个黑色箭头下面是一个白色箭头，这就代表复制的意思，可以拖动叶子图形移动到任何地方，就等于移动复制了一层，如下：

复制的时候按shift+alt，可以水平或垂直复制对齐图形

如果想要平行移动复制的话，按alt复制的时候不松手同时也要按shift，即可强制水平对齐或垂直复制对齐第一个图形。

糖糖觉得叶子图形平行复制可能显示效果不明显，下面就用圆角矩形形状为例子，在水平和垂直方向都做了移动复制。

具体可以打开标尺拉辅助线，根据辅助线就可以明显的看出：垂直方向和水平方向的移动复制都是对齐第一个图形的。

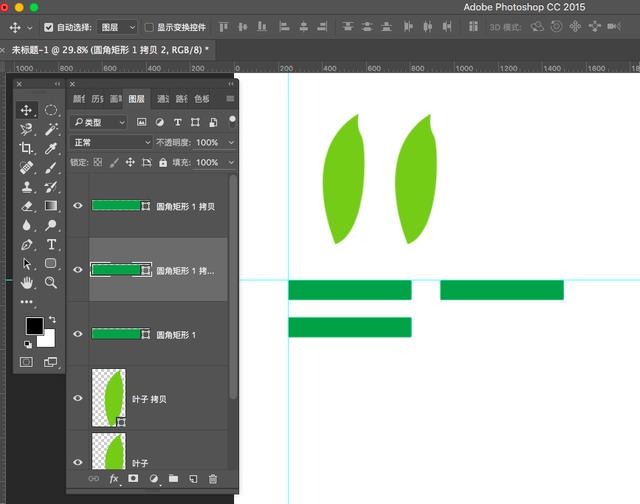
等距离水平复制和偏移复制

有了上面的基础，下面做等距离复制图形就会更容易理解了，下面还以绘制的叶子为例。

先绘制叶子图形，接下来执行自由变换，快捷键ctrl+T，然后随意移动位置后确定即可。

最后三键ctrl+shift+alt+T进行叶子形状的再制，多执行几次三键+T，是偏移复制的效果，如下：

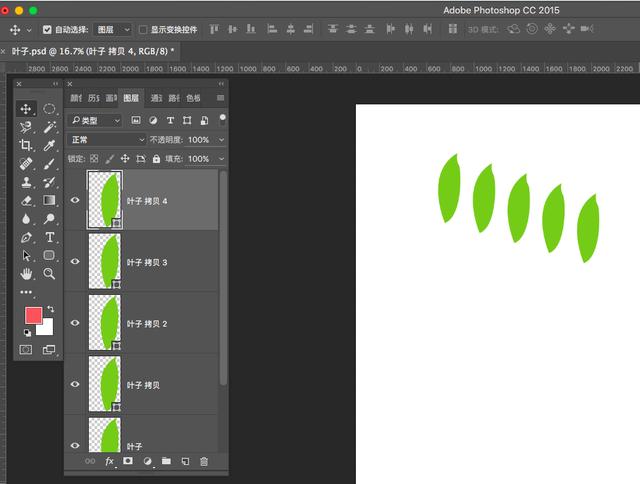
由于自由变换移动叶子的时候是自由移动的，没有按shift进行强制水平方向的移动，所以多次三键+T后的效果上面看起来就是偏移复制且等距离的。

若要水平方向等距离移动复制，自由变换移动的时候要按shift，最终结果复制出来就是水平对齐且等距离的，如下：

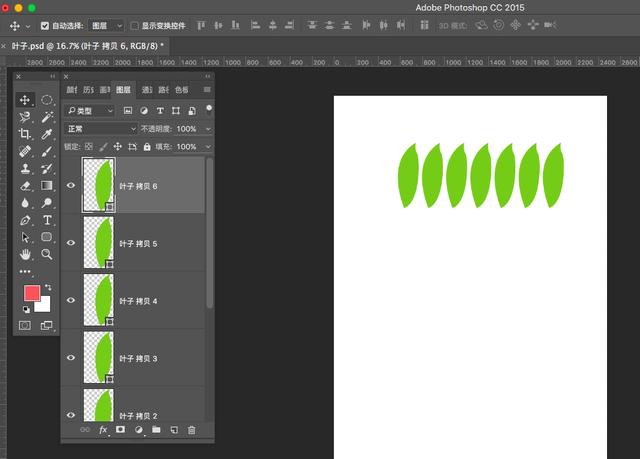
这里是水平移动复制的，垂直方向的移动等距离复制方法也是一样的哟~

旋转复制

其实旋转复制和水平复制方法是一样的。选择叶子图形，自由变换ctrl＋T，按alt键可以移动叶子的中心点至合适的地方，如下图：

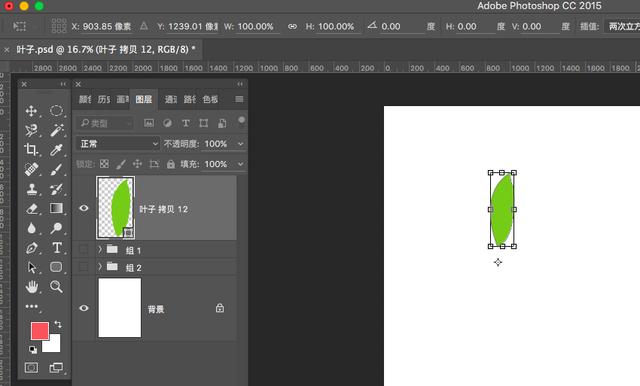
此时自由变换顶部属性栏有个旋转的属性，可以根据需要输入旋转的数值参数，这里糖糖暂且就随便输入了15度进行旋转，如下：

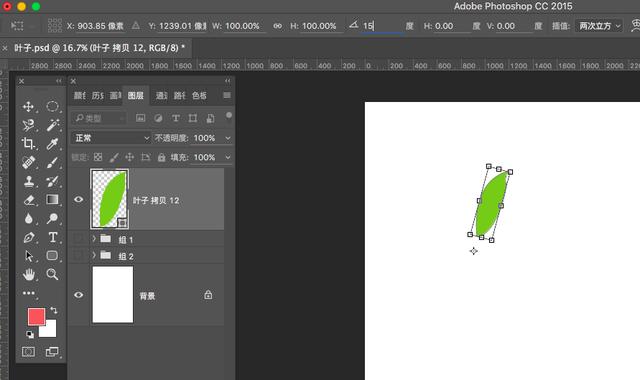
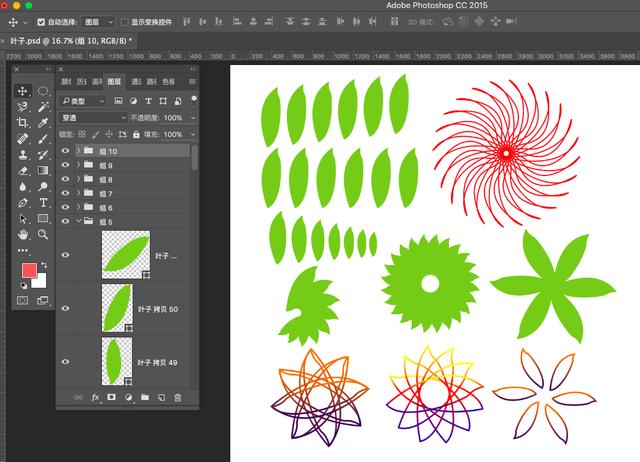
角度由你的需要选择设置哦，最后三键ctrl＋shift＋alt＋T进行再制，多执行几步直到自己需要的结果，糖糖的图形旋转复制结果如下：

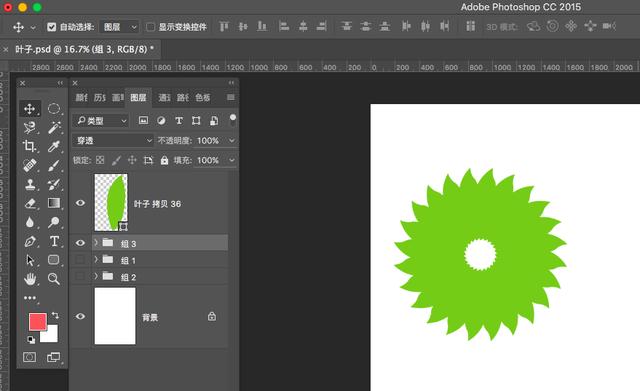
旋转缩小、放大复制

其实同旋转复制方法也是一样的，不过旋转的同时要做放大或缩小的命令而已。

对叶子执行自由变换ctrl＋T，按shift适当等比例缩小叶子，同时按alt移动中心点，设置旋转数值。

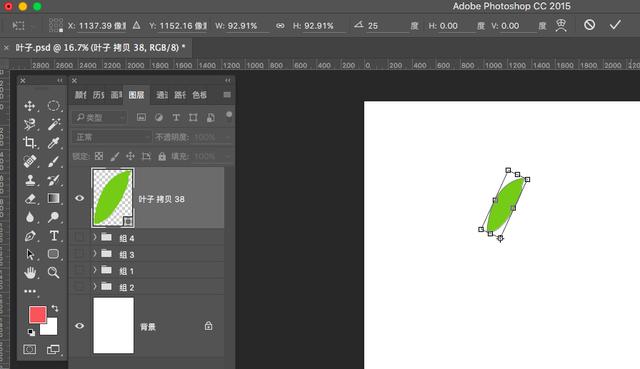
接下来三键＋T，然后多执行几步再制的命令，效果如下：

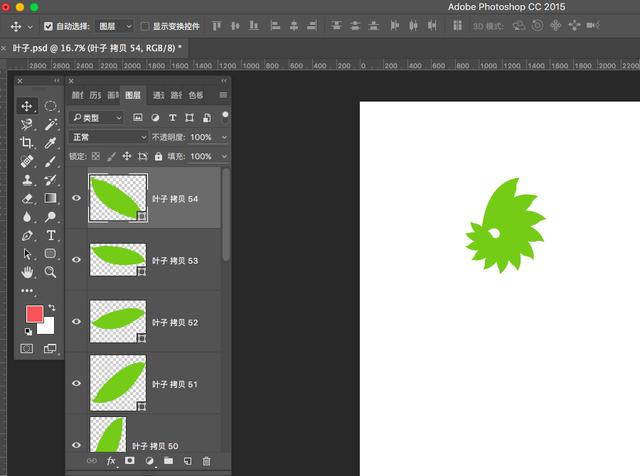
水平方向缩小复制也是可以的，当然放大也是可以的，这个主要根据需要来操作。

---

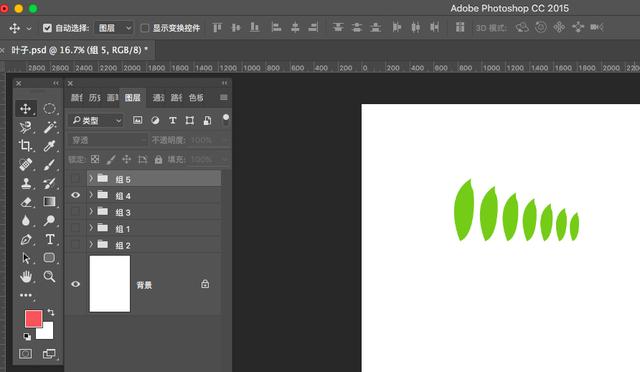
通过上面一些复制，相信大家都了解了PS中图形的水平或垂直等距离复制、旋转复制的操作，其他的主要掌握方法可以自己根据需要灵活运用就好。

大家可以用线条、图形描边也都是可以的，不同的旋转角度也会有不同的效果，大家可以玩起来哦~