回归平方和怎么计算_[机器学习] 最实用的算法：回归

朴素贝叶斯，决策树，支持向量机等都是属于离散型的监督分类，本文要讲的是连续型监督分类：回归（regression）

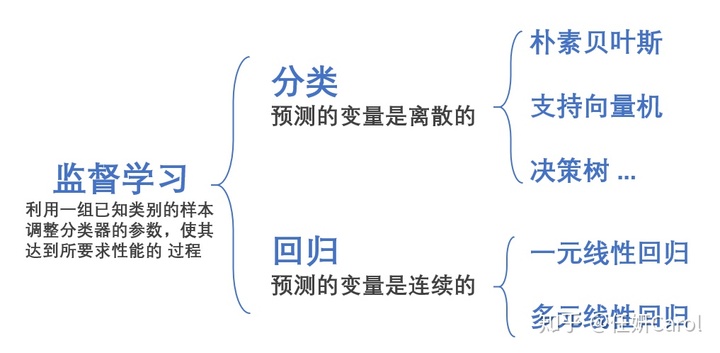
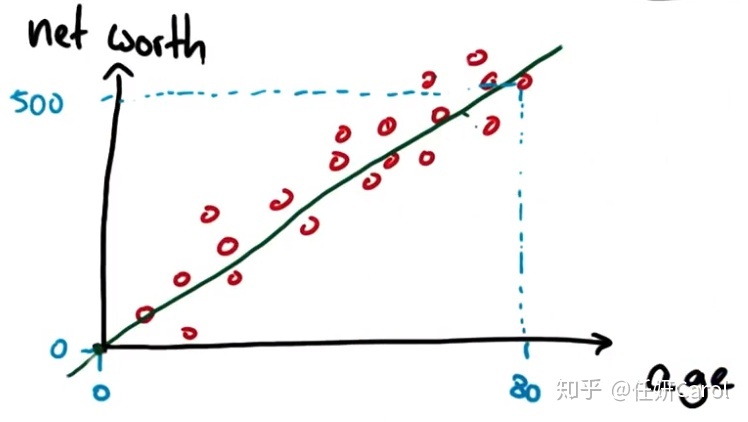
其实回归太常见不过了，我们学过的一元一次方程，x作为自变量，y作为因变量，就是一个连续型的回归，例如下图的年龄和收入的关系

---

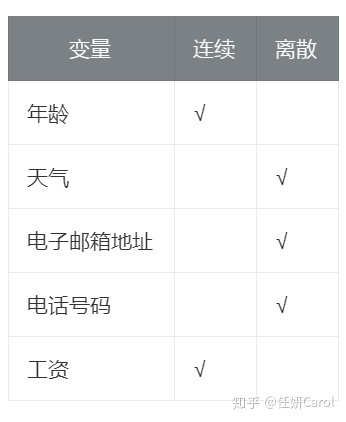
连续还是离散

连续和离散这个概念也是非常简单的，离散变量指变量值可以按一定顺序一一列举，通常以整数位取值的变量。而连续则不可以，下面有个简单的图表可以让你更直观了解这个概念：

线性回归

不同于小时候我们学的一元一次方程，回归可能是多元的，有很多不同的变量，如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析，公式如下：

那么这个公式中x前面有很多系数，这些系数是怎么求得的呢？就是通过线性回归最常用的方法：最小二乘法，这个方法简单了说就是我们通过使拟合得到的预测数据与实际数据之间的误差的平方和是最小的而得出来得式子（这个在下一部分也会讲到）

打开scikit-leant 线性模型我们可以看到线性回归的代码示范，之后我们如果要使用线性回归的模型的时候，就可以用这里的示范来帮助我们完成自己的代码：

如果想要知道线性回归的一些参数，比方说斜率、截距、R²值，可以用以下的代码：

#斜率
reg.coef_

#截距
reg.intercept_

#计算test数据的R²
reg.score(ages_test,net_worths_test)

#计算训练数据的R²
reg.score(ages_train,net_worths_train)

误差

任何的预测都是存在误差的，我们在用线性回归的模型对数据进行了处理之后，也想知道最后得到的这个式子是不是真的拟合的很好，那么就需要看看误差有多少了

显然，这个值是可以有正有负的，那么所有的数据的误差都计算出来相加，有可能那些正正负负的值相互之间消掉了，所以不能看出真正的误差大不大。 因此我们在决定误差的时候，最好是使用所有误差的绝对值的和，或者所有误差的平方和。

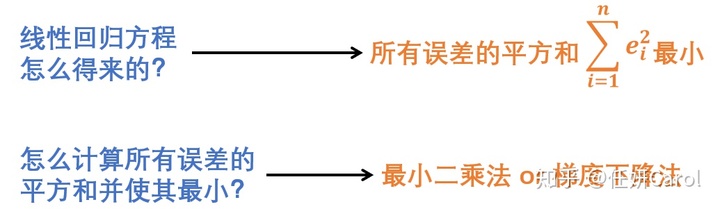
线性回归模型最终选择了所有误差的平方和这一指标，也就是说我们需要找到一些w，使得所有误差的平方和最小

那么问题又来了，怎么才能计算出所有误差的平方和最小呢 ？总共有两种比较常见的方法，分别是最小二乘法和梯度下降法（如果曾经学过ANdrew Ng的机器学习的同学应该对这种方法很熟悉吧~）（对这两种方法感兴趣的同学可以看我的另一篇文章[机器学习] 线性回归中的最小二乘法和梯度下降法比较

R²

所有误差的平方和最小并不是一个完美的评估拟合好不好的方法，因为只要稍微一想，我们就知道数据越多，那么计算出来的平方和肯定越大。只有3个数据的平方和比不过有30000个数据的平方和，但是并不代表30000个数据的拟合效果不好。 是时候认识真正的评估指标了：R² R²是很好的一个评估拟合效果的指标，与数据的多少没有关系，从下面的公式也可以看得出来：

---

你的赞是对作者莫大的支持哦~

如果你想看其他的关于机器学习的一些知识，可以关注我的知乎专栏，我是一个机器学习小白，初学者总会遇到各种各样的困难，我会从初学者的角度把每一个坑都给你仔仔细细的讲明白咯~

更多内容请看本专栏目录

任妍Carol：机器学习小白笔记目录​zhuanlan.zhihu.com