半圆阴影_此题求阴影部分面积，很多人不知从何处动笔，正确分割图形是关键...

各位朋友，大家好！今天是2020年9月10日星期四，数学世界将继续为大家分享小学各年级的数学竞赛试题以及数学思考题。今天我们讲解一道有关求阴影部分面积的图形题，此内容属于小学数学中的一类组合图形题。此题对于多数学生来说是有较大难度的，属于小学数学中的思维拔高题。数学世界在此分析与解答这些题目，希望能够激发学生们的学习数学的兴趣，并且给大家的学习有一些帮助！

例题：(小学数学思考题)如图所示的图形是由一个边长是10厘米的正方形和一个直径是10厘米的半圆组成，其中P点是半圆上的中点，点Q是正方形的边BC的中点，求阴影部分的面积是多少平方厘米？(取π=3.14)

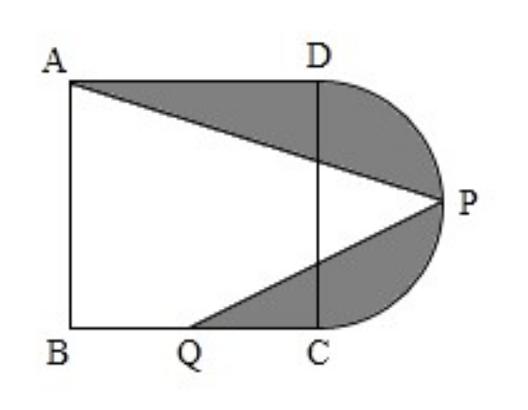
这道题要求的是阴影部分的面积，但阴影部分并不是一个规则图形，所以不能够运用常见图形的面积公式直接解答，只能根据具体情况，考虑采用分割图形法来解决问题。很多学生看完此题后就感觉图形很奇怪！他们完全不知道从何处开始动笔，对于这样的题型，他们可能很少见过吧。接下来，数学世界就与大家一起来完成这道例题吧！

分析：根据条件，阴影部分并不是一个规则图形，考虑采用分割图形法。可以连接PB，则可以看出阴影部分的面积等于图中正方形与半圆的面积之和减去空白部分的两个三角形的面积。下面，我们就来想办法求出三角形PAB和三角形PBQ的面积。

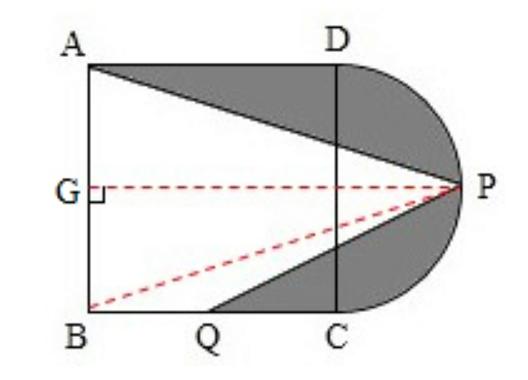
因为P点为半圆周的中点，作出三角形PAB的高PG，根据图形的对称性可以得知G是AB的中点，所以PG的长度为10+10÷2=15厘米，所以三角形PAB的面积可以求得。因为Q点为正方形的边BC的中点，所以三角形PBQ的底和高都可以求出，于是它的面积也可以求出，于是问题得到解决。下面，我们就按照以上思路解答此题吧！

解答：由题意可知，正方形和半圆的面积之和是：

10×10+3.14×(10÷2)^2÷2

=100+39.25

=139.25(平方厘米)

连接PB，作出三角形PAB的高PG，

根据图形的对称性可以得知G是AB的中点，

所以PG的长为10+10÷2=15(厘米)

三角形PAB的面积是：

10×15÷2=75(平方厘米)

因为Q点为正方形的边BC的中点，

所以PG的长为10÷2=5(厘米)

三角形PBQ的面积是5×5÷2=12.5(平方厘米)

则阴影部分的面积是：

139.25-75-12.5=51.75(平方厘米)

答：阴影部分的面积是51.75平方厘米。

(完毕)

这道题主要考查了三角形、正方形和圆的面积公式的综合应用。解答此题的关键是：连接BP，找出两个白色三角形的高，求出空白部分的面积，这也是此题的难点所在。温馨提示：朋友们如果有不明白之处或者有更好的解题方法，欢迎大家在下面留言讨论。