本文报道了SAP全球裁员事件，特别是中国区上海的裁员情况，并提及了外企裁员潮。同时，文章还涉及了一个关于LeetCode面试题的问题，涉及如何在满足员工喜好座位安排的条件下，计算最多能参加会议的员工数量，利用拓扑排序和内向基环树的概念进行分析。
SAP 裁员
最新消息，SAP 宣布全球裁员，中国区（上海）裁员约 1500 名员工。
SAP 也是最早进入 965WLB（work–life balance，工作与生活平衡）名单的外企之一。
加上前几天的特斯拉中国区大裁员，目前已经有多家外企官方宣布裁员，亚马逊魔咒还在继续。
昨天说到，特斯拉给出了 N+3 的赔偿方案，算是不幸中的万幸。
如今 SAP 的赔偿方案也出炉了：
赔偿 N+4，公司假正常折现，年假双倍折现，股票也是全部折现，社保交到 5 月底。
怎么说呢，明明是不幸的消息，但是我却看别人被裁员看出了拆迁的感觉 🤣🤣
东方大国的企业们，N+1 都拿不到，你们这些外来客动不动就 N+3、N+4 的，大家快来一起骂外企们恶意赔偿
...
回归主线。
做一道和「面试笔试」暂无关系的面试题。
题目描述
平台：LeetCode
题号：2127
一个公司准备组织一场会议，邀请名单上有 n 位员工。
公司准备了一张圆形的桌子，可以坐下任意数目的员工。
员工编号为 到 。每位员工都有一位喜欢的员工，每位员工当且仅当他被安排在喜欢员工的旁边，他才会参加会议，每位员工喜欢的员工不会是他自己。
给你一个下标从
开始的整数数组 favorite，其中
表示第
位员工喜欢的员工。请你返回参加会议的最多员工数目。
示例 1：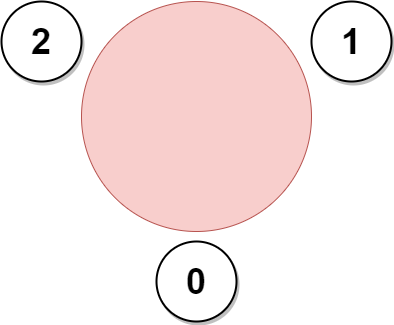 
输入：favorite = [2,2,1,2]
输出：3
解释：
上图展示了公司邀请员工 0，1 和 2 参加会议以及他们在圆桌上的座位。
没办法邀请所有员工参与会议，因为员工 2 没办法同时坐在 0，1 和 3 员工的旁边。
注意，公司也可以邀请员工 1，2 和 3 参加会议。
所以最多参加会议的员工数目为 3 。
示例 2：
输入：favorite = [1,2,0]
输出：3
解释：
每个员工都至少是另一个员工喜欢的员工。所以公司邀请他们所有人参加会议的前提是所有人都参加了会议。
座位安排同图 1 所示：
- 员工 0 坐在员工 2 和 1 之间。
- 员工 1 坐在员工 0 和 2 之间。
- 员工 2 坐在员工 1 和 0 之间。
参与会议的最多员工数目为 3 。
示例 3： 
输入：favorite = [3,0,1,4,1]
输出：4
解释：
上图展示了公司可以邀请员工 0，1，3 和 4 参加会议以及他们在圆桌上的座位。
员工 2 无法参加，因为他喜欢的员工 0 旁边的座位已经被占领了。
所以公司只能不邀请员工 2 。
参加会议的最多员工数目为 4 。
提示：
内向基环森林 + 拓扑排序
根据题意，圆形桌上 左右两边只要有一位是 所喜欢即可。
我们可从 向 添加有向边，从而得到一张包含多个「内向基环树」的图。
内向基环树，是指其满足基环树定义，且内向 bushi。
基环树是指其具有 个点 条边的联通块，而「内向」是指树中任意节点有且只有一条出边，对应的「外向」是指树中任意节点有且只有一条入边。
例如，左图内向，右图外向：
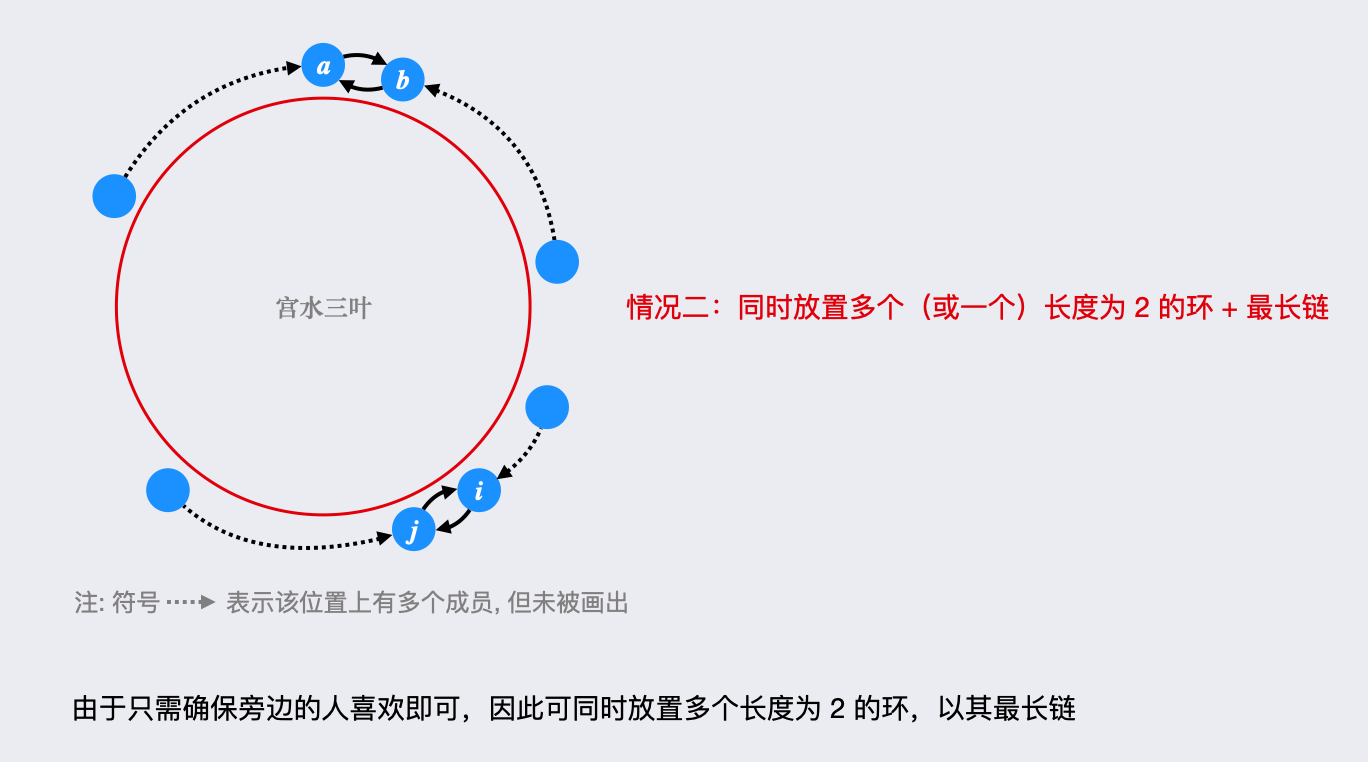
根据题意，「圆桌最多放置一个长度大于 的环（内向环，只有一条出边，即只有一个喜欢的人，安插其他非环成员，会破坏留下参加会议的必要条件），但可放置多个长度为 的环，且多个环可延伸出最长链（利用左右两侧只需有一个喜欢的人即满足）。」
在「取长度大于 的最大环」及「多个长度为 的环及其最长链之和」两者中取最大长度即是答案。
Java 代码：
class Solution {
public int maximumInvitations(int[] favorite) {
int n = favorite.length;
// in 统计每个节点的入度情况, max 统计节最长链
int[] in = new int[n], max = new int[n];
for (int x : favorite) in[x]++;
Deque<Integer> d = new ArrayDeque<>();
for (int i = 0; i < n; i++) {
if (in[i] == 0) d.addLast(i);
}
// 拓扑排序: 求基环外的最长链
while (!d.isEmpty()) {
int cur = d.pollFirst(), ne = favorite[cur];
max[ne] = Math.max(max[ne], max[cur] + 1);
if (--in[ne] == 0) d.addLast(ne);
}
// 圆桌最多放置一个大于 2 的环（ans1 统计最大值）
// 圆桌可放置多个等于 2 的环（ans2 累加该长度）
int ans1 = 0, ans2 = 0;
for (int i = 0; i < n; i++) {
if (in[i] == 0) continue;
int j = favorite[i], cur = 1;
while (j != i) {
// 一个环只需被处理一次, 这里将环中其他节点入度置 0, 下次遍历到这些点就会被跳过
in[j] = 0;
j = favorite[j];
cur++;
}
if (cur == 2) ans2 += 2 + max[i] + max[favorite[i]];
else ans1 = Math.max(ans1, cur);
}
return Math.max(ans1, ans2);
}
}
Python 代码：
class Solution:
def maximumInvitations(self, favorite: List[int]) -> int:
n = len(favorite)
# in_degree 统计每个节点的入度情况, max_length 统计节最长链
in_degree, max_length = [0] * n, [0] * n
for x in favorite:
in_degree[x] += 1
d = deque()
for i in range(n):
if in_degree[i] == 0:
d.append(i)
# 拓扑排序: 求基环外的最长链
while d:
cur = d.popleft()
ne = favorite[cur]
max_length[ne] = max(max_length[ne], max_length[cur] + 1)
in_degree[ne] -= 1
if in_degree[ne] == 0:
d.append(ne)
# 圆桌最多放置一个大于 2 的环（ans1 统计最大值）
# 圆桌可放置多个等于 2 的环（ans2 累加该长度）
ans1, ans2 = 0, 0
for i in range(n):
if in_degree[i] == 0:
continue
j, cur = favorite[i], 1
while j != i:
# 一个环只需被处理一次, 这里将环中其他节点入度置 0, 下次遍历到这些点就会被跳过
in_degree[j] = 0
j = favorite[j]
cur += 1
if cur == 2:
ans2 += 2 + max_length[i] + max_length[favorite[i]]
else:
ans1 = max(ans1, cur)
return max(ans1, ans2)
C++ 代码：
class Solution {
public:
int maximumInvitations(vector<int>& favorite) {
int n = favorite.size();
// in 统计每个节点的入度情况, max_length 统计节最长链
vector<int> in(n, 0);
vector<int> max_length(n, 0);
for (int x : favorite) in[x]++;
deque<int> d;
for (int i = 0; i < n; i++) {
if (in[i] == 0) d.push_back(i);
}
// 拓扑排序: 求基环外的最长链
while (!d.empty()) {
int cur = d.front();
d.pop_front();
int ne = favorite[cur];
max_length[ne] = max(max_length[ne], max_length[cur] + 1);
if (--in[ne] == 0) d.push_back(ne);
}
// 圆桌最多放置一个大于 2 的环（ans1 统计最大值）
// 圆桌可放置多个等于 2 的环（ans2 累加该长度）
int ans1 = 0, ans2 = 0;
for (int i = 0; i < n; i++) {
if (in[i] == 0) continue;
int j = favorite[i], cur = 1;
while (j != i) {
// 一个环只需被处理一次, 这里将环中其他节点入度置 0, 下次遍历到这些点就会被跳过
in[j] = 0;
j = favorite[j];
cur++;
}
if (cur == 2) ans2 += 2 + max_length[i] + max_length[favorite[i]];
else ans1 = max(ans1, cur);
}
return max(ans1, ans2);
}
};
TypeScript 代码：
function maximumInvitations(favorite: number[]): number {
const n = favorite.length;
// in_degree 统计每个节点的入度情况, max_length 统计节最长链
const in_degree = Array(n).fill(0), max_length = Array(n).fill(0);
for (const x of favorite) in_degree[x]++;
const d = [];
for (let i = 0; i < n; i++) {
if (in_degree[i] === 0) d.push(i);
}
// 拓扑排序: 求基环外的最长链
while (d.length > 0) {
const cur = d.shift() as number;
const ne = favorite[cur];
max_length[ne] = Math.max(max_length[ne], max_length[cur] + 1);
if (--in_degree[ne] === 0) d.push(ne);
}
// 圆桌最多放置一个大于 2 的环（ans1 统计最大值）
// 圆桌可放置多个等于 2 的环（ans2 累加该长度）
let ans1 = 0, ans2 = 0;
for (let i = 0; i < n; i++) {
if (in_degree[i] === 0) continue;
let j = favorite[i], cur = 1;
while (j !== i) {
// 一个环只需被处理一次, 这里将环中其他节点入度置 0, 下次遍历到这些点就会被跳过
in_degree[j] = 0;
j = favorite[j];
cur++;
}
if (cur == 2) ans2 += 2 + max_length[i] + max_length[favorite[i]];
else ans1 = Math.max(ans1, cur);
}
return Math.max(ans1, ans2);
};
-
时间复杂度：统计入度的复杂度为 ；拓扑排序求最长链复杂度为 ；计算答案过程中，每个点最多被访问两次（环内节点），复杂度为 。整体复杂度为 -
空间复杂度：
最后
给大伙通知一下 📢 ：
全网最低价 LeetCode 会员目前仍可用！！！
📅 年度会员：有效期加赠两个月！！; 季度会员：有效期加赠两周！！
🧧 年度会员：获 66.66 现金红包！！; 季度会员：获 22.22 现金红包！！
🎁 年度会员：参与当月丰厚专属实物抽奖（中奖率 > 30%)！！
专属链接：leetcode.cn/premium/?promoChannel=acoier
我是宫水三叶，每天都会分享算法知识，并和大家聊聊近期的所见所闻。
欢迎关注，明天见。
更多更全更热门的「笔试/面试」相关资料可访问排版精美的 合集新基地 🎉🎉
扫一扫
635
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
