小米开奖了，这薪资看笑了。。

最新推荐文章于 2024-11-09 12:21:10 发布

宫水三叶的刷题日记

最新推荐文章于 2024-11-09 12:21:10 发布

阅读量1.1k

点赞数 9

文章标签：后端

本文链接：https://blog.csdn.net/weixin_33243821/article/details/143324946

版权

小米

最近小米的「软件开发」岗位开奖了，但遭受到了网友嘲讽，不少同学表示这薪资看笑了 🤣🤣🤣

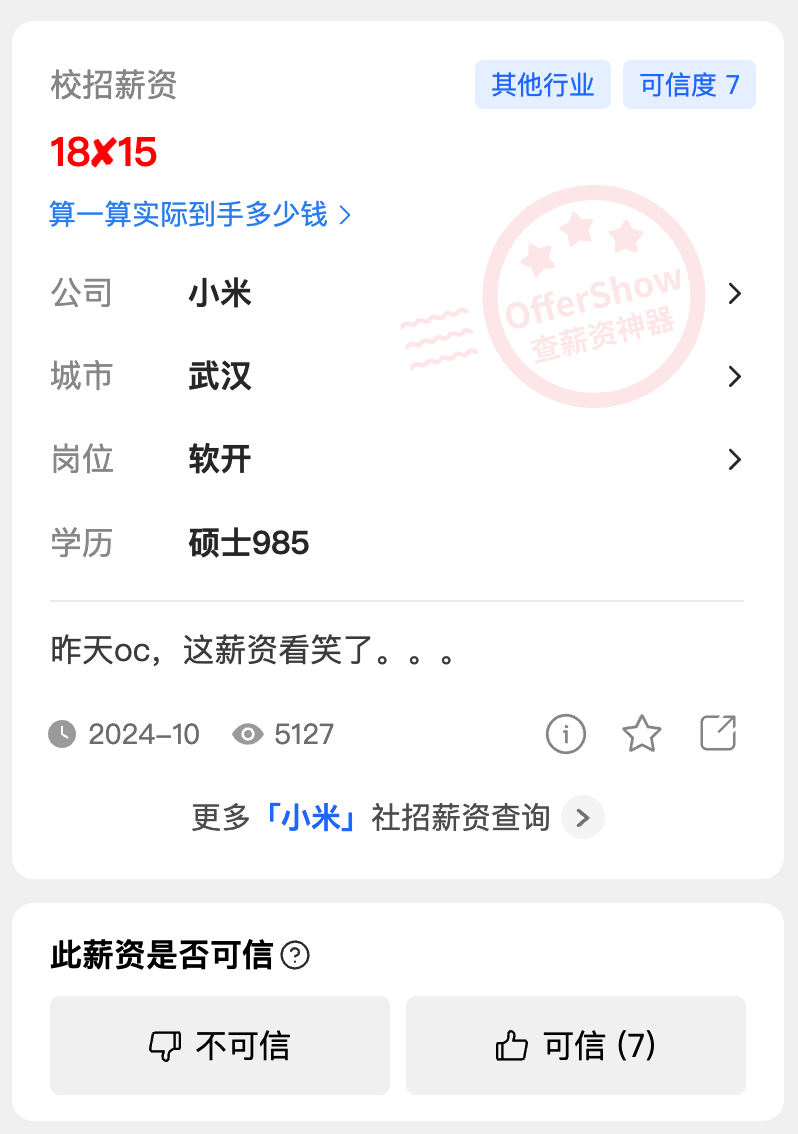
楼主是 985 硕士学历，拿到的是坐标武汉的小米软件开发岗位 offer。

薪资是。

虽然不同候选人的 offer 有所不同，但同为校招的话，通常大差不差。

个人预估，坐标都是武汉的小米软开岗位，月 base 大概在 18k 上下不超过 2k 的范围进行浮动。

这爆料乍一看，15 个月是正常水平，但月 base 只有 18k，似乎不高，但其实如果结合坐标来看，其实还可以。

看一眼武汉其他公司给自家软件开发工程师开的薪资范围就知道了：

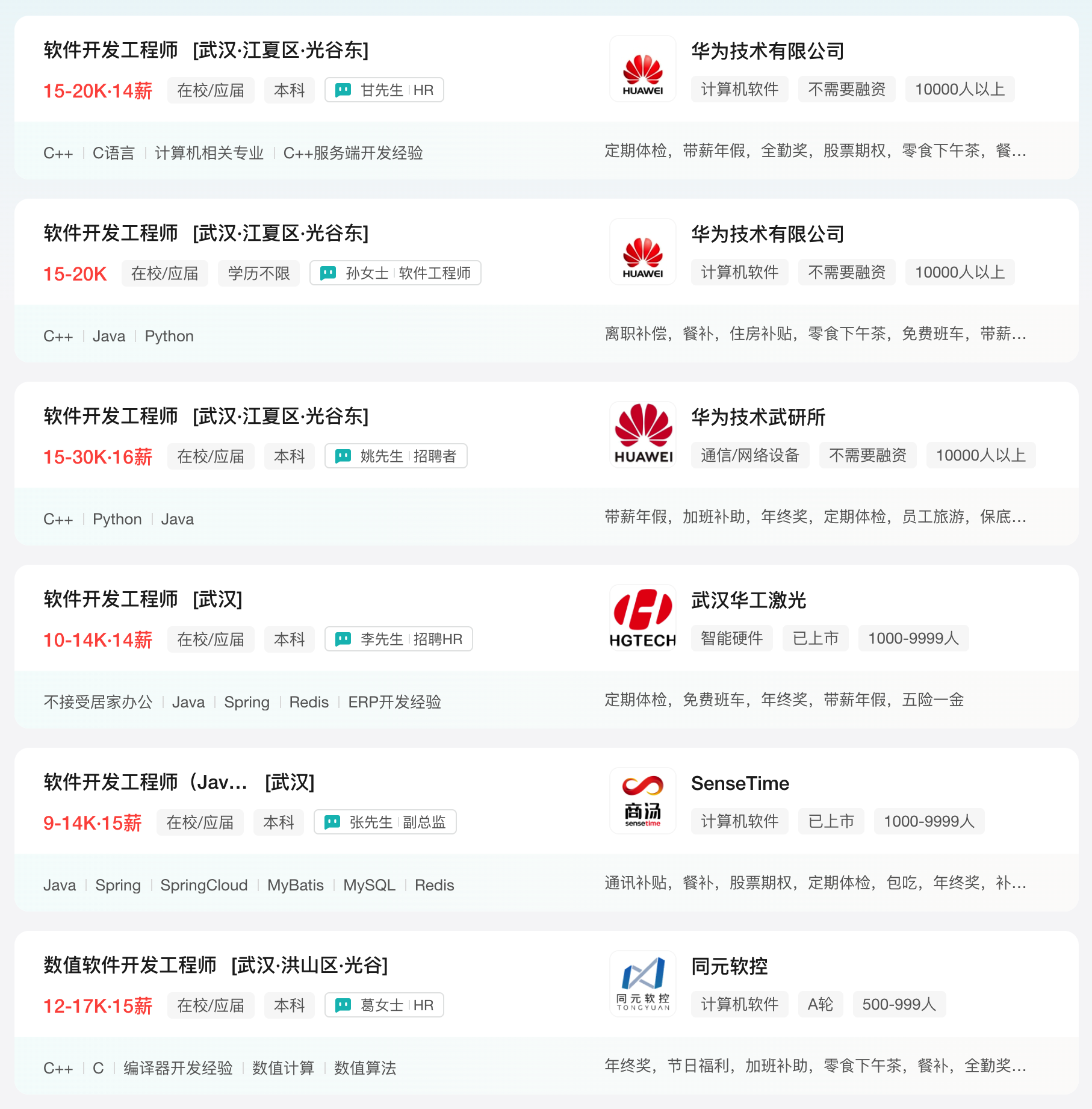
我觉得拿到武汉小米软开 offer 的同学，需要纠结的反而是「这 15 个月到底能不能拿到手」。

对此，你怎么看？小米的开奖价在你预期范围内吗？

...

回归主线。

来一道和「小米校招」相关的算法原题。

题目描述

平台：LeetCode

题号：1482

给你一个整数数组 bloomDay，以及两个整数 m 和 k。

现需要制作 m 束花。制作花束时，需要使用花园中相邻的 k 朵花。

花园中有 n 朵花，第 i 朵花会在 bloomDay[i] 时盛开，恰好可以用于一束花中。

请你返回从花园中摘 m 束花需要等待的最少的天数。如果不能摘到 m 束花则返回 -1。

示例 1：

输入：bloomDay = [1,10,3,10,2], m = 3, k = 1

输出：3

解释：让我们一起观察这三天的花开过程，x 表示花开，而 _ 表示花还未开。
现在需要制作 3 束花，每束只需要 1 朵。
1 天后：[x, _, _, _, _]   // 只能制作 1 束花
2 天后：[x, _, _, _, x]   // 只能制作 2 束花
3 天后：[x, _, x, _, x]   // 可以制作 3 束花，答案为 3

示例 2：

输入：bloomDay = [1,10,3,10,2], m = 3, k = 2

输出：-1

解释：要制作 3 束花，每束需要 2 朵花，也就是一共需要 6 朵花。而花园中只有 5 朵花，无法满足制作要求，返回 -1 。

示例 3：

输入：bloomDay = [7,7,7,7,12,7,7], m = 2, k = 3

输出：12

解释：要制作 2 束花，每束需要 3 朵。
花园在 7 天后和 12 天后的情况如下：
7 天后：[x, x, x, x, _, x, x]
可以用前 3 朵盛开的花制作第一束花。但不能使用后 3 朵盛开的花，因为它们不相邻。
12 天后：[x, x, x, x, x, x, x]
显然，我们可以用不同的方式制作两束花。

示例 4：

输入：bloomDay = [1000000000,1000000000], m = 1, k = 1

输出：1000000000

解释：需要等 1000000000 天才能采到花来制作花束

示例 5：

输入：bloomDay = [1,10,2,9,3,8,4,7,5,6], m = 4, k = 2

输出：9

提示：

二分查找

题目需要求得「所需的最少天数」。

假设「所需的最少天数」为 ans ，那么以 ans 为分割点的数轴具有「二段性」：

天数范围落在无法制作完成
天数范围在可以制作完成

因此可以通过「二分」来找到分割点 ans。

接下来我们需要确定「二分范围」，一个及格的「二分范围」只需要确保答案落在范围即可。

显然范围的左边界为（代表尚未有花绽放），范围的右边界为（最后一朵花的开放时间，代表所有花都开完）。

我们既可以通过遍历数组来取得「精确右边界」，也可以直接根据数据范围 1 <= bloomDay[i] <= 10^9 来确定「粗略右边界」。

由于二分查找本身具有“折半”效率，因此两者不会有太大效率差距，我这里采用「粗略右边界」的方式。

Java 代码：

class Solution {
    int n, m, k;
    boolean[] fl;
    public int minDays(int[] nums, int _m, int _k) {
        n = nums.length;
        m = _m; k = _k;
        if (n < m * k) return -1;
        fl = new boolean[n];
        int l = 0, r = (int)1e9;
        while (l < r) {
            int mid = l + r >> 1;
            if (check(nums, mid)) r = mid;    
            else l = mid + 1;
        }
        return check(nums, r) ? r : -1;
    }
    boolean check(int[] nums, int mid) {
        for (int i = 0; i < n; i++) fl[i] = nums[i] <= mid;
        int cnt = 0;
        for (int i = 0; i < n && cnt < m; ) {
            if (fl[i]) {
                int cur = 1, j = i;
                while (cur < k && j + 1 < n && fl[j + 1]) {
                    j++; cur++;
                }
                if (cur == k) cnt++;
                i = j + 1;
            } else {
                i++;
            }
        }
        return cnt >= m;
    }
}

C++ 代码：

class Solution {
public:
    int n, m, k;
    vector<bool> fl;
    int minDays(vector<int>& nums, int _m, int _k) {
        n = nums.size();
        m = _m; k = _k;
        if (n < m * 1L * k ) return -1;
        fl.resize(n);
        int l = 0, r = 1e9;
        while (l < r) {
            int mid = l + r >> 1;
            if (check(nums, mid)) r = mid;
            else l = mid + 1;
        }
        return check(nums, l) ? l : -1;
    }
    bool check(const vector<int>& nums, int mid) {
        for (int i = 0; i < n; i++) fl[i] = nums[i] <= mid;
        int cnt = 0;
        for (int i = 0; i < n && cnt < m; ) {
            if (fl[i]) {
                int cur = 1, j = i;
                while (cur < k && j + 1 < n && fl[j + 1]) {
                    j++; cur++;
                }
                if (cur == k) cnt++;
                i = j + 1;
            } else {
                i++;
            }
        }
        return cnt >= m;
    }
};

Python 代码：

class Solution:
    def minDays(self, nums: List[int], m: int, k: int) -> int:
        n = len(nums)
        if n < m * k: return -1
        fl = [0] * n
        def check(mid):
            fl = [num <= mid for num in nums]
            cnt, i = 0, 0
            while i < n and cnt < m:
                if fl[i]:
                    cur, j = 1, i
                    while cur < k and j + 1 < n and fl[j + 1]:
                        j, cur = j + 1, cur + 1
                    if cur == k:
                        cnt += 1
                    i = j + 1
                else:
                    i += 1
            return cnt >= m

        l, r = 0, 10**9
        while l < r:
            mid = l + r >> 1
            if check(mid):
                r = mid
            else:
                l = mid + 1
        return check(l) and l or -1

时间复杂度： check 函数的复杂度为。整体复杂度为
空间复杂度：

优化 check 函数

不难发现，上述 check 函数每次都先将所有已开的花预处理出来。复杂度是严格。

其实这个过程也能下放到统计逻辑去做，这样能够让 check 函数的复杂度从严格变为最坏情况，同时省去数组，将空间优化至。

Java 代码：

class Solution {
    int n, m, k;
    public int minDays(int[] nums, int _m, int _k) {
        n = nums.length;
        m = _m; k = _k;
        if (n < m * k) return -1;
        int l = 0, r = (int)1e9;
        while (l < r) {
            int mid = l + r >> 1;
            if (check(nums, mid)) r = mid;    
            else l = mid + 1;
        }
        return check(nums, r) ? r : -1;
    }
    boolean check(int[] nums, int mid) {
        int cnt = 0;
        for (int i = 0; i < n && cnt < m; ) {
            int cur = nums[i] <= mid ? 1 : 0, j = i;
            if (cur > 0) {
                while (cur < k && j + 1 < n && nums[j + 1] <= mid) {
                    j++; cur++;
                }
                if (cur == k) cnt++;
                i = j + 1;
            } else {
                i++;
            }
        }
        return cnt >= m;
    }
}

C++ 代码：

class Solution {
public:
    int n, m, k;
    int minDays(vector<int>& nums, int _m, int _k) {
        n = nums.size();
        m = _m; k = _k;
        if (n < m * 1L * k) return -1;
        int l = 0, r = 1e9;
        while (l < r) {
            int mid = l + r >> 1;
            if (check(nums, mid)) r = mid;
            else l = mid + 1;
        }
        return check(nums, l) ? l : -1;
    }
    bool check(const vector<int>& nums, int mid) {
        int cnt = 0;
        for (int i = 0; i < n && cnt < m; ) {
            int cur = nums[i] <= mid ? 1 : 0, j = i;
            if (cur > 0) {
                while (cur < k && j + 1 < n && nums[j + 1] <= mid) {
                    j++; cur++;
                }
                if (cur == k) cnt++;
                i = j + 1;
            } else {
                i++;
            }
        }
        return cnt >= m;
    }
};

Python 代码：

class Solution:
    def minDays(self, nums: List[int], m: int, k: int) -> int:
        n = len(nums)
        if n < m * k: return -1        
        def check(mid):
            cnt, i = 0, 0
            while i < n and cnt < m:
                cur = 1 if nums[i] <= mid else 0
                j = i
                if cur > 0:
                    while cur < k and j + 1 < n and nums[j + 1] <= mid:
                        j, cur = j + 1, cur + 1
                    if cur == k:
                        cnt += 1
                    i = j + 1
                else:
                    i += 1
            return cnt >= m

        l, r = 0, 10**9
        while l < r:
            mid = l + r >> 1
            if check(mid):
                r = mid
            else:
                l = mid + 1
        return check(l) and l or -1