华为开奖
华为校招也开奖了。
在网上,喜欢和不喜欢这家公司的人都很多,但即便这么多不喜欢的理由,从来没有人吐槽过华为"小气"的。
今年,华为校招在一线城市中仍然有过百万的 Offer(非天才少年计划),而在一些非一线城市当中,部分岗位的待遇也很有竞争力。
目前,坐标「上海」的华为开奖情况爆料最齐全,基本涵盖了各个岗位:
-
上海-通用软件开发:985 硕,22k * 16(年包 35W),职级 14a; -
上海-算法:985 硕,28k * 16(年包 45W),职级 15a; -
上海-数据存储:985 硕,年包 45W~50W,职级 15; -
上海-处理器开发:985 博,年包 70W+,职级 17; -
上海-AIGC 算法:985 博,年包 105W+;
其他城市的开奖情况,只有一些零星的爆料:
-
东莞-结构工程师:985 硕,24k * (14~16),在东莞算是 SP/SSP; -
北京-鸿蒙开发:985 硕,22k * 15; -
杭州-鸿蒙开发:985 硕,25k * (14~16); -
深圳-算法:985 硕,年包 40W; -
武汉-结构工程师:211 硕,22k * (12~15);
对此,你怎么看?如果手上有多个待遇相近的 Offer,你会优先选择华为吗?欢迎评论区交流。
...
回归主题。
来一道和「华为」相关的算法题。
题目描述
平台:LeetCode
题号:179
给定一组非负整数 nums,重新排列每个数的顺序(每个数不可拆分)使之组成一个最大的整数。
注意:输出结果可能非常大,所以你需要返回一个字符串而不是整数。
示例 1:
输入:nums = [10,2]
输出:"210"
示例 2:
输入:nums = [3,30,34,5,9]
输出:"9534330"
示例 3:
输入:nums = [1]
输出:"1"
示例 4:
输入:nums = [10]
输出:"10"
提示:
贪心
对于 中的任意两个值 和 ,我们无法直接从常规角度上确定其大小/先后关系。
但我们可以根据「结果」来决定 和 的排序关系:
如果拼接结果 要比 好,那么我们会认为 应该放在 前面。
另外,注意我们需要处理前导零(最多保留一位)。
Java 代码:
class Solution {
public String largestNumber(int[] nums) {
int n = nums.length;
String[] ss = new String[n];
for (int i = 0; i < n; i++) ss[i] = "" + nums[i];
Arrays.sort(ss, (a, b) -> {
String sa = a + b, sb = b + a ;
return sb.compareTo(sa);
});
StringBuilder sb = new StringBuilder();
for (String s : ss) sb.append(s);
int len = sb.length();
int k = 0;
while (k < len - 1 && sb.charAt(k) == '0') k++;
return sb.substring(k);
}
}
C++ 代码:
class Solution {
public:
string largestNumber(vector<int>& nums) {
int n = nums.size();
vector<string> ss(n);
for (int i = 0; i < n; i++) ss[i] = to_string(nums[i]);
sort(ss.begin(), ss.end(), [](const string& a, const string& b) {
return a + b > b + a;
});
string result;
for (const string& s : ss) result += s;
int len = result.length(), k = 0;
while (k < len - 1 && result[k] == '0') k++;
return result.substr(k);
}
};
Python 代码:
class Solution:
def largestNumber(self, nums: List[int]) -> str:
nums = list(map(str, nums))
nums.sort(key=lambda x: x * 10, reverse=True)
result = ''.join(nums)
k = 0
while k < len(result) - 1 and result[k] == '0':
k += 1
return result[k:]
TypeScript 代码:
function largestNumber(nums: number[]): string {
const ss = nums.map(num => num.toString());
ss.sort((a, b) => (b + a).localeCompare(a + b));
let result = '';
for (const s of ss) result += s;
let k = 0;
while (k < result.length - 1 && result[k] === '0') k++;
return result.substring(k);
};
-
时间复杂度:由于是对 进行排序,当排序对象不是 中的基本数据类型时,不会使用快排(考虑排序稳定性问题)。 Java中的Arrays.sort()的底层实现会「元素数量/元素是否大致有序」决定是使用插入排序还是归并排序。这里直接假定使用的是「插入排序」。复杂度为 -
空间复杂度:
证明
上述解法,我们需要证明两个内容:
-
该贪心策略能取到全局最优解。 -
这样的「排序比较逻辑」应用在集合 上具有 「全序关系」。
1. 该贪心策略能取到全局最优解
令我们经过这样的贪心操作得到的贪心解为 ,真实最优解为 。
由于真实最优解为全局最大值,而我们的贪心解至少是一个合法解(一个数),因此天然有 。
「接下来我们只需要证明 ,即可得 (贪心解即为最优解)。」
我们使用「反证法」来证明 成立:
假设 不成立,即有 。
和 都是由同样一批数字凑成的,如果有 。
这意味着我们可以将 中的某些低位数字和高位数字互换,使得 更大(调整为 ),这与我们根据「结果」进行排序的逻辑冲突。
因此 必然不成立,得证 成立,结合 可得贪心解为最优。
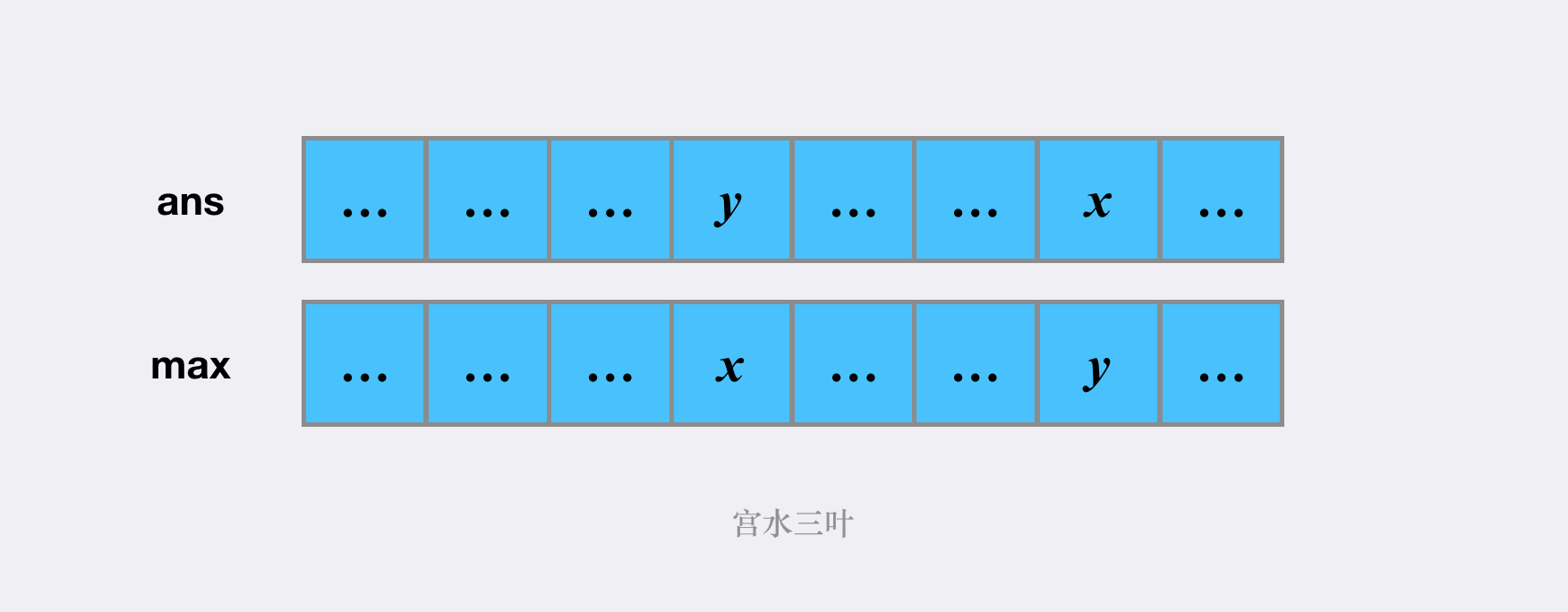
举个🌰,如果有 ,那么意味着在 中至少有一对数字互换可以使得 变大,
那么在排序逻辑中 所在的整体(可能不只有 一个数)应该被排在 所在的整体(可能不只有 一个数)前面。
2. 全序关系
我们使用符号 来代指我们的「排序」逻辑:
-
如果 必须排在 的前面,我们记作 ; -
如果 必须排在 的后面,我们记作 ; -
如果 既可以排在 的前面,也可以排在 的后面,我们记作 ;
2.1 完全性
具有完全性是指从集合 中任意取出两个元素 和 ,必然满足 、 和 三者之一。
这点其实不需要额外证明,因为由 和 拼接的字符串 和 所在「字典序大小关系中」要么完全相等,要么具有明确的字典序大小关系,导致 必须排在前面或者后面。
2.2 反对称性
具有反对称性是指由 和 能够推导出 。
说明字符串 的字典序大小数值要比字符串 字典序大小数值大。
说明字符串 的字典序大小数值要比字符串 字典序大小数值小。
这样,基于「字典序本身满足全序关系」和「数学上的 和 可推导出 」。
得证 和 能够推导出 。
2.3 传递性
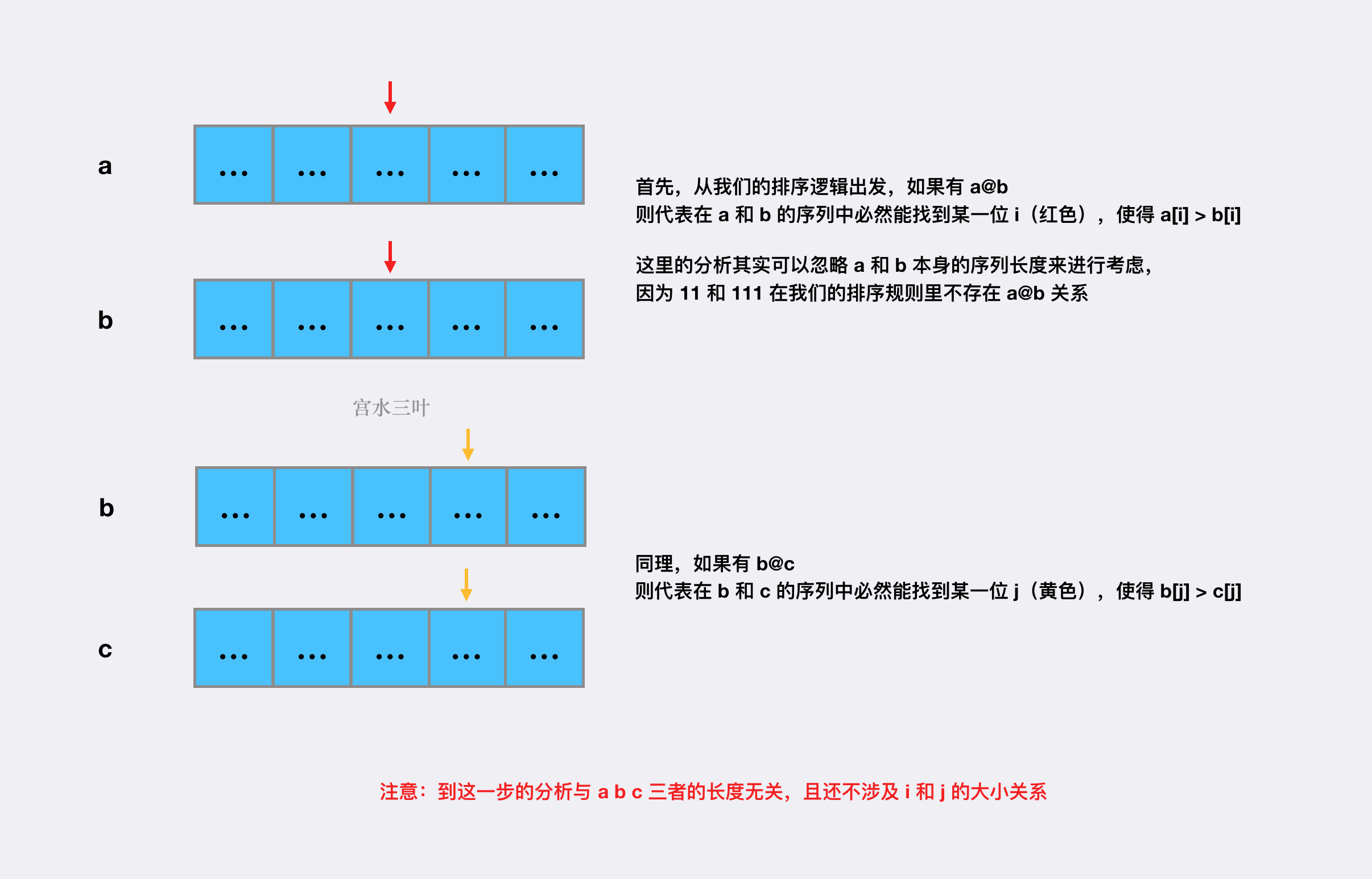
具有传递性是指由 和 能够推导出 。
这里的「传递性」其实也可以使用与 官方题解 类似的手法来证明。
我们可以利用「两个等长的拼接字符串,字典序大小关系与数值大小关系一致」这一性质来证明,因为字符串 和 必然是等长的。
接下来,让我们从「自定义排序逻辑」出发,换个思路来证明 :
然后我们只需要证明在不同的 关系之间(共三种情况), 恒成立即可:
-
当 的时候:
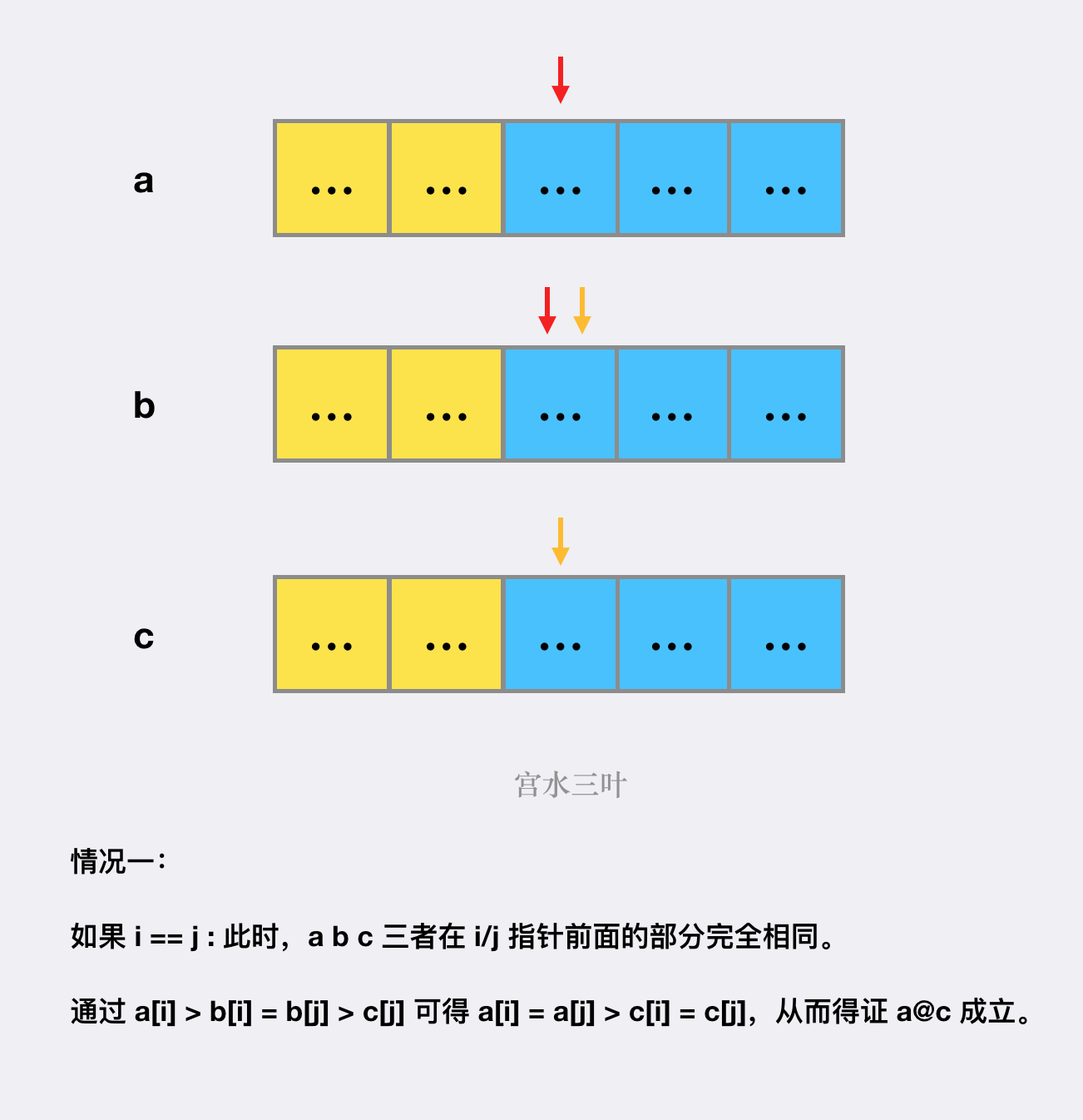
-
当 的时候:
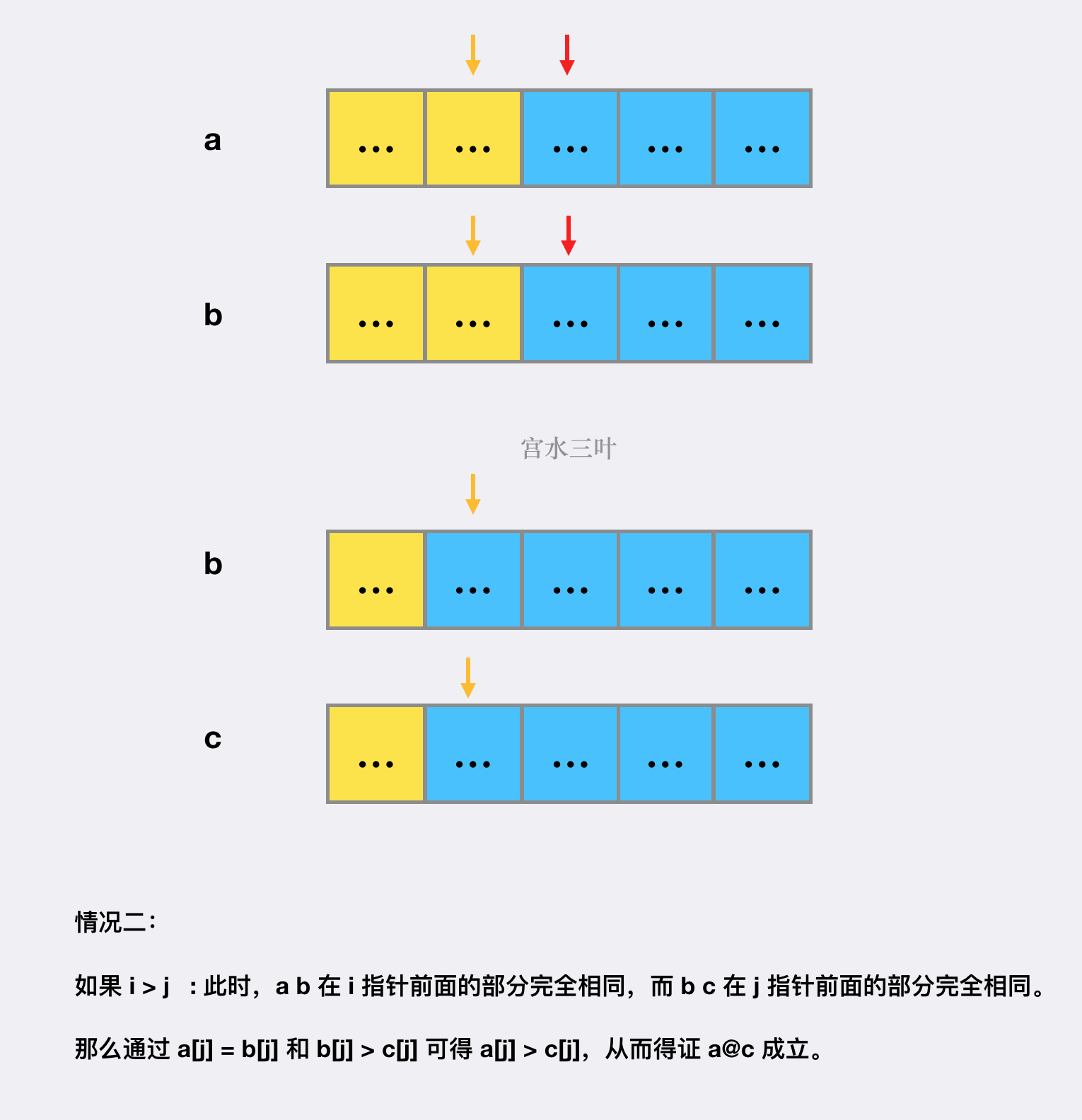
-
当 的时候:
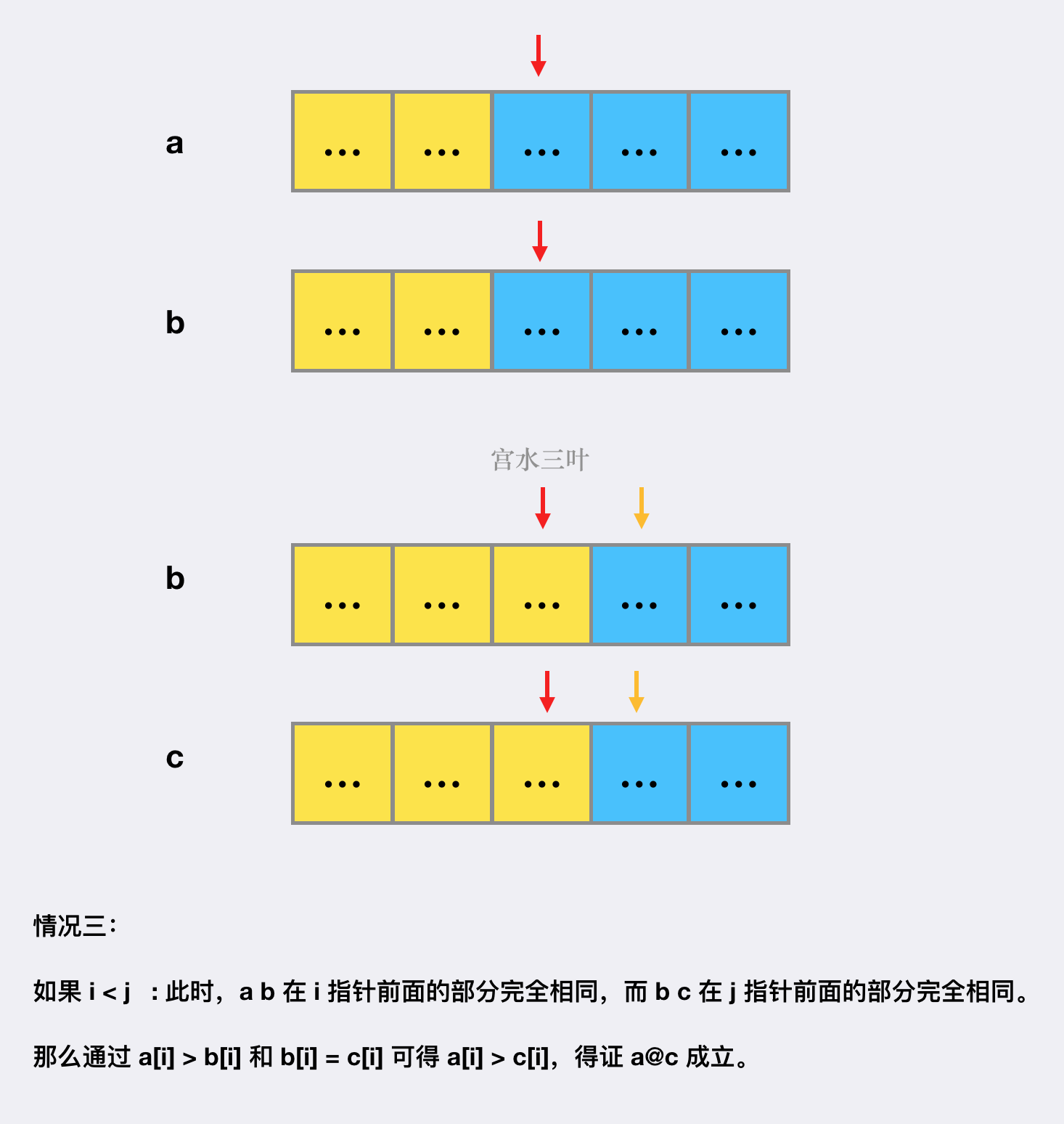
综上,我们证明了无论在何种情况下,只要有 和 的话,那么 恒成立。
我们之所以能这样证明「传递性」,本质是利用了自定义排序逻辑中「对于确定任意元素 和 之间的排序关系只依赖于 和 的第一个不同元素之间的大小关系」这一性质。
找 i 的越界问题
考虑
(1) a = 304 b = 30 (2) a = 301 b = 30
两种情况。
显然,(1)下我们会得到 ,而(2)下我们会得到
但是,在这种情况下 实际上位于 界外,那我们还能不能找 呢? 是多少呢?
实际上是可以的,我们在比较
和
的时候,实际上是在比较
和
两个字符串,所以实际上我们是在用
,
,
... 去填补
本体结束后的空缺。换而言之(1)和(2)里的 b 实际上被填补为 303 (填进来
)
再比如
(3)a = 3131248 b = 3131 ,比较的时候实际上是用
开头的 4 位去填补上
的空缺,所以
实际上相当于 31313131
最后
巨划算的 LeetCode 会员优惠通道目前仍可用 ~
使用福利优惠通道 leetcode.cn/premium/?promoChannel=acoier,年度会员 有效期额外增加两个月,季度会员 有效期额外增加两周,更有超大额专属 🧧 和实物 🎁 福利每月发放。
我是宫水三叶,每天都会分享算法知识,并和大家聊聊近期的所见所闻。
欢迎关注,明天见。
更多更全更热门的「笔试/面试」相关资料可访问排版精美的 合集新基地 🎉🎉
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








