已知斜边和角度求邻边_中考数学压轴题分析：圆中构造相似求线段长

本文内容以圆为背景求线段长度。与2018年广东省的中考数学压轴题类似。大家可以对比一下。

【中考真题】

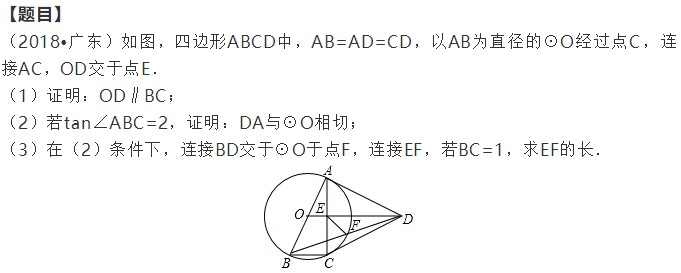
(2020·自贡)如图，⊙O是△ABC的外接圆，AB为直径，点P为⊙O外一点，且PA＝PCAB，连接PO交AC于点D，延长PO交⊙O于点F．
(1)证明：；
(2)若tan∠ABC＝2，证明：PA是⊙O的切线；
(3)在(2)条件下，连接PB交⊙O于点E，连接DE，若BC＝2，求DE的长．

【分析】

题(1)中证明两条弧相等，说明它们被直径平分，那么可以考虑垂径定理的推论进行证明也就是得到OD⊥AC即可。那怎么证明它们垂直呢？条件已知PA=PC，所以可以考虑连接OC得到OC=OA，那么就可以根据垂直平分线的判定进行证明。

题(2)证明PA是切线，只需证明∠BAP=90°即可。已知tan∠ABC的值，那么可以设最短的BC=x，就可以表示出AB、AP、AD的值，然后得到△DAP∽△CBA，即可得到∠DAP=∠ABC，再得到∠BAP=90°即可。

题(3)需要求DE的长度，我们考虑的是利用勾股、相似等知识进行求解。但是没有相关的直角或相似。所以需要构造辅助线。由于AB是直径，可以连接AE，那么就可以得到AE是△ABP斜边上的高。由于BC长度已知，那么△ABP中的所有边长都可以表示出来，也知道BE：EP=1：2，那么就有很多方法可以求了。

连接BF，可以证明一个A字形的相似，求出BF的长度即可。

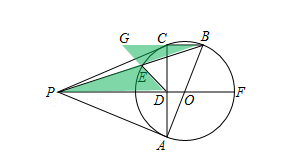
如上图，当然也可以构造蝴蝶型相似，求出BG、DG的长度即可得到DE的长度。

本题的图形与2018年的广东省中考数学压轴题类似。

一题十二解

【答案】(1)证明：连接OC．
∵PC＝PA，OC＝OA，
∴OP垂直平分线段AC，
∴．

(2)证明：设BC＝a，
∵AB是直径，
∴∠ACB＝90°，
∵tan∠ABC2，
∴AC＝2a，AB3a，
∴OC＝OA＝OB，CD＝ADa，
∵PA＝PCAB，
∴PA＝PC＝3a，
∵∠PDC＝90°，
∴PD4a，
∵DC＝DA，AO＝OB，
∴ODBCa，
∴AD2＝PD•OD，
∴，
∵∠ADP＝∠ADO＝90°，
∴△ADP∽△ODA，
∴∠PAD＝∠DOA，
∵∠DOA+∠DAO＝90°，
∴∠PAD+∠DAO＝90°，
∴∠PAO＝90°，
∴OA⊥PA，
∴PA是⊙O的切线．

(3)解：如图，过点E作EJ⊥PF于J，BK⊥PF于K．
∵BC＝2，
由(1)可知，PA＝6，AB＝6，
∵∠PAB＝90°，
∴PB6，
∵PA2＝PE•PB，
∴PE4，
∵∠CDK＝∠BKD＝∠BCD＝90°，
∴四边形CDKB是矩形，
∴CD＝BK＝2，BC＝DK＝2，
∵PD＝8，
∴PK＝10，
∵EJ∥BK，
∴，
∴，
∴EJ，PJ，
∴DJ＝PD﹣PJ＝8，
∴DE．

京东商城

https://item.jd.com/12783241.html

当当网

http://product.dangdang.com/29176976.html

天猫商城

https://detail.tmall.com/item.htm?spm=a211lz.success.0.0.2ca42b90utqwAG&id=636222759859

点击阅读原文，也可以进入哦！