简介:模糊控制算法,基于模糊逻辑的控制策略,在不确定性和非线性系统中有突出表现。本项目展示如何用纯MATLAB代码实现一个模糊控制系统,不依赖MATLAB系统函数,深入理解模糊逻辑和MATLAB编程。项目详细说明了模糊控制的基本思想,包括模糊化、规则推理和去模糊化三个主要步骤,并提供了关于系统设计的说明、实验数据以及功能块说明,有助于理解代码结构和工作流程。MATLAB中使用M文件编写了主控制程序和相关函数,为学习和应用模糊控制提供实践经验。 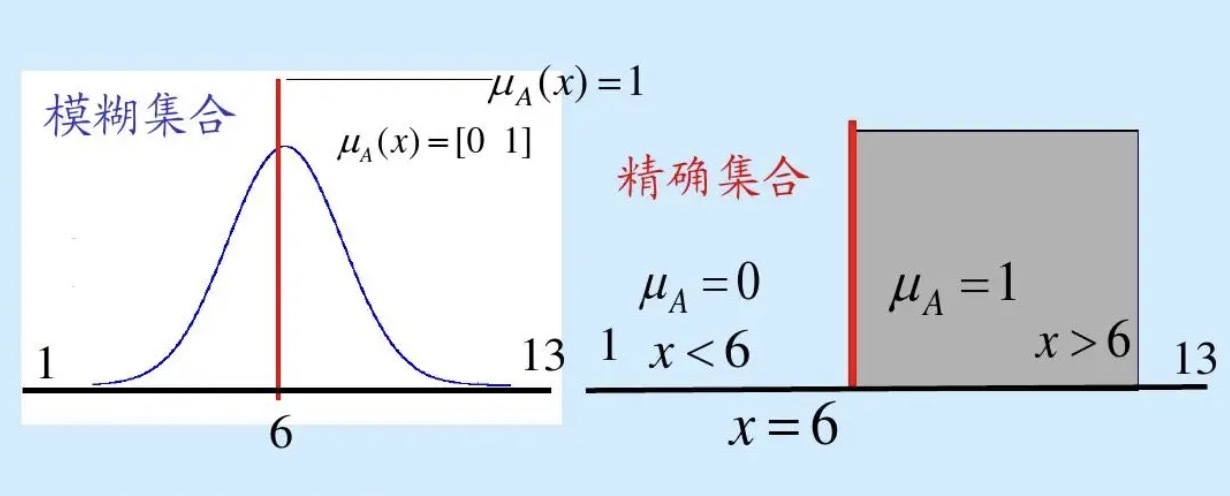
1. 模糊控制算法概念与应用
模糊控制算法的基本原理
模糊控制算法是一种基于模糊逻辑的控制方法,主要用来处理含糊不清或不确定的条件。模糊逻辑系统的核心在于将传统逻辑中的“非此即彼”的判断方式转变为“亦此亦彼”的隶属度函数,从而可以处理如语言变量这样的非数值化问题。它通过定义输入输出变量的模糊集合和模糊规则来模仿人的决策过程,这使得模糊控制器特别适合于那些难以用精确数学模型描述的复杂系统。
模糊控制算法在实际中的应用领域和案例分析
模糊控制在很多领域都有其成功的应用案例,包括家用电器(如洗衣机、空调)、汽车(如防滑制动系统)、工业过程控制以及在人工智能领域中的应用(比如机器人导航)。以洗衣机为例,模糊控制器能够根据衣服的重量、脏污程度等因素调整洗涤时间、水温等参数,从而达到较好的洗净效果和节能目标。这些应用显示了模糊控制算法在实际问题解决中的巨大潜力。
2. MATLAB实现模糊控制的优势
2.1 MATLAB软件在模糊控制算法中的优势
模糊控制算法作为一种智能控制方法,其设计和实现过程往往需要强大的数学建模和仿真分析能力。MATLAB(Matrix Laboratory的缩写)作为一种高性能的数值计算和可视化软件,为模糊控制算法的实现提供了诸多便利。
MATLAB具有以下几点优势:
-
强大的数学计算能力: MATLAB提供了丰富且高效的数学函数库,涵盖了线性代数、矩阵运算、数值分析等各个领域。这对于构建和解析模糊控制器中的数学模型至关重要。
-
直观的编程环境: MATLAB的编程语言简洁直观,易于学习和使用,特别适合进行算法原型设计和快速开发。
-
丰富的工具箱支持: MATLAB拥有专门针对模糊逻辑的Fuzzy Logic Toolbox,该工具箱提供了模糊系统设计所需的各种函数和模块,极大地简化了模糊逻辑控制器的创建和测试过程。
-
强大的仿真环境: Simulink是MATLAB的一个附加产品,它提供了一个图形化的环境用于构建复杂的动态系统模型。用户可以通过拖放的方式快速搭建模糊控制系统,并进行实时仿真和分析。
-
便捷的数据可视化: MATLAB的数据可视化功能强大,可以轻松创建二维和三维图形,对于分析模糊控制系统的性能和结果非常有帮助。
2.2 MATLAB在模糊控制中的实际应用案例分析
让我们以一个温度控制系统的模糊控制为例,探讨MATLAB在实现模糊控制中的具体应用。
2.2.1 系统背景
假定我们有一个温室环境控制系统,需要通过模糊控制算法维持环境温度在一个恒定范围内。温度的设定范围为22°C至25°C,需要控制器对加热器和冷却器进行动态调节。
2.2.2 模糊控制器设计
利用MATLAB的Fuzzy Logic Toolbox,我们可以轻松设计出一个模糊控制器。设计过程大致可以分为以下几个步骤:
-
定义模糊变量: 包括温度误差(Error)和温度误差变化率(Change Rate)。每个变量都需要定义对应的模糊集和隶属函数。
-
定义模糊规则: 根据控制系统的需求,确定模糊规则。比如,如果温度过高且升温过快,则需要大力降温。
-
控制器配置: 通过Fuzzy Logic Designer工具箱,可以直观地设置各个模糊变量的隶属函数,以及构建模糊规则库。
-
仿真实验: 使用MATLAB进行仿真实验,验证模糊控制系统的性能。通过输入不同的温度设定值,观察系统对加热器和冷却器的控制策略和最终效果。
2.3 MATLAB代码实现
下面是使用MATLAB代码实现模糊控制器的基本框架:
% 模糊逻辑控制器的创建和初始化
fis = mamfis('Name', 'GreenhouseControl');
% 添加模糊变量和隶属函数
fis = addInput(fis, [-10 10], 'Name', 'Error');
fis = addMF(fis, 'Error', 'gaussmf', 'sigma', 3);
fis = addInput(fis, [-5 5], 'Name', 'Change Rate');
fis = addMF(fis, 'Change Rate', 'trimf', [-5 -2.5 0]);
fis = addOutput(fis, [-10 10], 'Name', 'Control Action');
fis = addMF(fis, 'Control Action', 'trimf', [-10 -5 0]);
% 添加模糊规则
ruleList = [
1 1 1 1 1;
2 1 2 1 1;
% ... 更多规则
];
fis = addRule(fis, ruleList);
% 仿真
data = simulate(fis, [模拟数据]);
在上述代码中,我们创建了一个名为 GreenhouseControl 的模糊逻辑控制器,定义了输入变量 Error 和 Change Rate 以及输出变量 Control Action 。我们使用了高斯函数和三角形函数作为隶属函数,并添加了一系列模糊规则。最后,通过 simulate 函数对控制器进行仿真测试。
2.4 总结
MATLAB在实现模糊控制算法方面提供了强大的支持,不仅在数学计算和编程上提供了极大的便利,而且在模糊控制器的设计、仿真以及优化方面均能提供专业和高效的解决方案。通过具体案例和代码实现,我们看到MATLAB可以帮助工程师快速完成模糊控制器的搭建和验证,显著提升了开发效率和系统性能。在下一章中,我们将进一步深入探讨模糊化的实现方法。
3. 模糊化的实现方法
在本章中,我们将深入了解模糊化在模糊控制系统中的核心作用。模糊化是将精确输入数据转换为模糊集的过程,这是模糊控制算法实现其控制决策能力的关键步骤。本章将探讨模糊化的原理,以及如何在MATLAB环境中实现这一过程。
模糊化的基本原理和步骤
模糊化的定义与重要性
模糊化是指将输入数据从精确值转换为模糊值的过程,即将具体的数值映射到模糊集(如“低”、“中”、“高”)的过程。这种转换允许控制系统以一种近似人类思考的方式来处理不确定性,并做出控制决策。在复杂的系统中,如温度控制、自动驾驶等,模糊化提供了一种简便的方式来处理非线性、不确定性的输入。
模糊化的步骤
- 定义输入变量的模糊集 :首先需要定义每个输入变量的可能模糊集(如“冷”、“温暖”、“热”),每个模糊集对应一个隶属度函数,用于确定任意输入值属于该模糊集的程度。
- 确定隶属度函数 :隶属度函数可以是三角形、梯形、高斯型等多种形状,这些函数定义了输入变量的模糊集的边界以及隶属度如何随输入值变化。
- 应用隶属度函数到输入数据 :将输入数据应用到隶属度函数上,得到每个数据点对于每个模糊集的隶属度值。
- 模糊规则的建立 :根据专家知识或数据,建立一组规则来定义如何根据输入变量的模糊值进行决策。
模糊化的实例分析
为了具体理解模糊化过程,考虑一个简单的例子:家庭温度控制器。我们定义输入变量为室内温度,其模糊集包括“低”、“中”、“高”。隶属度函数可以简单地定义如下:
- 低(L) :温度低于设定温度的5度或以上。
- 中(M) :温度在设定温度的±5度范围内。
- 高(H) :温度高于设定温度的5度或以上。
模糊化过程将室内温度值映射到这三个模糊集,并计算出对应每个模糊集的隶属度。
使用MATLAB实现模糊化的方法和步骤
MATLAB工具介绍
MATLAB提供了一个名为Fuzzy Logic Toolbox的工具箱,专门用于设计和模拟模糊逻辑系统。该工具箱包括了模糊化、规则建立、模糊推理、去模糊化等步骤的工具。
使用MATLAB进行模糊化的步骤
- 打开Fuzzy Logic Designer :在MATLAB命令窗口中输入
fuzzyDesigner或在MATLAB的APPs中找到Fuzzy Logic Designer并打开。 - 创建新的模糊逻辑系统 :选择File -> New -> Fuzzy Inference System,打开一个新的窗口用于定义模糊系统。
- 定义输入和输出变量 :点击Input/Output编辑框,定义输入和输出变量及其模糊集。为每个变量添加模糊集(如L, M, H)并设置隶属度函数的参数。
- 设置隶属度函数 :点击每个输入变量旁边的Membership Function编辑框,设置隶属度函数的形状和参数。MATLAB提供了多种预设的隶属度函数类型,可以直观地调整其参数。
- 添加规则 :在Rule Editor中添加模糊控制规则。规则的格式为:“如果(输入1是X1)且(输入2是X2)... 那么(输出是Y)”。
- 进行模糊化操作 :一旦输入变量、输出变量、隶属度函数和规则都定义好,就可以通过输入具体的输入值来观察模糊化的效果。选择Simulate -> Enter input values,输入具体数值后,点击Simulate,观察输出的模糊集隶属度。
示例代码和解释
以下是MATLAB中实现模糊化的代码示例:
% 创建一个新的模糊推理系统
fis = newfis('HomeTempControl');
% 添加输入变量和输出变量
fis = addvar(fis, 'input', 'ActualTemp', [15 35]);
fis = addmf(fis, 'input', 1, 'Low', 'trapmf', [15 15 20 25]);
fis = addmf(fis, 'input', 1, 'Medium', 'trimf', [22 25 28]);
fis = addmf(fis, 'input', 1, 'High', 'trapmf', [25 35 35 35]);
fis = addvar(fis, 'output', 'HeaterControl', [0 100]);
fis = addmf(fis, 'output', 1, 'Low', 'trimf', [0 0 50]);
fis = addmf(fis, 'output', 1, 'High', 'trimf', [50 100 100]);
% 添加模糊规则
ruleList = [1 1 1 1 1 1 1];
ruleList(1:3) = [1 1 1 1 1 1 1; 2 1 1 2 1 1 1; 3 1 1 3 1 1 1];
fis = addrule(fis, ruleList);
% 模拟模糊化过程
inputValue = 24; % 实际温度输入值
outputValue = evalfis(fis, inputValue);
disp(['HeaterControl output for input ' num2str(inputValue) ' is ' num2str(outputValue)]);
在上述代码中,我们首先创建了一个名为 HomeTempControl 的模糊推理系统,接着定义了输入变量 ActualTemp 及其模糊集,以及输出变量 HeaterControl 及其模糊集。然后,我们添加了一组简单的模糊规则,最后通过 evalfis 函数对输入值 24 进行模拟,得到输出值。
通过上述步骤,我们不仅实现了模糊化的过程,还验证了其在MATLAB中的具体操作。这为在实际应用中设计和调试模糊控制系统提供了便利。
接下来的章节将继续深入探讨模糊规则库的构建,以及如何在MATLAB中构建和优化模糊规则库,使模糊控制系统更加精确和高效。
4. 模糊规则库的构建
模糊规则库的概念和重要性
模糊规则库是模糊控制器的核心部分,它包含了将输入变量映射到输出变量的一系列规则。这些规则是基于专家知识或者操作经验形成的,用于描述不同输入条件下应该采取的控制行为。构建一个合理的模糊规则库对于实现有效的模糊控制至关重要,因为它直接决定了控制系统的性能和决策质量。
模糊规则通常以“IF-THEN”的逻辑语句形式出现,例如:“IF 温度是冷的 AND 压力是低的 THEN 火力是强的”。每个规则都定义了一个模糊关系,这些关系通过模糊逻辑操作被组合起来,形成控制决策。
模糊规则库的重要性
- 决策的准确性 :清晰定义的规则库能够使控制器更好地理解和响应系统状态的变化,从而做出更为准确的决策。
- 系统响应的稳定性 :合理的规则库有助于避免控制系统在操作过程中产生剧烈波动,保证系统的稳定运行。
- 适应性 :良好的规则库设计能够在系统参数发生变化时提供更好的适应性,保证控制器的鲁棒性。
- 易扩展性 :规则库的构建方法应便于增加新的规则,以适应复杂系统的变化或者新的控制要求。
如何在MATLAB中构建和优化模糊规则库
第一步:定义模糊变量和隶属函数
在MATLAB中,使用Fuzzy Logic Toolbox可以方便地定义模糊变量及其隶属函数。隶属函数定义了变量在特定模糊集中的隶属度,是模糊逻辑的基础。
% 定义温度变量及其隶属函数
temp = [0 15 30 45]; % 温度范围
lowTemp = [0 0 1 1];
mediumTemp = [1 1 0 0];
highTemp = [0 0 0 0];
% 定义压力变量及其隶属函数
pressure = [0 5 10 15]; % 压力范围
lowPressure = [0 0 1 1];
mediumPressure = [1 1 0 0];
highPressure = [0 0 0 0];
% 定义火力变量及其隶属函数
firePower = [0 25 50 75]; % 火力范围
weakFire = [1 1 0 0];
mediumFire = [0 1 1 0];
strongFire = [0 0 1 1];
第二步:创建模糊规则
在MATLAB中,可以使用 addRule 函数添加规则。规则的创建需要基于定义好的模糊变量和隶属函数。
% 创建模糊规则
ruleList = [
"If (temp is lowTemp) and (pressure is lowPressure), then (firePower is strongFire)"
"If (temp is mediumTemp) and (pressure is mediumPressure), then (firePower is mediumFire)"
"If (temp is highTemp) and (pressure is highPressure), then (firePower is weakFire)"
];
% 添加规则到模糊推理系统
for i = 1:length(ruleList)
addRule(fis, ruleList(i));
end
第三步:优化模糊规则库
优化模糊规则库通常涉及调整规则权重、减少规则冗余或者引入新的规则以提升系统性能。MATLAB提供了工具帮助用户通过图形界面进行规则调整。
% 调整规则权重
ruleList{1}.Weight = 0.7;
% 运行模糊推理系统进行测试
inputTemp = 25;
inputPressure = 10;
outputFirePower = evalfis([inputTemp, inputPressure], fis);
% 分析结果并调整规则库
if outputFirePower < 45
% 如果火力输出不满足需求,考虑增加更强火力的规则
addRule(fis, "If (temp is mediumTemp) and (pressure is highPressure), then (firePower is strongFire)");
end
第四步:测试和验证模糊规则库
在构建完模糊规则库后,需要进行一系列的测试,以确保规则库能够准确反映控制需求,并且在各种条件下都能产生稳定的控制效果。
% 使用测试数据对模糊控制器进行验证
testData = [10, 5; 30, 15; 40, 10];
outputData = zeros(size(testData));
for i = 1:size(testData, 1)
outputData(i) = evalfis([testData(i,1), testData(i,2)], fis);
end
% 分析输出结果,验证控制器性能
第五步:使用MATLAB工具箱进行可视化分析
MATLAB的Fuzzy Logic Toolbox提供了一套完整的工具箱,可以用来对模糊规则库进行可视化分析。这些工具可以帮助用户更好地理解规则库的动态特性,并且进行相应的调整。
% 生成模糊规则矩阵进行分析
ruleMatrix = evalfis([temp, pressure], fis);
% 可视化模糊规则矩阵
figure;
imagesc(ruleMatrix);
colormap(jet(256));
colorbar;
title('Fuzzy Rule Matrix Visualization');
xlabel('Temperature');
ylabel('Pressure');
通过上述五个步骤,我们不仅在MATLAB中成功构建了一个基本的模糊规则库,而且介绍了如何对规则库进行优化和验证。在实践中,这需要不断地迭代和细化,通过实验和测试来不断改进,直到达到期望的控制效果。
5. 去模糊化的转换方法
去模糊化是模糊控制的最后一个关键步骤,在这个过程中,模糊输出需要被转化为可以用于控制系统具体操作的精确数值。去模糊化的目的是为了使得模糊控制器的决策可以被真实世界所接受,这样的输出可以被控制器用来实际操作机械设备或者进行决策。
去模糊化的基本原理和步骤
去模糊化的原理是将模糊逻辑系统输出的模糊集合转换成一个单一的、明确的数值。这个过程通常基于几个不同方法实现,其中最常用的包括:
- 最大隶属度法(Max Membership)
- 中心平均解模糊化法(Centroid Method)
- 加权平均法(Weighted Average Method)
- 最大值法(Mean of Maximum)
每种方法都有其适用性和限制,选择去模糊化方法时需要根据实际应用场景和控制要求进行考量。
实现步骤
一般来说,去模糊化的实现步骤如下:
- 确定输出模糊集 :这是根据模糊规则和输入模糊集进行模糊推理得出的。
- 选择去模糊化方法 :根据控制系统要求和输出的特性来决定。
- 计算去模糊化值 :应用所选择的方法计算出单一数值。
- 应用去模糊化值 :将得到的明确值应用于控制过程中。
代码实现
以下是一个简单的MATLAB代码示例,演示了如何使用中心平均解模糊化法进行去模糊化处理:
% 假设已经有了一个模糊化的输出集合
% 输出集合的隶属函数分布,比如是一个三角形隶属函数
x = [1 2 3 4 5]; % 输出模糊集对应的x轴值
y = [0 0.5 1 0.5 0]; % 对应的隶属度值
% 使用中心平均解模糊化法进行去模糊化
defuzzified_value = trapz(x, y.*x) / trapz(x, y);
% 输出去模糊化后的结果
disp(['去模糊化后的值为: ', num2str(defuzzified_value)]);
上述代码中, trapz 函数用于计算数值积分,实现的是中心平均解模糊化方法。它通过计算隶属函数与x轴下面积的加权平均来得到一个确定的数值。
MATLAB中的去模糊化
MATLAB提供了专门的函数来进行去模糊化,例如 defuzz 函数,使用它可以让去模糊化的过程更简单。以下是如何使用 defuzz 函数的一个示例:
% 定义模糊集的隶属度函数
mf = trapmf(x, [1 2 3 4]); % 三角形隶属函数
% 应用defuzz函数进行去模糊化
defuzzified_value = defuzz(x, mf, 'centroid');
% 输出去模糊化后的结果
disp(['使用defuzz函数去模糊化后的值为: ', num2str(defuzzified_value)]);
在这个示例中, trapmf 函数用于创建三角形隶属函数, defuzz 函数则是用来计算这个模糊集的去模糊化值。参数 'centroid' 指定了去模糊化方法,即中心平均解模糊化法。
以上就是去模糊化的基本原理、步骤以及如何在MATLAB中实现去模糊化的详细介绍。去模糊化是模糊控制过程中的重要环节,它使得模糊控制器的输出可以被实际应用,这是模糊控制技术在工程领域广泛应用的基础。
简介:模糊控制算法,基于模糊逻辑的控制策略,在不确定性和非线性系统中有突出表现。本项目展示如何用纯MATLAB代码实现一个模糊控制系统,不依赖MATLAB系统函数,深入理解模糊逻辑和MATLAB编程。项目详细说明了模糊控制的基本思想,包括模糊化、规则推理和去模糊化三个主要步骤,并提供了关于系统设计的说明、实验数据以及功能块说明,有助于理解代码结构和工作流程。MATLAB中使用M文件编写了主控制程序和相关函数,为学习和应用模糊控制提供实践经验。
























 5429
5429

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








