N-gram统计语言模型(总结)

N-gram统计语言模型

1.统计语言模型

自然语言从它产生開始，逐渐演变成一种上下文相关的信息表达和传递的方式。因此让计算机处理自然语言。一个主要的问题就是为自然语言这样的上下文相关特性建立数学模型。

这个数学模型就是自然语言处理中常说的

统计语言模型 ， 它是今天 全部自然语言处理的基础 ，而且广泛应用与机器翻译、语音识别、印刷体和手写体识别、拼写纠错、汉字输入和文献查询。

2.N-Gram

N-Gram是大词汇连续语音识别中经常使用的一种语言模型。对中文而言，我们称之为汉语语言模型(CLM, Chinese Language Model)。汉语语言模型利用上下文中相邻词间的搭配信息，在须要把连续无空格的拼音、笔划，或代表字母或笔划的数字，转换成汉字串(即句子)时。能够计算出具有最大概率的句子，从而实现到汉字的自己主动转换。无需用户手动选择。避开了很多汉字相应一个同样的拼音(或笔划串，或数字串)的重码问题。

 搜狗拼音和微软拼音的主要思想就是N-gram模型的，只是在里面多增加了一些语言学规则而已。

3.用数学的方法描写叙述语言规律

美联储主席本.伯克南昨天告诉媒体7000亿美元的救助资金将借给上百家银行、保险公司和汽车公司。（这句话意非常通顺，意思也非常明确）

改变一些词的顺序。或者替换掉一些词，这句话变成：

本.伯克南美联储主席昨天7000亿美元的救助资金告诉媒体将借给银行、保险公司和汽车公司上百家。（意思就含混了，尽管多少还是能猜到一点）。

可是假设再换成：

联主美储席本.伯诉体南将借天的救克告媒助资金70元亿00美元给上百百百家银保行、汽车保险公司公司和。（基本上读者就不知所云了）。

20世纪70年代之前，科学家们试图推断这个文字序列是否合乎文法、含义是否正确等。但这条路走不动。贾里尼克从另外一个角度来看待这个问题。用一个简单的统计语言模型非常美丽的搞定了它。贾里尼克的出发点非常easy：一个句子是否合理。就看看它的可能性大小怎样。至于可能性就用概率来衡量。

第一个句子出现的概率最大，因此。第一个句子最有可能句子结构合理。这种方法更普通而严格的描写叙述是： 假定S表示某一个有意义的句子，由一连串特定顺序排列的词w1,w2,w3,...,wn组成。这里n是句子的长度。如今，我想知道S在文本中（语料库）出现的可能性，也就是数学上所说的S的概率P(S)。我们须要一个模型来估算概率。既然S=w1,w2,w3,...,wn。那么最好还是把P(S)展开表示： P(S)=P(w1,w2,w3,...,wn)

利用条件概率的公式。S这个序列出现的概率等于每个词出现的条件概率相乘,于是P(w1,...,wn)展开为：、

P(S)=P(W1,W2,W3,...,Wn)=P(W1)P(W2|W1)P(W3|W1,W2)…P(Wn|W1,W2,…,Wn-1)

当中P(w1)表示第一个词w1出现的概率；P(w2|w1)是已知第一个词的前提下。第二个词出现的概率；以此类推，词wn出现的概率取决于它前面全部的词。

补充知识：

条件概率、贝叶斯公式的具体解说

可是这样的方法存在两个致命的缺陷：一个缺陷是參数空间过大(条件概率P(wn|w1,w2,...,wn-1)的可能性太多，无法估算)，不可能有用化。另外一个缺陷是数据稀疏严重。

数据稀疏的解释：如果词表中有20000个词，如果是bigram model(二元模型)那么可能的2-gram就有400000000个，如果是trigram(3元模型)，那么可能的3-gram就有8000000000000个！

那么对于当中的非常多词对的组合，在语料库中都没有出现，依据最大似然估

计得到的概率将会是0。这会造成非常大的麻烦，在算句子的概率时一旦当中的某项为0。那么整个句子的概率就会为0，最后的结果是 ，我们的模型仅仅能算可怜兮兮的几个句子，而大部分的句子算得的概率是0. 因此，我们要进行数据平滑（data Smoothing），数据 平滑的目的有两个：一个是使全部的N-gram概率之和为1，使全部的N-gram概率都不为0,有关数据平滑处理的方法能够參考《数学之美》第33页的内容 。

4.马尔科夫如果

为了解决參数空间过大的问题。引入了马尔科夫如果：随意一个词的出现的概率只与它前面出现的有限的一个或者几个词有关。

如果一个词的出现的概率仅于它前面出现的一个词有关。那么我们就称之为bigram model(二元模型)。

即

   P(S) = P(W1,W2,W3,…,Wn)=P(W1)P(W2|W1)P(W3|W1,W2)…P(Wn|W1W2…Wn-1)
          ≈P(W1)P(W2|W1)P(W3|W2)…P(Wi)|P(Wi-1)...P(Wn|Wn-1)

 假设一个词的出现仅依赖于它前面出现的两个词，那么我们就称之为trigram（三元模型）。

在实践中用的最多的就是bigram和trigram了，并且效果非常不错。

高于四元的用的非常少，由于训练它（求出參数）须要更庞大的语料。并且数据稀疏严重，时间复杂度高，精度却提高的不多。当然，也能够如果一个词的出现由前面N-1个词决定，相应的模型略微复杂些，被称为N元模型。

5.怎样预计条件概率问题

条件概率推导在《数学之美》第30页有具体解说，在此讲述一个简单的条件概率。

一种简单的预计方法就是最大似然预计(Maximum Likelihood Estimate）了，即P(Wn|W1,W2,…,Wn-1) = (C(W1,W2,…,Wn)) / (C(W1, W2,…,Wn-1))     。

C(w1,w2,...,wn)即序列w1,w2,...,wn在语料库中出现的次数。

对于二元模型P(Wi|Wi-1)=C(Wi-1,Wi)/C(Wi-1)

（最大似然预计是一种统计方法，它用来求一个样本集的相关概率密度函数的參数，具体的解说点击打开链接）。

6.在一个语料库样例

注：这个语料库是英文的，而对于汉字语料库，须要对句子分词，才干做进一步的自然语言处理。

在训练语料库中统计序列C(W1 W2…Wn) 出现的次数和C(W1 W2…Wn-1)出现的次数。

 以下我们用bigram举个样例。如果语料库总词数为13,748

 

                       

   

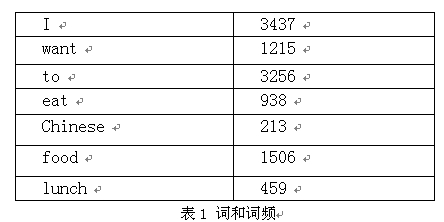
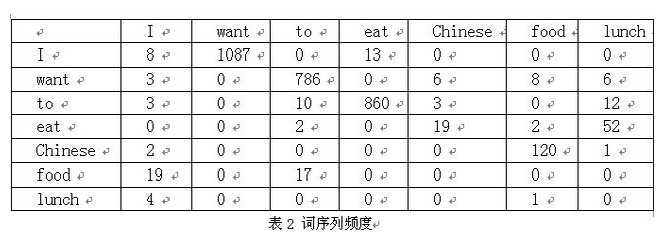
P(I want to eat Chinese food)
=P(I)*P(want|I)*P(to|want)*P(eat|to)*P(Chinese|eat)*P(food|Chinese)
=0.25*1087/3437*786/1215*860/3256*19/938*120/213
=0.000154171     

对与 I to Chinese want food eat 的概率远低于I want to eat Chinese food，所以后者句子结构更合理。

注：P(wang|I)=C(I want)|C(I)=1087/3437                                                                                                                      

网上非常多资料中，表1 词与词频和表2 词序列频度是没有的，所以造成文章表意不清。

对于 1).高阶语言模型  2).模型的训练、零概率问题和平滑方法 3).语料库的选取等问题，《数学之美》中都有具体解说，在此不再概述。

版权声明：本文博主原创文章，博客，未经同意不得转载。