目录
1.前言
自然语言(Natural Language)其实就是人类的语言,自然语言处理(NLP)就是对人类语言的处理,当然主要利用计算机。自然语言处理是关于计算机科学和语言学的交叉学科,常见的研究任务包括:
- 分词(Word Segmentation或Word Breaker,WB)
- 信息抽取(Information Extraction,IE):命名实体识别和关系抽取(Named Entity Recognition & Relation Extraction,NER)
- 词性标注(Part Of Speech Tagging,POS)
- 指代消解(Coreference Resolution)
- 句法分析(Parsing)
- 词义消歧(Word Sense Disambiguation,WSD)
- 语音识别(Speech Recognition)
- 语音合成(Text To Speech,TTS)
- 机器翻译(Machine Translation,MT)
- 自动文摘(Automatic Summarization)
- 问答系统(Question Answering)
- 自然语言理解(Natural Language Understanding)
- OCR
- 信息检索(Information Retrieval,IR)
早期的自然语言处理系统主要是基于人工撰写的规则,这种方法费时费力,且不能覆盖各种语言现象。上个世纪80年代后期,机器学习算法被引入到自然语言处理中,这要归功于不断提高的计算能力。研究主要集中在统计模型上,这种方法采用大规模的训练语料(corpus)对模型的参数进行自动的学习,和之前的基于规则的方法相比,这种方法更具鲁棒性。
在这个大背景下产出了统计机器学习方法和统计自然语言处理方法,包括今天提到的统计语言模型。
推荐以下两本很流行的关于统计学习的书:统计学习方法和统计自然语言处理

2. 什么是N-Gram模型
N-Gram是一种基于统计语言模型的算法。它的基本思想是将文本里面的内容按照字节进行大小为N的滑动窗口操作,形成了长度是N的字节片段序列。
每一个字节片段称为gram,对所有gram的出现频度进行统计,并且按照事先设定好的阈值进行过滤,形成关键gram列表,也就是这个文本的向量特征空间,列表中的每一种gram就是一个特征向量维度。
该模型基于这样一种假设,第N个词的出现只与前面N-1个词相关,而与其它任何词都不相关,整句的概率就是各个词出现概率的乘积。这些概率可以通过直接从语料中统计N个词同时出现的次数得到。常用的是二元的Bi-Gram和三元的Tri-Gram。
3.利用N-Gram模型评估语句是否合理
在介绍N-Gram模型在评估语句合理性这个应用之前,先看一个例子。
首先,从统计的角度来看,自然语言中的一个句子 s 可以由任何词构成,不过概率句子s出现的概率 有大有小。例如:
有大有小。例如:
 = 我刚吃过晚饭
= 我刚吃过晚饭 = 刚我过晚饭吃
= 刚我过晚饭吃
显然,对于中文而言 是一个通顺且有意义的句子,而
是一个通顺且有意义的句子,而 不是,所以对于中文来说,
不是,所以对于中文来说,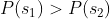 .但对于其他语言来说,概率值可能会出现反转。
.但对于其他语言来说,概率值可能会出现反转。
其次,另外一个例子是,如果我们给出了某个句子的一个节选,我们其实可以能够猜测后续的词应该是什么,例如
- the large green__. ('mountain' or 'tree'?)
- Kate swallowed the large green__.('pill' or 'broccoli'?)
显然,如果我们知道一个句子片段更多前面内容的情况下,我们会得到一个更加准确的答案。所以,前面的(历史)信息越多,对后面未知信息的约束就越强。
如果我们有一个由m个词组成的序列/句子s,即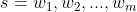 ,我们希望算的该句子出现的概率:
,我们希望算的该句子出现的概率:

上面这个联合概率链规则显然不好算,虽然它考虑了所有词和词之间的依赖关系,但是这样非常复杂,在实际中几乎没有办法使用。于是,我们需要用一种办法来近似这个公式,要求其效果要比独立性假设好(假设句子中每个词之间是独立的,没有任何关系,也就是下文中要提到的1-gram/uni-gram)。 这个办法就是著名的马尔可夫假设,即当前这个词仅仅跟前面几个有限的词相关,因此也就不必追溯到最开始的那个词,这样就可以大幅缩减上述算式的长度,即:
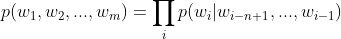
特别地,n取值比较小时,下面给出一元/2元/3元模型:
- 当n=1时,这是一个一元模型(独立性假设,各个词之间相互独立。1-gram/unigram)
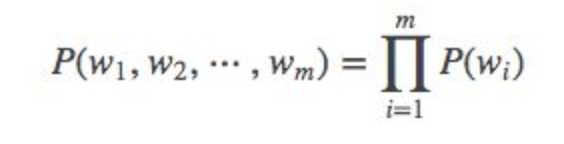
- 当n=2时,这是一个二元模型(2-gram/bigram):

- 当n=3时,这是一个三元模型(3-gram/trigram):

下面的思路就比较简单了,在给定的训练语料中,利用贝叶斯定理,将上述的条件概率值都统计计算出来即可,然后相乘就可以得到整个句子出现的概率。公式如下:
- 对于unigram来说,其中
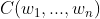 表示n-gram
表示n-gram 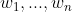 在训练语料中出现的次数,M是语料库中的总词数(如 对于yes,no,no,no,yes来说,M=5,以下符号都是同理)
在训练语料中出现的次数,M是语料库中的总词数(如 对于yes,no,no,no,yes来说,M=5,以下符号都是同理)








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 2686
2686

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








