微信红包的随机算法是怎样实现的？
RT。我考虑了一个简单的算法：
比如100元，由10个人分，那么平均一个人是10元钱。然后付款后，系统开始分份儿。
第一份：系统由0～10元之间随机一个数，作为这一份的钱数，设x1。
第二份：剩下的钱(100-x1)，系统由0～(100-x1)/(10-1)随机一个数，作为这份的钱数，设x2
.。。。
第n份：剩下的钱(100-x1-x2-...-xn)，系统由0~(100-x1-x2-...-xn-1)/(10-n)随机一个数，作为这个份的钱数，设为xn
当用户进来拿红包的时候，系统由0～9之间随机一个数，随机到几，就取第几份红包，然后将这个数存到list里。当之后的用户抽到相同的随机数时，则将这个数+1，如遇相同再+1，直至list满，红包发完。
------------------------------------------------
我这么实现可以么？？
或者大家有更好的办法？？？？修改
按投票排序按时间排序
41 个回答
赞同89反对，不会显示你的姓名
马景铖，关注基本问题，热爱土豆地瓜
楼上大多数人都是在做出自己的猜测，这也是在不知道内部随机算法的时候的唯一选择，但是大多数人没有给出自己亲自的调查结果。这里给出一份100样本的调查抽样样本数据，并提出自己的猜测。
1. 钱包钱数满足截尾正态随机数分布。大致为在截尾正态分布中取随机数，并用其求和数除以总价值，获得修正因子，再用修正因子乘上所有的随机数，得到红包价值。
这种分布意味着：低于平均值的红包多，但是离平均值不远；高于平均值的红包少，但是远大于平均值的红包偏多。
图1. 钱包价值与其频率分布直方图及其正态拟合
但看分布直方图并不能推出它符合正态分布，但是考虑到程序的简洁性和随机数的合理性，这是最合乎情理的一种猜测。
2. 越是后面的钱包，价值普遍更高
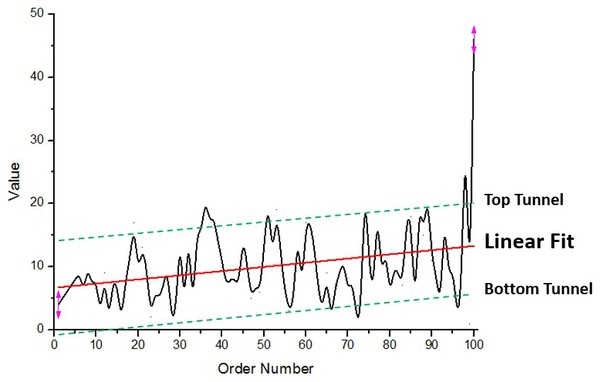
图2. 钱包序列数与其价值关系曲线
从图2中的线性拟合红线可以看到，钱包价值的总体变化趋势是在慢慢增大，其变化范围大约是一个绿色虚线上下界划出的“通道”。(曲线可以被围在这么一个正合乎常规的“通道”中，也从侧面反映了规律1的合理性，说明了并不是均匀分布的随机数)
从另一个平均数的图中也可以看出这一规律。
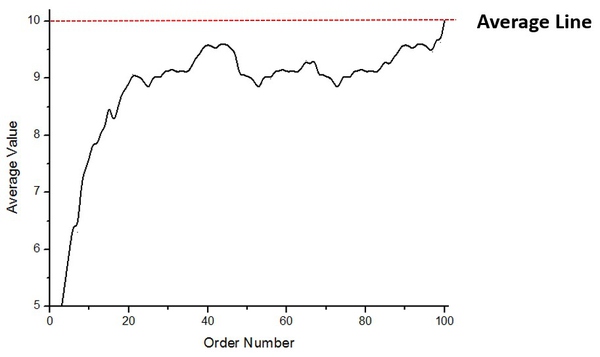
图3. 平均数随序列数的变化曲线
在样本中，1000价值的钱包被分成100份，均值为10。然而在图3中我们可以看到在最后一个钱包之前，平均数一直低于10，这就说明了一开始的钱包价值偏低，一直被后期的钱包价值拉着往上走，后期的钱包价值更高。
3. 当然平均数的图还可以透露出另一个规律，那就是最后的那一个人往往容易走运抽得比较多。因为最后那一个人是钱包剩下多少就拿多少的，而之前所有人的平均数都低于10，所以至少保证了最后一个人会高于平均值。在本样本中，98号钱包抽到35，而最后一份钱包抽到46。
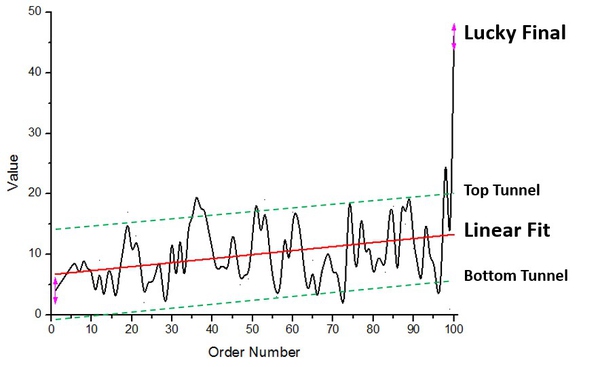
综上，根据样本猜测：
1. 抽到的钱大多数时候跟别人一样少，但一旦一多，就容易多很多。
2. 越是抽后面的钱包，钱越容易多。
3. 最后一个人往往容易撞大运。
其实这些一点用的没有，就是自己闲了无聊开一开脑洞，大家别认真，玩红包开心就好哈哈，土豆祝大家新年快乐啦~
——Potato
赞同13反对，不会显示你的姓名
王霄池，连快排都得换成 Haskell 才能背下来的战…
据观察，红包分钱满足以下几点：
不会有人拿不到钱
不会提前分完
钱的波动范围很大
@于野 的答案我完全同意。红包在一开始创建的时候，分配方案就订好了。抢红包的时候，不过是挨个pop up而已。
针对他说的算法二写个 python 代码。
def weixin_divide_hongbao(money, n):
divide_table = [random.randint(1, 10000) for x in xrange(0, n)]
sum_ = sum(divide_table)
return [x*money/sum_ for x in divide_table]
不过上述算法还有两个小问题：
浮点数精度问题
边界值的处理
不过，都是很容易解决的小问题，你们看的是算法思想，对吧。
赞同5反对，不会显示你的姓名
易敏恭，工程师
从工程角度来说，红包分配算法需要简单粗暴的实现。
楼上有人的算法过于复杂，第几个人领取都要面面俱到的计算，考虑因素太多，工程实现上真的没必要。
其实只需要按照如下框架即可：
1. 发红包时，按照设计的快速随机算法，将红包分好若干份。
2. 按照设计的评估算法，对得到的红包分配进行校验。
3. 如果校验不通过，如贫富差距过大，则重复随机分配。
4. 如果若干次重复，如5次，则停止重复，就按照当前分配。
5. 再有用户请求红包，直接队列化请求，再从红包序列中取出对应编号红包。
上述方案的优势是：
1. 只需“一次”计算。
随机算法选择简单粗暴的即可，系统按照校验策略对其评价，不满足则有限次重复，直到满足或次数太多为止。
2. 此后就只有读取。
后续操作完全是读取缓存，无需密集计算。
那么是不是还有更简单粗暴的方案呢？还是有的，那就是伪随机序列查表法。
百万千万级别的红包请求，如果每次都按照真随机来计算，仍然会有不小的计算压力。
索性预先计算得到若干伪随机分配方案，调用时只需要随机选择一个即可。
举例来说，有人的红包是10元分配给5人，系统预先存有多种分配方案，如1，1，2，3，3，或1，1，2，2，4，请求时随机选取一个方案即可。
当然，各种组合未必能穷尽，但是只需要让用户在有限次操作中觉得这是随机就够了。
赞同31反对，不会显示你的姓名
InnerNight，非典型码农
我觉得这个问题的合理解有两个目标：1. 不要出现人为的阈值，比如预留值、最大和最少量、切割比例等拍脑袋的数据。2.尽量贴近过年的喜庆气氛，不要出现太多或者太少的情况。如果有什么其它考虑，方便实现成代码也算一个。
所以我的思路其实用一句话就可以概括：生成n（n是总人数）个(0，1]之间的随机数，然后将其求和被Q(Q是总钱数)除得到一个比例C，用C乘以所有数，这样就得到了最终结果。
这个算法很多人都会想到，但是被大家抛弃的原因应该在于随机性太大。那么我想到的修正方案：生成随机数时不要采用平均分布的随机数，而用正态分布的随机数。可是系统提供的随机数算法基本都是基于平均分布的，那现在提供一个平均分布映射到正态分布的算法就可以了。其实这个算法很常见，假设生成的平均分布数是x，正态分布所求值是y，正太分布表达式是f(y)，那么f(y)求积分记为F(y)，根据这样一个式子F(y) = x，求出F(y)的反函数就是所需要的映射函数。这个看起来很复杂，其实求出一个式子后代码写起来很简单。原谅我的数学表达基本已经都忘了，如果有写错，欢迎指正。
所以这个算法只需要两个function就可以实现，下面是个伪代码 :
double generateRandomNumber(){
//generate random number based on normal distribution
}
void process(double totalMoney, int personNum){
double[personNum] results;
for (int i=0; i < personNum; i++){
results[i] = generateRandomNumber();
}
double ratio = totoalMoney/sum(results);
for (int i=0; i < personNum; i++){
results[i] = result[i] * ratio;
}
}
PS：这个算法的生产随机数其实是可配置的，取决于开发者希望最终趋近于什么样的分布，只要找到其和平均分布的映射关系，就可以使用什么样的生成算法。
PPS：这个分布算法如果能让用户配置会更好玩，比如配置成1个人领50%，3个人领30%，剩下的人分20%，还会有抽大奖的感觉，哈哈哈~
赞同5反对，不会显示你的姓名
粑卜狸
在看数据之前，我先说说自己的想法：
1. 把钱看成连续的，分完以后再修正bug：a）为了使最小单位为0.01，最后结果精确到十分位即可，零头全部倒给最后一个人（或者从最后一个人那里出）b）如果有人说万一出现有人为0或者负数怎么办，这好办，一开始先给每人分配0.01作为“底钱”就好了。
2. @马景铖的猜想是基于调查数据的，这点我非常赞赏。不过想提出一点意见（不好意思大过年的较真了哈哈）：图2用线性回归做趋势分析是很好的，不过应该给出置信区间或p值等统计显著性指标。图3其实是有些误导的，因为你做的是一个累计平均，误差近似于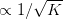
，所以如果你把Confidence Band画出来也许会发现并没有显著偏离平均值。
3. 对于这个问题，大家可能关心两个问题：a）算法怎么实现的？b）先拿好还是后拿好？我认为后一个问题比较好回答，而且顺便想指出的是，即使存在和次序相关的“bug”，也非常容易“修正”：每次生成完分配方案以后把顺序打乱即可。
现在说说我是怎么分析这个问题的：
1. 首先同样是采样。我从微信群里抓取了37次分红的结果，为了使样本具有可比性，我只筛选了分红人数为5的样本，数据（一共37行）大概长这样：
[,1] [,2] [,3] [,4] [,5]
[1,] 0.26 1.64 1.50 0.51 1.09
[2,] 0.16 1.20 1.28 2.03 1.21
[3,] 0.03 0.43 0.01 0.51 0.02
[4,] 5.39 2.67 1.74 3.27 1.93
[5,] 0.31 0.07 0.07 0.33 0.22
[6,] 0.44 1.93 1.40 1.72 3.39
...
其中每一行是一次分红。例如：抽样的第三个红包总金额为1元，其中第2个人抽到了0.43元。
2. 然后一个我认为合理的假设（其实可能大家都已经默认了）是：我们的分布是齐次的。
记每个人分红的联合分布密度函数（joint pdf）为
，其中
是第
个人分到的金额（在我们的数据中
），而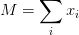
为总金额。那么齐次指的是：
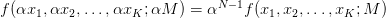。用通俗的语言说一遍就是：如果你把总金额乘上一个倍数，新的分布和原来的分布是“相似”的。
3. 有了齐次的假设，我们就可以把采集到的数据归一化（每一行除以它们的和），得到的每一个结果的意义是：每个人分到的钱占总金额的比例。
4. 箱形图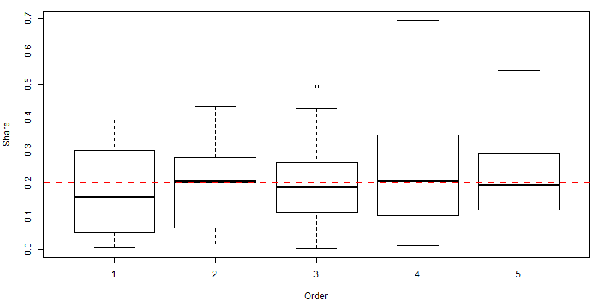
上图是37个样本的总结（横轴代表第几个人，纵轴是分到的比例）。从这幅图来看看不出啥，不过别急，这张图并不完全适合描述我们这个问题，因为每一个人的分红是相关的。
4. 直方图
没有评论。
5. 图上面我没看出啥明显的端倪，数字呢？
五组的均值：0.1704179 0.1915872 0.1899119 0.2418445 0.2062385
另外给出协方差矩阵：
V1 V2 V3 V4 V5
V1 0.0165548015 -0.005619991 0.0009090151 -0.009668083 -0.002175743
V2 -0.0056199905 0.015760475 -0.0017319045 -0.004626603 -0.003781977
V3 0.0009090151 -0.001731904 0.0149705394 -0.010626132 -0.003521518
V4 -0.0096680832 -0.004626603 -0.0106261322 0.031287609 -0.006366791
V5 -0.0021757429 -0.003781977 -0.0035215178 -0.006366791 0.015846028
协相关矩阵（以后会用到）：
V1 V2 V3 V4 V5
V1 1.00000000 -0.3479277 0.05774181 -0.4248075 -0.1343338
V2 -0.34792765 1.0000000 -0.11275104 -0.2083490 -0.2393172
V3 0.05774181 -0.1127510 1.00000000 -0.4909873 -0.2286393
V4 -0.42480752 -0.2083490 -0.49098735 1.0000000 -0.2859395
V5 -0.13433382 -0.2393172 -0.22863934 -0.2859395 1.0000000
我们做一个Wald test，看看我们的数据是不是满足零假设（五组的期望均为0.2），略去计算过程，Wald test statistic = 0.0878， p值约为1，说明没有显著证据拒绝零假设。因此回答了问题b）先拿好还是后拿好？——都一样（从目前数据看来）。
6. 从经验分布反推模型是一个比较玄的事情，我们可以通过一些检验（正态检验、卡方检验）来从统计学上排除某个分布，但没有人能告诉你哪个分布是“对”的（All models are wrong, but some are useful. -- George E. P. Box）。可能和强迫症有关系，这个截断正态分布在我看来并不是一个漂亮的模型。狄利克雷分布（参见Dirichlet distribution）可能是个更好的选择：它要求这K个随机变量分布在0~1之间，且它们的和为1，这正是我们想要的！进一步想，既然目前没有明显证据支持每个人分到的比例不相同，那就从零假设（相同）出发。对于狄利克雷分布而言，就是所有的a（公式编辑器突然坏了，所以不写tex了，想看的去Wiki上找）都相同，代入到Dirichlet distribution页面中关于期望和方差的公式（K=5）得到E[Xi]=0.2，Var[Xi]=4/[25(5a+1)]，Cor[Xi,Xj]=-0.25。和之前我们看到的数字（均值、方差、协相关）比是不是有一点点像？
7. 这是拟合的结果，拟合出的系数a（分别）为1.050646 1.237996 1.161214 1.443003 1.352875。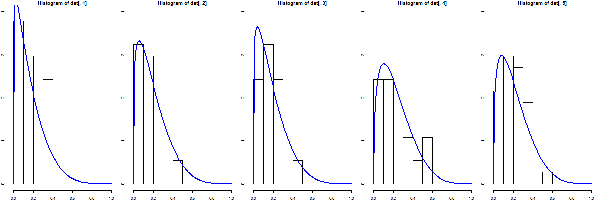
我相信，如果有更多的数据，我们可以更有把握（power）地判断a是否有显著区别，或者说，第几个拿最好？
赞同15反对，不会显示你的姓名
匿名用户
转。
微信是采用什么样的算法做到的？简单百度了下，目前尚未有官方的说明，仅仅在知乎里有一个较为热门的讨论，链接戳这里 不过他们讨论的太过于深入，有掉坑之嫌。
我按照自己的逻辑尝试了下，这个算法需要满足以下几点要求
1、每个人都要能够领取到红包；2、每个人领取到的红包金额总和=总金额；3、每个人领取到的红包金额不等，但也不能差的太离谱，不然就没趣味；4、算法一定要简单，不然对不起腾讯这个招牌；
正式编码之前，先搭建一个递进的模型来分析规律
设定总金额为10元，有N个人随机领取： N=1 则红包金额=X元； N=2 为保证第二个红包可以正常发出，第一个红包金额=0.01至9.99之间的某个随机数 第二个红包=10-第一个红包金额； N=3 红包1=0.01至0.98之间的某个随机数 红包2=0.01至(10-红包1-0.01)的某个随机数 红包3=10-红包1-红包2 ……
至此，规律出现啦！开始编码！
header("Content-Type: text/html;charset=utf-8");//输出不乱码，你懂的 $total=10;//红包总额 $num=8;// 分成8个红包，支持8人随机领取 $min=0.01;//每个人最少能收到0.01元 for ($i=1;$i<$num;$i++) { $safe_total=$total-($num-$i)*$min;//随机安全上限 $money=mt_rand($min*100,$safe_total*100)/100; $total=$total-$money; echo '第'.$i.'个红包：'.$money.' 元，余额：'.$total.' 元 <br/>'; } echo '第'.$num.'个红包：'.$total.' 元，余额：0 元';
输入一看，波动太大，这数据太无趣了！
第1个红包：7.48 元，余额：2.52 元 第2个红包：1.9 元，余额：0.62 元 第3个红包：0.49 元，余额：0.13 元 第4个红包：0.04 元，余额：0.09 元 第5个红包：0.03 元，余额：0.06 元 第6个红包：0.03 元，余额：0.03 元 第7个红包：0.01 元，余额：0.02 元 第8个红包：0.02 元，余额：0 元
改良一下，将平均值作为随机安全上限来控制波动差
header("Content-Type: text/html;charset=utf-8");//输出不乱码，你懂的 $total=10;//红包总额 $num=8;// 分成8个红包，支持8人随机领取 $min=0.01;//每个人最少能收到0.01元 for ($i=1;$i<$num;$i++) { $safe_total=($total-($num-$i)*$min)/($num-$i);//随机安全上限 $money=mt_rand($min*100,$safe_total*100)/100; $total=$total-$money; echo '第'.$i.'个红包：'.$money.' 元，余额：'.$total.' 元 <br/>'; } echo '第'.$num.'个红包：'.$total.' 元，余额：0 元';
输出结果见下图
第1个红包：0.06 元，余额：9.94 元 第2个红包：1.55 元，余额：8.39 元 第3个红包：0.25 元，余额：8.14 元 第4个红包：0.98 元，余额：7.16 元 第5个红包：1.88 元，余额：5.28 元 第6个红包：1.92 元，余额：3.36 元 第7个红包：2.98 元，余额：0.38 元 第8个红包：0.38 元，余额：0 元
如果你有更好更简单的算法，欢迎与我讨论。
作者：Small
链接：微信红包的算法实现探讨
﹣﹣﹣﹣﹣ java version ﹣﹣﹣﹣﹣
/** * 微信红包分配算法 * * @author Michael282694 * */ public class wechat_money { public static void main(String[] args) { // TODO Auto-generated method stub double total_money; // 红包总金额 int total_people; // 抢红包总人数 double min_money; // 每个人最少能收到0.01元 total_money = 10.0; total_people = 8; min_money = 0.01; for (int i = 0; i < total_people - 1; i++) { int j = i + 1; double safe_money = (total_money - (total_people - j) * min_money) / (total_people - j); double tmp_money = (Math.random() * (safe_money * 100 - min_money * 100) + min_money * 100) / 100; total_money = total_money - tmp_money; System.out.format("第 %d 个红包： %.2f 元，剩下： %.2f 元\n", j, tmp_money, total_money); } System.out.format("第 %d 个红包： %.2f 元，剩下： 0 元\n", total_people, total_money); } }
某一次的結果：
第 1 个红包： 0.54 元，剩下： 9.46 元 第 2 个红包： 1.04 元，剩下： 8.42 元 第 3 个红包： 0.60 元，剩下： 7.83 元 第 4 个红包： 0.17 元，剩下： 7.66 元 第 5 个红包： 1.54 元，剩下： 6.11 元 第 6 个红包： 0.58 元，剩下： 5.53 元 第 7 个红包： 3.60 元，剩下： 1.93 元 第 8 个红包： 1.93 元，剩下： 0 元
7070
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
