《逻辑与计算机设计基础（原书第5版）》——2.2 布尔代数

2.2　布尔代数

布尔代数是一种用来处理二进制变量和逻辑运算的代数方法。变量用大写字母来表示，三种基本的逻辑运算分别是与、或、非（取反）。布尔表达式（Boolean expression）是一个由二进制变量、常量0和1、逻辑运算符号和括号等组成的代数运算式。布尔函数（Boolean function）可以描述为一个布尔等式，其中依次包括一个代表函数的二进制变量、一个等号以及一个布尔表达式。另外，函数标识符后面的括号里面包含一个用逗号分隔的函数变量列表。一个单输出的布尔函数（single-output Boolean function）是函数变量0和1的每一种可能组合到输出0或1的映射。一个多输出的布尔函数（multiple-output Boolean function）是函数变量0和1的每一种可能组合到输出0和1的组合的映射。
例2-1　布尔函数举例—电动车窗
我们来看一个以布尔等式表示的电气或电子逻辑控制的例子—汽车的电动车窗。
L(D, X, A)＝DX＋A
车窗的升降由一个马达来控制，这个马达驱动一个连接到车窗的升降机构。函数值L＝1时，车窗马达通电使车窗降下来，L＝0时则不能使车窗降下。D是一个由车内司机那一侧门上的一个开关控制的输出。当D＝1时，发出使车窗降下的指令，当D＝0时，则不发出车窗降下的指令。X是一个机械限位开关的输出，如果车窗处在极限位置，即车窗完全落下时，X＝1。如果车窗不在极限位置，即车窗还没有完全落下，则X＝0。A＝1时，表示车窗正在下降，直到其到达最下面的位置。A信号由一个定时逻辑产生，D和X是该定时逻辑的输入。只要D持续为1至少0.5s，A就变为1，并一直保持到X＝1。如果D＝1的持续时间少于0.5s，则A＝0。因此，如果司机发出使车窗下降的指令持续0.5s或更久，车窗就会自动降至最低位置。
表达式的两个部分DX和A称为表达式L的项（term）。当项DX为1或者项A＝1的时候，函数L为1，其他情况下，函数L为0。取反运算意味着，如果X＝1，则X＝0。所以，我们可以说：当满足D＝1且X＝0，或者满足A＝1时，L＝1。那么等式L如何用语言来描述呢？可以这样来描述：如果车窗没有完全降下来（X＝0）且开关D是按下的（D＝1），或者车窗将要自动下降到最低位置（A＝1），则车窗将会下降。 ■
布尔等式表示二进制变量之间的逻辑关系，它由等式中二进制变量取值的所有可能组合确定。布尔函数可以用真值表来表示。函数的真值表（truth table）列出了变量取值0和1的所有组合以及对应每一种组合的函数值。表2-1给出的逻辑运算的真值表是布尔函数的一些特殊情况。真值表的行数为2n，其中n是函数中二进制变量的个数。真值表中二进制组合的个数等于n位长二进制数的个数，对应的十进制数是0～2n-1。表2-5是函数L＝DX＋A的真值表，从中可以看出二进制变量D、X和A有8种可能的组合，L列的值对于每一种组合只有0或1。这个真值表显示，如果D＝1且X＝0，或者A＝1，则函数L的值为1，其他情况下函数L的值等于0。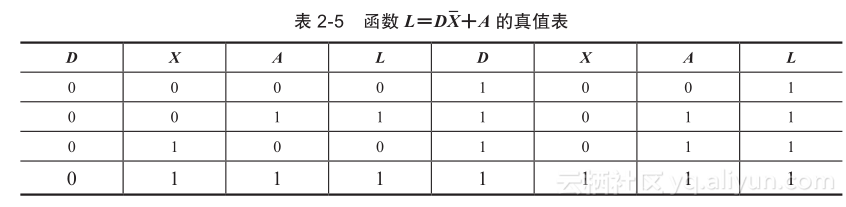

布尔函数的代数表达式可以转换为由逻辑门组成的能够实现其功能的电路图形式。函数L的逻辑电路图如图2-5所示，与电路等效的Verilog和VHDL模型如图2-6和图2-7所示。输入端X加一个反相器以产生X，与门对X和D进行运算，或门又将DX和A组合在一起。在逻辑电路图中，函数F的变量作为电路的输入，二进制变量F作为电路的输出。如果电路只有一个输出，则F是单输出函数。如果电路有多个输出，则函数F是有多个变量和多个用来表示输出的等式的多输出函数。门电路之间用导线连接在一起，导线用来传输逻辑信号，这种类型的逻辑电路称为组合逻辑电路（combinational logic circuit），因为变量通过逻辑运算进行“组合”。与此不同的是，时序逻辑的变量不仅可以随时组合还可以存储，时序逻辑将在第4章介绍。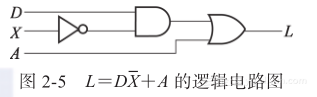

用真值表来表示布尔函数的方法只有一种。然而，当函数用代数方程来表示时可以有多种方式。表示函数的一个特定表达式常用来表示电路图中逻辑门之间的连接关系。通过布尔代数的运算法则可以改变布尔表达式的形式，因此对于同一个函数常常可能得到一个简单表达式。简单形式的布尔表达式不但可以减少电路中门电路的数量，而且可以减少门电路输入端的数量。要了解这是如何实现的，我们就必须首先学习布尔代数的基本法则。
2.2.1　布尔代数的基本恒等式
表2-6中所示的是布尔代数最基本的恒等式。只要不会引起混淆，我们就可以省略与运算符以使表示简单化。前面9个恒等式列出了单个变量X、X的补数X和二进制常量0、1之间的运算关系。后面5个恒等式（10～14）在一般代数中也有类似的情况。最后3个恒等式（15～17）虽然不能应用在一般代数中，但对于布尔表达式化简很有用。
表中的基本规则分成两列，以表示布尔代数的对偶特性。一个布尔表达式的对偶式（dual）可以通过交换与和或运算，用1替换0和用0替换1来获得。表中某一列的任意一个等式可以由另一列对应等式通过在其等号两边同时取对偶而得到。例如，关系式2是关系式1的对偶，因为关系式2中的或运算已经替换成了与运算，0也替换成了1。但要注意的是，在大多数情况下，一个表达式的对偶式并不等于原来的表达式，所以一个表达式通常不能用它的对偶式来代替。

表中只包含一个变量的9个恒等式，都可以很容易地用0或1替代X来加以验证。例如，证明X＋0＝X，假设X＝0，则0＋0＝0；假设X＝1则1＋0＝1。这两个等式符合或逻辑运算法则，所以是正确的。表中任何一个布尔等式中的X都可以用一个表达式来代替，因此，用X＝AB＋C代替恒等式3中的X，可以得到
AB＋C＋1＝1
注意，恒等式9将变量取反两次后使变量恢复到原来的值，因此如果X＝0，则X＝1，X＝0＝X。
恒等式10和11表示的是交换律，这表明在或运算和与运算中交换变量的位置不会影响运算结果。恒等式12和13所示的是结合律，它说明对三个变量进行运算的结果与先对哪个变量、后对哪个变量进行运算没有关系，因此括号可以全部消去，如下所示：
X＋(Y＋Z)＝(X＋Y)＋Z＝X＋Y＋Z
X(YZ)＝(XY)Z＝XYZ
这两个定律和第一个分配律（即性质14）在普通代数中也是众所周知的，所以它们很容易理解。由恒等式15所示的第二个分配律是普通分配律的对偶式，它在普通代数中并不成立。如前所述，各个恒等式中的每个变量都可以用布尔表达式来替代，而恒等式却仍然成立。考虑表达式（A＋B）（A＋CD），假设X＝A，Y＝B，Z＝CD，应用第二个分配律，我们可以得到
（A＋B）（A＋CD）＝A＋BCD
表2-6中的最后两个恒等式

是德摩根定理，这是个非常重要的定理，可以用来求一个表达式和对应函数的互补形式。通过列出二进制变量X和Y的所有组合，真值表可以用来说明德摩根定理。表2-7中的两个真值表证明了德摩根定理的第一部分。在真值表a中，我们针对X和Y的所有可能值计算了。计算的方法是先计算X＋Y，然后再对所得到的结果取反。在真值表b中，我们先计算X和Y，然后再将所得到的值进行与运算。对应X和Y的4种组合，两种运算的结果相同，这样便验证了等式的正确性。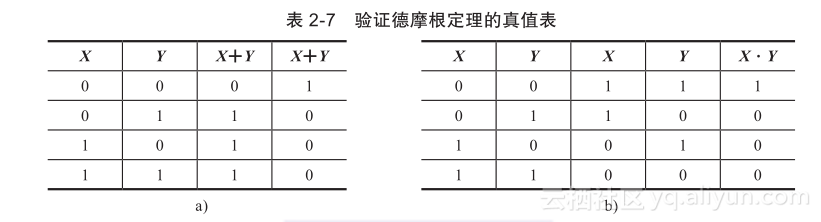

在计算等式的时候，要注意运算的顺序。在真值表b中，首先对变量进行取反运算，然后再进行与运算，就像普通代数运算中进行乘法和加法运算一样。在真值表a中，首先进行或运算，然后将得到的结果取反。将表达式X＋Y取反可以表示成非（X＋Y），计算括号里的表达式，并对其结果取反。如果表达式的上面用一杠来表示取反符号，我们习惯于去掉括号，因为这一杠已经把整个表达式连接在了一起。这样，（）可以用来表示。
德摩根定理可以扩展到三变量或多变量。通常德摩根定理可以表示为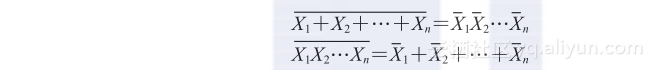

观察上面的逻辑运算可知，就是将或运算变换成与运算，与运算变换成或运算。另外，去掉对整个表达式的取反，而是对每一个变量分别取反。例如

2.2.2　代数运算
布尔代数是简化数字电路的有效工具。例如，考虑由下式表示的布尔函数

图2-8a所示的是用逻辑门来实现这个等式的电路。输入变量X和Z通过反相器取反变成X和Z，表达式中的三项用三个与门来实现，或门构成这三项的逻辑或。现在通过使用表2-6中的一些恒等式来简化表达式F。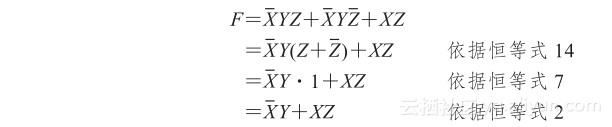

表达式被简化成仅有两项，可以用图2-8b所示的电路来实现。明显可以看出图2-8b中的电路比图2-8a中的电路简单，但它们能实现同一功能。通过真值表可以验证这两种方法是等效的，如表2-8所示。在图2-8a中，如果X＝0，Y＝1，Z＝1或者X＝0，Y＝1，Z＝0或者X＝Z＝1，则函数值为1，所以表中a部分的F有4个1。在图2-8b中，如果X＝0，Y＝1或者X＝1，Z＝1，则函数值为1，表中b部分的F有4个同样的1。因为这两个表达式生成了相同的真值表，所以这两个表达式是等效的。因此，两个电路的三个输入端输入相同的二进制变量，其输出结果是一样的。虽然每个电路实现了相同的功能，但使用门数少并且（或者）门输入少的电路更可取，因为它需要较少的元器件。

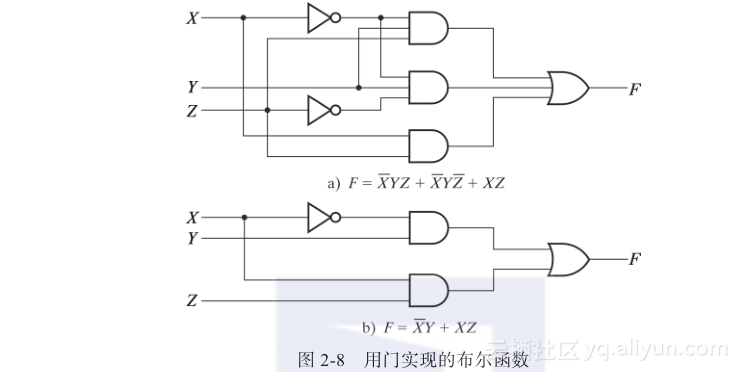
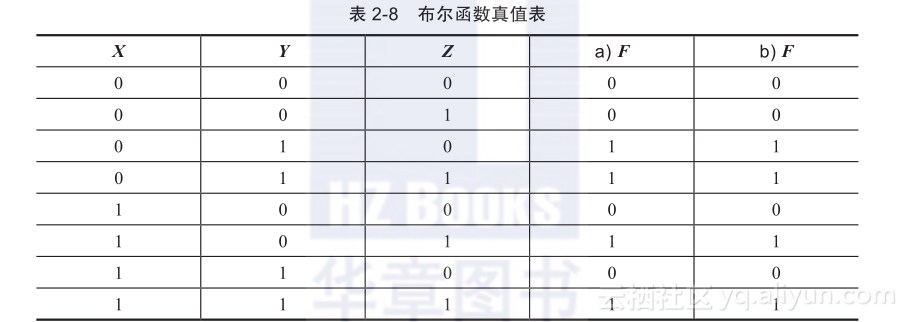
当一个布尔等式用逻辑门实现时，每一个项都需要用一个门，项中的每一个变量都对应着门的一个输入。我们将项中的一个变量或变量的补定义为字符（literal）。图2-8a所示函数的表达式中有3个项和8个变量，图2-8b中有2个项和4个变量。通过减少布尔表达式中项的数目、变量的数目或者同时减少两者，通常可以得到一个比较简单的电路。布尔代数的应用就是为了精简表达式以便得到简单的电路。对于高度复杂的函数，通过统计项和变量的数目来获得最好的表达式是很困难的，即使是使用计算机程序来进行处理。在关于逻辑电路综合的计算机工具中，经常会介绍一些简化表达式的方法。这些方法虽然不是最好的，但可以得到好的结果。一般情况下的人工方式是，使用我们熟知的基本定理和其他处理进行试探。下面的例子通过使用表2-6中的性质来举例说明一些可行的方法。
1）X＋XY＝X·1＋XY＝X(1+Y)＝X·1＝X
2）XY＋XY＝X＝X(Y＋Y)＝X·1＝X
3）X＋XY＝(X＋X)(X＋Y)＝1·(X＋Y)＝X＋Y
注意，中间的步骤X＝X×1和X×1＝X经常被省略，因为这很明显。关系式1＋Y＝1对于消除多余的项非常有用，就像在这个等式中消除项XY那样。关系Y＋Y＝1经常用于合并两个项，如等式2）所示。两个合并的项除一个变量外其他变量均相同，这个变量必须在一个项中取反，而在另一个项中不取反。等式3）的化简运用了分配律的第二种形式（表2-6中的性质15）。下面是另外三个布尔表达式化简的例子。
4）X(X＋Y)＝X·X＋X·Y＝X＋XY＝X(1＋Y)＝X·1＝X
5）(X＋Y)(X＋Y)＝X＋YY＝X＋0＝X
6）X(X＋Y)＝XX＋XY＝0＋YX＝YX
以上每一行，由第一个和最后一个表达式分别构成的6个等式是用表2-6中的性质推导出来的布尔代数定理，这些定理可以和表2-6中的性质一起使用来推导出更多的结果，也可以用来帮助进行化简。
定理4～6是等式1）～3）的对偶式。记住，求一个表达式的对偶式就是把与变为或，把或变为与（1变为0，0变为1，如果它们也在表达式中出现的话）。布尔代数的对偶原则（duality principle）指出，如果我们将表达式等号两边同时取对偶，则布尔等式依然是成立的。因此，等式4）、5）和6）可以通过对等式1）、2）和3）分别取对偶式而得到。
利用等式1）～6）所给出的结果，接下来介绍的一致律定理（consensus theorem）在布尔表达式的化简中非常有用：
XY＋XZ＋YZ＝XY＋XZ
由这个定理可以知道第三项YZ是冗余项，可以去掉。注意，Y和Z分别在前二项与X和X组合，在被去掉的那一项中一起出现。一致律定理可以通过把YZ项和（X＋X）＝1相与来进行证明，步骤如下：

一致律的对偶式如下：
(X＋Y)(X＋Z)(Y＋Z)＝(X＋Y)(X＋Z)
下面的例子表明怎样运用一致律来处理布尔表达式：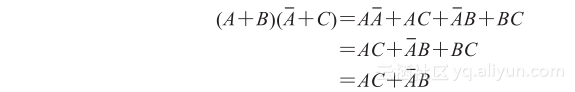

注意，AA＝0和0＋AC＝AC，运用一致律可以在最后一步去掉冗余项BC。
2.2.3　反函数
函数F的反函数F，就是在真值表中将F的值由1变成0，0变成1。函数取反的方法源于布尔代数中德摩根定理的使用，这个定理的一般表述就是，对表达式取反可以通过将与运算和或运算相互交换、将每一个变量和常量均取反的方法得到，如例2-2所示。
例2-2　对函数取反
求等式F1＝XYZ＋XYZ和等式F2＝X(YZ＋YZ)的反函数。多次运用德摩根定理，我们可以得到其反函数如下：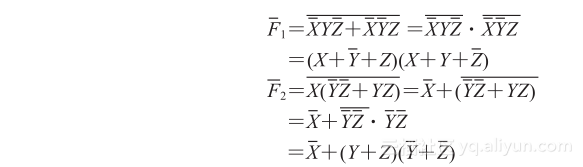

求反函数的一个简单方法是，求此函数的对偶式并将每一个文字变反，该方法与德摩根定理相符。记住，一个表达式的对偶式就是将与运算和或运算相互交换，1和0相互交换。在求复杂函数的对偶式之前可以通过添加括号来避免运算顺序的混淆，如例2-3所示。 ■
例2-3　用对偶式求反函数
求例2-2所示函数的反函数，要求先求对偶式，然后对每一个文字求反。
我们从下式开始
F1＝XYZ＋XYZ＝(XYZ)＋(XYZ)
F1的对偶式是
(X＋Y＋Z)(X＋Y＋Z)
对每一个文字取反可以得到
(X＋Y＋Z)(X＋Y＋Z)＝F1
现在
F2＝X(YZ＋YZ)＝X((YZ)＋(YZ))
F2的对偶式为
X＋(Y＋Z)(Y＋Z)
将每个文字取反得到

            　 X＋(Y＋Z)(Y＋Z)＝F2                     ■