小数除以小数的竖式题_教学设计丨除数是小数的除法

_	_	_	_
	“小数连心”，本着“相互交流、共同进步”的原则，公众号将推出学员的阅读感悟、教学心得、教学研究、教育叙事等优秀作品，搭建交流平台，共享研究成果。 公众号在每月5、15、25日(三·五)固定日推送，其他时间不定期推送，欢迎关注。
	_	_

向你介绍我是谁

陈丽娜，温州市龙湾区永中第一小学，温州市教坛新秀，龙湾区小学数学教研员王小莲工作室第六小组成员。

1.学情分析

学生已在四年级上学期学过商不变规律，本课之前已经学会了除数是整数的小数除法。除数是小数的除法，是一节计算课，对算理的理解、竖式的写法都是学生第一次接触。本节课如果按照教材的顺序教学，学生就会学得很枯燥，教师也会很疲惫，算理的理解不会很透彻，计算也不会扎实。要避免这些弊端，就要合理地设计教学，精心预设学生的想法。

2.设计理念

1.计算教学课是单调的、无味的、枯燥的。通过发红包的情境，再结合图形几何直观，让孩子去理解人民币之间的转化以及商不变性质。这样做不仅激发孩子的学习兴趣和欲望，还有利于理解它的算理。

2.发现高段的孩子都喜欢用笔算的方法去口算，翻看所有版本的教材，所有的口算教学都是安排在第一个课时，而在教学笔算时基本没有教口算方法。所以这节课教笔算之前先教口算。口算方法是理解算理的过程，教给孩子一种方法，口算与笔算的结合更有利于算理的理解，打通之间的关系。

3.“转化”的数学思想贯穿始终。

3.学习目标

教学目标：

    1.理解除数是小数的除法的算理。

    2.掌握一个数除以小数的计算方法，并能正确计算。

    3.在自主探索、合作交流的过程中培养学生的分析、转化及归纳的能力。

重点：理解算理、掌握算法。

难点：当被除数、除数的小数位数不同时，以除数为标准转化为除数是整数的除法。

4.过程预设

一、红包激趣，复习旧知

     1.出示微信红包，如图1。5.4元，发给3个人，每个人多少钱？

 预设：生1：口算解决；生2：列竖式解决 

 2.小结：这是前几节课我们学过的除数是整数的除法，在计算时要注意商的小数点要和被除数的小数点对齐。

   【设计意图：通过发红包的情境，激发了孩子学习兴趣和欲望，也可以唤起学生对除数是整数的除法的回忆。】

二、理解算理、讨论算法

   (一)解决问题，展示口算方法

    1. 继续发微信红包，如图2。还是5.4元，现在每个人发0.3元，能发给几个人？追问：你是怎么算的？

预设：

生1：单位转换 5.4元=54角   0.3元=3角  54÷3=18(个)

生2：商不变性质 5.4÷0.3=54÷3=18(个)

生3：从小数的意义去考虑，如图

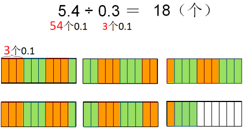
2.针对图，课件直观演示。

3.这三种口算方法，是不是都有共同的地方？

4.小结：都是把5.4除以0.3，转化成54除以3。我们班同学厉害，一个数除以小数，我们没学过，但我们能用已有的知识去转化它。

【设计意图：继续通过发红包的情境，再结合图形几何直观，数形结合，让孩子去理解人民币之间的转化以及商不变性质。本环节设计了教笔算之前先教口算，口算方法是理解算理的过程，教给孩子一种方法，口算与笔算的结合更有利于算理的理解，打通之间的关系。】

   (二)明确算理，尝试竖式书写

    1. 5.4÷0.3用竖式表示，学生自主尝试。

    2. 展示学生作品

 ①指着图4，前面口算结果是18，现在是1.8，到底答案是多少？

②指着图5，看不到你扩大了，能不能在竖式上也让别人一眼就看到你把它扩大了。

   (三)规范竖式，比较新旧联系

     1.黑板上板演正确竖式的书写。

边演示边引导：我们先把除数0.3扩大到它的10倍，也就是小数点向右移动一位，变成整数3。这时候，把0和小数点划掉，接着我们再把被除数5.4扩大到它的10倍，也就是小数点向右移动一位，变成整数54。这时候，也把小数点划掉。看，这个过程既能体现转化的过程，也不改变原式，是不时很完美。

    2.第一次比较：今天和上节课学的，有什么不同？

    3.揭题：这就今天要学的新知识。除数是小数的除法。

   【设计意图：让学生自主尝试去列竖式，展示多种方法，在对比中冲突、感悟，正确的竖式书写，并理解了算理。教师示范、演示移动小数点，板书竖式，呈现规范的书写格式，体现了引导作用。】

   (四)优化算法，对接前后知识

    1.尝试除数小数位数多于被除数小数位数的竖式

    ①再次发微信红包，如图7。6.4元，每个红包发0.16元，能发给几个人？

 预设：生1：4个；  生2：40个

②全班笔算验证，生上黑板扮演。

 为什么要在被除数后面添0？追问：刚刚口算得到4的同学，你们猜猜他们是怎么算的？那你们的意思是扩大相同的倍数，那同时扩大10倍，可以吗？

   ③第二次比较：指着图6和图8，这两题，有什么不同？

   ④小结：当除数转化为整数的时候，我们发现被除数位数不够时，要在被除数的末尾用0补足。

    2.尝试除数小数位数小于被除数小数位数的竖式

    ①练习0.544÷0.16 

    ②反馈预设

你认为谁是对的？追问：看来你们一致认为被除数和除数要扩大相同倍数，后两个竖式商都一样，什么不一样？

    ③哪种看起来更简洁？追问 0.544544÷0.16 你会选择上面的哪种方法来转化？

    ④小结：看来在计算时，当被除数和除数的小数位数不同时，我们只要把除数转化成整数，被除数也跟着扩大到相同的倍数。

    【设计意图：当教学被除数和除数的小数位数不同时，适度放手，让学生基于学习经验，直接运用商不变规律，自主去尝试。通过学生暴露错误、师生交流、教师点拨等方式，帮助学生进一步巩固算理、修正错误、突破难点、掌握算法，理解当被除数、除数的小数位数不同时，以除数为标准转化为除数是整数的除法。】

   (五)梳理过程，归纳竖式算法

    1.回顾一下今天除数是小数的除法，我们是怎么计算的？

    2.小结：我们今天学了除数是小数的除法，根据商不变性质(板书)，转化成除数是整数的除法。我们要做到：

    一看：看除数有几位小数。

    二移：除数的小数点向右移动几位，被除数的小数点也要向右移动几位(位数不够的，在被除数的末尾用0补足)。

    三算：按除数是整数的小数除法进行计算

   用好这三步，我们就可以轻松计算除数是小数的除法。

   【设计意图：引导学生自主梳理算法，理清计算程序。“一看、二移、三算”六字快速帮助学生形成计算技能。适时渗透“转化”思想，为后续学生做好思想方法的铺垫。】          

三、巩固练习，感悟思想

1.第一关，比一比看谁算的又对又快，如图11。

 2 .第二关，解决问题。

    我有50元，准备去买水果，出示价格表，如图12。我想买一种水果，正好花完。你们说什么购买方案呢？那买两种水果呢，可以怎么买？

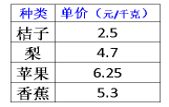
预设：生1：桔子可以，直接口算；生2：苹果也可以，笔算；生3：梨和香蕉不行，除不尽。

小结：你们能观察数据，根据数据的特点，通过不同的方法去解决，有口算、笔算、估算，真的很有策略。

   【设计意图：练习设计遵循“少而精，由易到难，循序渐进”的原则。利用口算题，强化商不变规律，熟练移动小数点的技能。解决问题让学生体验方法策略多样样，根据数据的特点，可以用不同的方法解决。】

四、课堂小结，点明转化

这节课，我们学了除数是小数的除法。我们要先转化除数是整数的除法。新知识转化成旧知识，常常是解决数学问题的有效方法，今后的数学学习中，我们还会经常用到。

   【设计意图：“立足当下，放眼未来”，再次渗透“转化”思想，为学生今后学习平面图形面积公式、立体图形体积公式、异分母分数加减法等新知识奠定思想方法基础，提升数学活动经验。】       

5.板书设计

6.教学反思

 除数是小数的除法，是一节计算课，算理的理解、竖式的写法都是学生第一次接触。本节课如果按照教材的顺序教学，学生就会学得很枯燥，教师也会很疲惫，算理的理解不会很透彻，计算也不会扎实。要避免这些弊端，就要合理地设计教学，发挥学生的主体作用。结合我自己在准备这节公开课的过程中的实践经验，我有以下三点想法。

    一、抓住转化的数学思想，让学生知其然并知其所以然。

 通过发红包的情境，再结合图形几何直观，让孩子去理解人民币之间的转化以及商不变性质。这样做不仅激发孩子的学习兴趣和欲望，还有利于理解它的算理。使学生体会了除数的小数的除法转化成除数是整数的除法就是把被除数和除数都同时换成相同度量单位去计算。学生在理解了算理的基础上就更深入理解了商不变的规律，进而理解了为什么要转化、怎样转化的问题。“转化”的数学思想贯穿始终。从开始的5.4÷0.3的研究到6.4÷0.16的研究，再到0.544÷0.16的研究，学生通过尝试、交流，亲历了转化的过程，意识到转化是一个非常重要的学习数学的方法。

    二、发挥学生的主体作用，在自主学习中建构认知结构。

每个学生都有自己独特的认知基础和思维方式，在新知建构和解决问题的过程总会有不同的呈现。让学生口算5.4÷0.3，并让说明为什么等于18。有人会利用单位换算，把元变为角，小数除法自然地转化成整数除法，使问题解决；有人会想到商不变规律去解决问题；有人会借助小数的意义去考虑。通过交流，三种方法都有一个共同的地方，都是把5.4除以0.3，转化成54除以3。其实口算方法就是理解算理的过程，教给孩子一种方法，口算与笔算的结合更有利于算理的理解，打通之间的关系。

当教学被除数和除数的小数位数不同时，适度放手，让学生基于学习经验，直接运用商不变规律，自主去尝试。最后通过几次的比较来总结计算方法，在教学中给了学生充分的自主学习空间，让学生在尝试、观察、比较、思考中完成新知与旧知同化，更新知识结构，收到了较好的效果。

    三、精心预设学生的想法，让错误成为有效的教学资源。

    当教学0.544÷0.16，我预设了学生可能会出现的几种做法：1、0.544÷0.16=544÷16；2、0.544÷0.16=544÷160；3、0.544÷0.16=54.4÷16

针对这样的情况，我就设想能不能让学生抓住第一种错误的做法进行分析，思考：“转化成544÷16算出的结果会和0.544÷0.16的结果一样吗？”然后再让学生说别的想法。学生在审视错误的过程中强化商不变的规律，并自然地得出正确的转化方法，那2和3转化方法都对，哪种看起来更简洁？追问 0.544544÷0.16 你会选择上面的哪种方法来转化？在比较的过程中，学生自然后选择第3种方法去转化，这样就自然理解了除数是小数的除法的算理：要把除数是小数的除法转化成除数是整数的除法。

精彩的生成来源于精心的预设，但是再精心的预设也不可能考虑到学生出现的所有情况。不过，教师对于学生出现的错误进行预设，就能让错误成为有效的教学资源。

编辑：陈丽娜

审核：叶锐睿

关注我们

公众号ID：《小数连心》

您的关注是我们更新的动力