【转载】弧长法（Riks Method）的基本原理

最新推荐文章于 2024-05-01 16:41:46 发布
最新推荐文章于 2024-05-01 16:41:46 发布
阅读量2.3k 收藏 3
点赞数
文章标签： javascript java matlab ViewUI
原文链接：http://www.cnblogs.com/shoout/p/9734744.html
版权
弧长法是结构非线性分析中的稳定计算方法，用于跟踪屈曲路径。在ABAQUS和ANSYS等商业软件中广泛使用。文章解释了弧长法的迭代过程，通过控制荷载增量步来越过极值点，介绍了如何确定迭代路径和荷载因子。还提供了一个通用求解程序的概要，并通过算例展示了其正确性。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

原地址：http://blog.163.com/zpfzcjndx@126/blog/static/635456812013017115922938/

       弧长法（Riks method）是目前结构非线性分析中数值计算最稳定、计算效率最高且最可靠的迭代控制方法之一，它有效地分析结构非线性前后屈曲及屈曲路径跟踪使其享誉"结构界"。大多数商业有限元软件(如ABAQUS、ANSYS等)也都将其纳入计算模块，作为一名工科生，机械式地"Step by Step"点击这些商业软件对话框的时候需"知其然，知其所以然"，否则必将"Rubbish in，Rubbish out"。

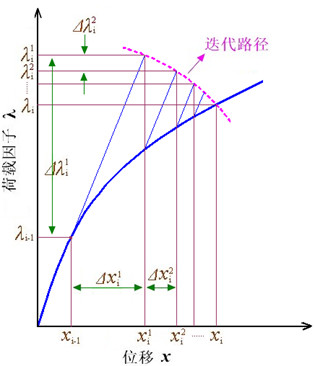
图1 弧长法迭代求解过程

图1 所示为弧长法的迭代求解过程，下标表示第个荷载步，上标表示第个荷载步下的第次迭代，显然，若荷载增量，则迭代路径为一条平行于轴的直线，即为著名的牛顿—拉夫逊法。

设第个荷载步收敛于，那么对于第个荷载步来说，需要进

最低0.47元/天 解锁文章
有限元分析-非线性求解技术(二)
YORU_NO_KUNI的博客
08-10 9008
本文主要对屈曲分析中涉及到的理论进行讲解，附带对ANSYS中的求解器进行说明。
非线性结构分析中的弧长法：原理、实现与应用
最新发布
01-09
内容概要：本文详细探讨了弧长法（Arc Length Method）及其在解决具有临界点的非线性有限元方程时的应用。内容分为三个部分：1) 基本理论介绍，包括边界值问题（BVP）的强形式和弱形式表述以及有限元近似方法；2) 数值解法对比，重点阐述了牛顿法在某些情况下失效的原因，并介绍了弧长法的工作原理、实现步骤以及优化选择；3) 应用实例展示，展示了从简单的桁架问题到复杂的多连通超弹性球膜系统膨胀模型的应用。这些应用案例不仅验证了弧长法的有效性和鲁棒性，还强调了它在解决复杂工程实际问题中的优势。 适合人群：对数值分析尤其是有限元方法有兴趣的研究人员及高年级学生，以及从事结构力学和连续介质力学领域的工程师和技术工作者。 使用场景及目标：①理解非线性结构行为（如snapping-through 和snapping-back），特别是在存在极限点的情况下；②提高数值仿真能力，确保即使当传统牛顿法无法继续跟踪路径时仍能得到可靠的解决方案。 阅读建议：本文涉及较深的专业知识，需要读者具备基本的固体物理与计算数学背景。对于想深入了解弧长法的人来说，推荐从具体应用例子出发，循序渐进地理解其背后的原理和技术细节。同时也可以参阅附录提供的程序代码链接以辅助学习。
结构非线性分析中的可控制方向的弧长法 (2001年)
04-26
对目前广泛应用于结构非线性分析中的弧长法进行了改进．改进后的弧长法在选择初始点后，可以从两个方向自动跟踪结构非线性平衡路径，该方法在结构非线性振动有限元分析中得到应用，数值算例表明了方法的有效性．
非线性有限元及结构力学模拟中的三类非线性问题
YIYIYYYYII的博客
08-06 3215
文章转自：公众号，有限元仿真分析 原文链接：https://mp.weixin.qq.com/s/9RXJ8f0nesvtrlsKx38Azg 线性分析 外加载荷与系统的响应之间为线性关系。例如线性弹簧，结构的柔度阵（将刚度阵集成并求逆）只需计算一次。通过将新的载荷向量乘以刚度阵的逆，可得到结构对其它载荷情况的线性响应。 此外，结构对各种载荷情况的响应，可以用常数放大和/或相互叠加，以确定它对一种全新载荷情况的响应，所提供的新载荷情况是前面各种载荷的叠加（或相乘）。这种载荷的叠加原理假定所有的载荷情况采
arcLength.rar_MATLAB 弧长法_arc length method_弧长_弧长法 有限元_有限元弧长法
07-14
有限元计算控制加载中弧长法（arc-length）的matlab源程序
弧长方法：使用弧长方法查找函数的根-matlab开发
05-29
任意函数或方程的根与与弧长二次控制方法相关的负载系数。 这种方法可以追踪平衡路径并提供适当的治疗极限点和分岔点。 对此，普通解决方案技术会导致极限点附近的不稳定，也有快速通过和快速返回的问题。 因此他们无法预测完整的载荷位移响应。 弧长法适用于原则上很好，在有限元中得到广泛接受分析，并已被广泛使用。 弧长法结构分析最初由 Riks (1972; 1979) 和Wempner (1971) 和后来被几位学者修改。 在这个包中，包括以下弧长控制方法： 1.克里斯菲尔德 (1981) 2.Lam & Morley (1992) 3.Ritto-Correa & Camotim (2008) 比其他两个更一般。 基本上，约束方程被添加到原始非线性中问题的控制方程，然后扩展系统方程通过增量迭代程序求解，例如牛顿-拉夫森（Newton-Raphson），改良的牛顿拉夫森（Newton Raphs
判断点在多边形内——弧长法
weixin_37946323的博客
07-08 1443
目录判断点在多边形内——弧长法计算弧长弧长计算由象限穿越代替代码 判断点在多边形内——弧长法 计算弧长 弧长法要求多边形是有向图，边左侧为多边形内域。 以被测点作单位圆，将多边形边镜像投影到单位圆，所谓单位圆的径向投影，其实就是多边形的有向边在被测点上转过的夹角[-pi,pi]，逆时针为正转角，顺时针为负转角。如果转角和为0，则点在多边形外；如果转角和为2*pi，则点在多边形内。 弧长计算由象限穿越代替 计算弧长比较费时间，所以用象限穿越代替计算弧长，如有向边自第Ⅰ象限穿越至第Ⅱ象限，则弧长+pi/2，反之
Arc-length.rar_ARC length_MATLAB 弧长法_arc-length_buckling_结构稳定
07-14
弧长法学习案例,用于学习结构屈曲稳定性的例子
ALmethod_弧长_弧长法MATLAB_ALmethod_弧长法
09-11
弧长法（Arc-Length Method）是一种在数值求解非线性方程组时常用的技术，其主要目的是控制迭代过程中的步长，防止解的不稳定性或发散。在MATLAB中实现弧长法，可以有效地解决一些具有强烈非线性的方程组。下面将...
牛顿拉夫逊法和弧长法的演示：牛顿拉夫逊法和拱长法-matlab开发
05-30
牛顿拉夫逊法和弧长法的演示
单次谐波非线性振动问题求解器：此 GUI 使用单次谐波表示法解决 MDOF 非线性振动问题。-matlab开发
06-01
GUI 是我在 METU 机械工程系为名为非线性振动的课程提交的项目工作。 此图形用户界面使用单次谐波表示计算在特定频率范围内具有非线性的多自由度系统的响应。 GUI 包含这些非线性：  立方刚度 分段线性刚度 干摩擦（滞后）  速度平方阻尼 分段线性粘性阻尼 间隙非线性 双线性粘性阻尼 双线性刚度GUI 使用单谐波描述函数来计算由频域中的非线性引起的力。 由于它只使用单次谐波来表示非线性，对于非奇对称的非线性，如间隙非线性、双线性刚度等，偏置项被忽略。如果可能，它有利于接收方法减少计算时间。 它使用弧长延拓法和牛顿法求解数值方程。 GUI 使用户能够改变受力并将非线性元素添加到线性系统。 所有参数均采用基本单位。 GUI 是在 MATLAB R2012a 中开发的。 该软件包包含一个简单的用户手册。
非线性方程组求解matlab程序_matlab非线性方程组弧长法,弧长法matlab
07-09
mulStablePoint 用不动点迭代法求非线性方程组的一个根 mulNewton 用牛顿法法求非线性方程组的一个根 mulDiscNewton 用离散牛顿法法求非线性方程组的一个根 mulMix 用牛顿-雅可比迭代法求非线性方程组的一个根 mulNewtonSOR 用牛顿-SOR迭代法求非线性方程组的一个根 mulDNewton 用牛顿下山法求非线性方程组的一个根 mulGXF1 用两点割线法的第一种形式求非线性方程组的一个根 mulGXF2 用两点割线法的第二种形式求非线性方程组的一个根 mulVNewton 用拟牛顿法求非线性方程组的一
有限元 弧长法 matlab,有没有有关弧长法的程序！！！
weixin_39989939的博客
03-17 903
% % % This is a code of Pseudo-Arc Length Continuation Method%the method can be used for solving the nonlinear equations%the principle can re found in some text booksclcclear% --------------------...
【编程实践】使用matlab求椭圆弧长
ZhiyangStudy的博客
03-14 1889
椭圆弧长计算。
MATLAB中用弧长法实现奇异方程，并且在图像中体现奇异点的性质。
weixin_52846855的博客
05-01 821
弧长法（Arc-length method）主要用于求解非线性方程和方程组，尤其是在需要追踪解路径，特别是当解可能遇到鞍点或拐点时。这个方法通过将非线性问题转化为等价的参数化问题来工作，参数即为弧长。请注意，弧长法的实现和性能可能会根据问题的具体细节而有所不同，这里提供的代码仅作为一个示例，可能需要针对特定问题进行调整。如果有相关问题欢迎留言咨询，或者关注VX公众号。对于奇异方程（即可能具有不同解的方程），弧长法特别有用，因为它允许方程在解的分岔点附近继续追踪路径。）是参数，L为[0,x]的取值。
曲线的弧长
jiongjiong 的专栏
12-12 2340
曲线的定义 原文： 来自维基百科： In general, a curve is defined through a continuous function γ:I→X\gamma: I\rightarrow X from an interval II of the real numbers into a topological space XX . Depending on the c
c#实现 改进弧长法判断点在多边形里面
cysisu的博客
11-16 837
一、开发环境：     VS2017，C# winform窗口程序 二、不同点      和网上的介绍不同，我也 不清楚是为什么，我去实现别的博客的思路，始终是在象限相差为2的地方会判断不正确，所以我自己思考了一种方法来进行这个地方的处理。 三、算法思路解释 1、为了介绍方便，先规定符号：    将需要判断的点叫做：centerPoint    多边形的顶点序列是：points[n]...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值