圆排列公式推导_应力分析基础篇--二向应力状态之应力圆

做设备的可能都知道四大强度理论，但是理解强度理论必须对材料的基本应力状态、应力分析有一定认识，小编今天分享一些这方面的知识。

应力圆就是一个很好的应力分析工具，通过应力圆可以直观的观察到应力状态，切应力和正应力的关系等。

四大强度理论

*薄壁圆筒简单分析*
以承受内压P的简单薄壁圆筒为例，圆筒壁厚δ远小于设备直径D，径向应力可以忽略不计，主要承受的应力为轴向应力和周向应力。建立等式可计算出周向应力为轴向应力的2倍。σθ=PD/2δ σψ=PD/4δ。

薄壁圆筒简单应力分析

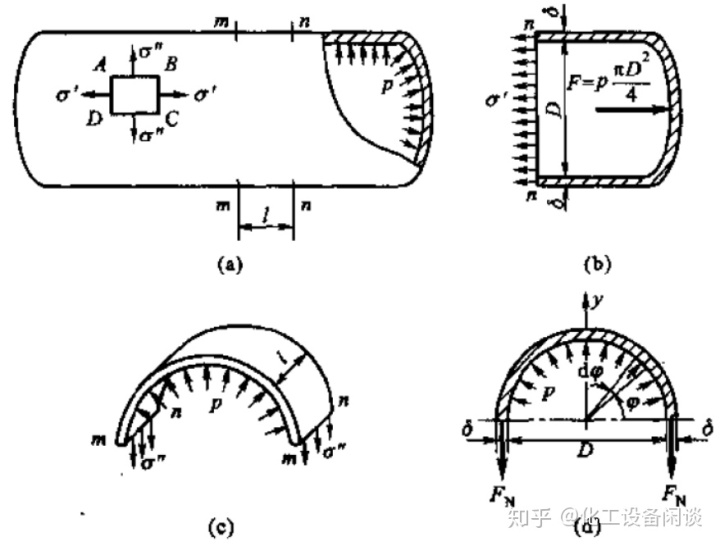
*单元体、主平面、主应力概念*

单元体：通过一点取正方形单元体，单元体尺寸无限小。此单元体的应力状态可以代表一点的应力状态。

单元体

正应力：单元体表面法向应力。

切应力：单元体表面切向应力。

主平面：上图单元体中表面切应力为零的平面称为主平面。

主应力：主平面上的正应力称为主应力。

*二向应力状态主平面推导*

在二向应力状态下，已知通过一点的某些截面上τxy，σx，σy后，计算通过这一点的其他截面上的应力，从而确定主应力和主平面。

计算简图

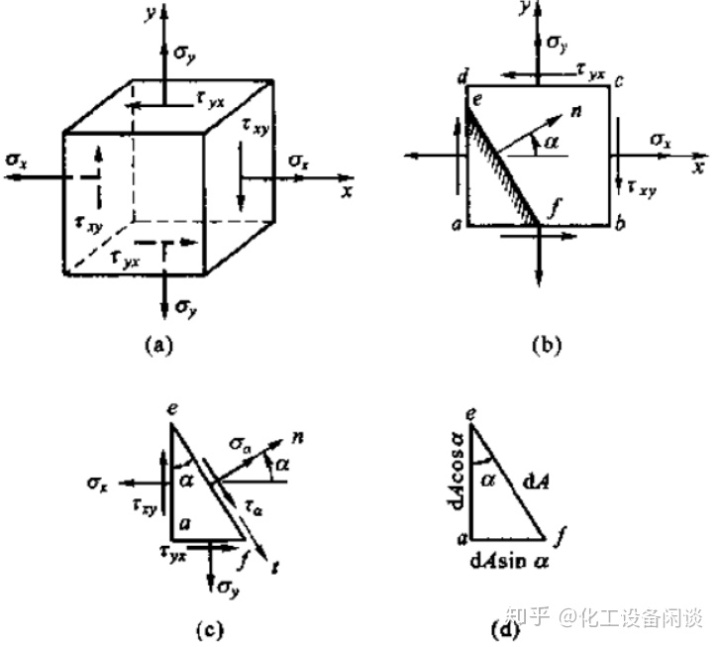
上图单元体承受二向应力状态，取任意斜截面ef，外法线n与X轴夹角为α。以图（c）为准，建立力的方程式。

具体推导过程小编就不叨叨叨了，感兴趣的可以翻翻力学教材。再考虑切应力互等定理，最后得出：

二向应力状态下，斜截面ef上的正应力和切应力

上述两式为关于α角的函数，可以对其求导，导数为0时，可求得最大或最小值。求导会发现，切应力为0的平面，正应力为最大或最小值（是真的，欢迎各位看官自己去算）。所以得出主平面上的主应力为最大或最小正应力。

如果不了解求导的知识，自行去翻高等数学的课本。工作了这么多年，小编越来越觉得数学有多重要，数学基础厉害，自己建立了模型，就可以求解。

*应力圆*

上述两公式等号两面平方相加可以得出：

应力圆公式

以横坐标表示σ，纵坐标表示τ，则圆心的横坐标为1/2（σx+σy），纵坐标为0，半径为上述等式等号右面的平方根。这个圆周称为应力圆。单元体内任意斜面的应力都对应着应力圆上的一个点。

应力圆

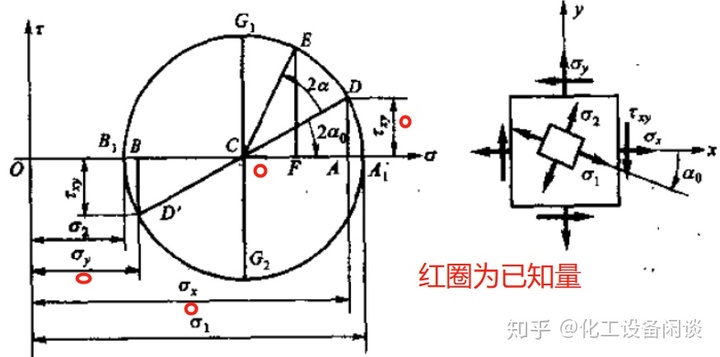
*应力圆的直观结论*

二向应力已知τxy，σx，σy后，就可以等比例绘制出应力圆。

（1）在图中可以得出最大正应力的值OA1，最小正应力OB1。

（2）可以测绘出各个斜截面应力值。

（3）可测绘得出主平面与已知力所在平面的夹角α0。

（4）G1为最大切应力所在点，A1为最大正应力所在点，夹角为90度，2α=90°，通过应力圆可以验证最大正应力和最大切应力夹角为45°。

（5）可更直观的理解为什么最大切应力为最大正应力和最小正应力差值的一半。

不当之处，欢迎批评指正！

了解更多应力分析知识，欢迎关注！