
一、可逆矩阵与逆矩阵
1.定义
对于矩阵A,如果存在一个矩阵B,使得
则称矩阵A为可逆矩阵,简称A可逆,称B为A的逆矩阵,记为
注意 矩阵A与B的地位是平等的,也可称B为可逆矩阵,
例如 设

则AB= BA= E,B为A的逆矩阵.
说明 若A是可逆矩阵,则A的逆矩阵是唯一的.
2.可逆矩阵的性质
性质1若矩阵A可逆,则A的逆矩阵唯一;
性质2若矩阵A可逆,则
性质3若矩阵A可逆,数
性质4若n阶矩阵A和B都可逆,则AB也可逆,且
推论 若
性质5若矩阵A可逆,则
性质6 若矩阵A可逆,则
说明 若矩阵A ,B ,C满足AB=AC,且A可逆,则
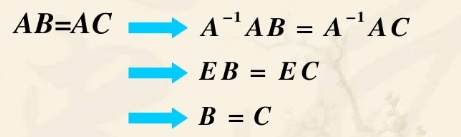
可逆矩阵相乘有消去律
二、可逆矩阵的判别
定义2 若方阵A满足
定义3设

中元素

称为矩阵A的转置伴随矩阵,习惯记为
由代数余子式组合定理

若

即

定理1 (逆矩阵的存在定理)
n阶矩阵A可逆的充分必要条件是


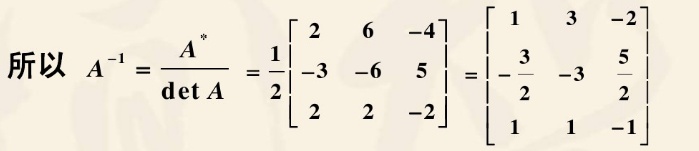









 本文介绍了可逆矩阵的概念,强调了可逆矩阵的逆矩阵是唯一的,并给出了多个关于可逆矩阵的性质,如乘法的消去律。此外,还阐述了非奇异矩阵作为可逆矩阵的判别条件,以及转置伴随矩阵在求逆过程中的作用。逆矩阵的存在定理指出,行列式不为零的方阵是可逆的。
本文介绍了可逆矩阵的概念,强调了可逆矩阵的逆矩阵是唯一的,并给出了多个关于可逆矩阵的性质,如乘法的消去律。此外,还阐述了非奇异矩阵作为可逆矩阵的判别条件,以及转置伴随矩阵在求逆过程中的作用。逆矩阵的存在定理指出,行列式不为零的方阵是可逆的。
















 1184
1184

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








