复数
(数的概念扩展
本词条由“科普中国”科学百科词条编写与应用工作项目 审核 。
我们把形如z=a+bi(a,b均为实数)的数称为复数，其中a称为实部，b称为虚部，i称为虚数单位。当z的虚部等于零时，常称z为实数；当z的虚部不等于零时，实部等于零时，常称z为纯虚数。复数域是实数域的代数闭包，即任何复系数多项式在复数域中总有根。复数是由意大利米兰学者卡当在十六世纪首次引入，经过达朗贝尔、棣莫弗、欧拉、高斯等人的工作，此概念逐渐为数学家所接受。
中文名
复数
外文名
complex number
表达式
z＝a+bi
提出者
Heron of Alexandria
提出时间
公元1世纪
适用领域
数学，编程
应用学科
数学，计算机
相关定理
欧拉公式、棣莫佛定理
所属集合
无序集
命名者
Rene Descartes
目录
1 历史
2 主要内容
▪ 定义
▪ 复数的模
3 共轭复数
▪ 释义
▪ 性质
4 复数的辐角
▪ 概述
▪ 释义
5 运算法则
6 分类
7 应用
▪ 系统分析
▪ 信号分析
▪ 反常积分
▪ 量子力学
▪ 相对论
▪ 应用数学
▪ 流体力学
▪ 碎形
▪ 实变初等函数
▪ 复变指数函数
▪ 复数的三角函数
历史
编辑
最早有关复数方根的文献出于公元1世纪希腊数学家海伦，他考虑的是平顶金字塔不可能问题。16世纪意大利米兰学者卡尔达诺(Jerome Cardan，1501—1576)在1545年发表的《重要的艺术》一书中，公布了一元三次方程的一般解法，被后人称之为“卡当公式”。他是第一个把负数的平方根写到公式中的数学家，并且在讨论是否可能把10分成两部分，使它们的乘积等于40时，他把答案写成
，尽管他认为和这两个表示式是没有意义的、想象的、虚无飘渺的，但他还是把10分成了两部分，并使它们的乘积等于40。给出“虚数”这一名称的是法国数学家笛卡尔(1596—1650)，他在《几何学》(1637年发表)中使“虚的数”与“实的数”相对应，从此，虚数才流传开来。
数系中发现一颗新星——虚数，于是引起了数学界的一片困惑，很多大数学家都不承认虚数。德国数学家莱布尼茨(1646—1716)在1702年说：“虚数是神灵遁迹的精微而奇异的隐避所，它大概是存在和虚妄两界中的两栖物”。然而，真理性的东西一定可以经得住时间和空间的考验，最终占有自己的一席之地。法国数学家达朗贝尔(1717—1783)在1747年指出，如果按照多项式的四则运算规则对虚数进行运算，那么它的结果总是a+bi的形式(a、b都是实数)。法国数学家棣莫弗(1667—1754)在1722年发现了著名的棣莫佛定理。欧拉在1748年发现了有名的关系式，并且是他在《微分公式》(1777年)一文中第一次用i来表示-1的平方根，首创了用符号i作为虚数的单位。“虚数”实际上不是想象出来的，而它是确实存在的。挪威的测量学家韦塞尔(1745—1818)在1797年试图给于这种虚数以直观的几何解释，并首先发表其作法，然而没有得到学术界的重视。
十八世纪末，复数渐渐被大多数人接受，当时卡斯帕尔·韦塞尔提出复数可看作平面上的一点。数年后，高斯再提出此观点并大力推广，复数的研究开始高速发展。诧异的是，早于1685年约翰·沃利斯已经在De Algebra tractatus提出此一观点。
卡斯帕尔·韦塞尔的文章发表在1799年的《Proceedings of the Copenhagen Academy》上，以当今标准来看，也是相当清楚和完备。他又考虑球体，得出四元数并以此提出完备的球面三角学理论。1804年，Abbé Buée亦独立地提出与沃利斯相似的观点，即以来表示平面上与实轴垂直的单位线段。1806年，Buée的文章正式刊出，同年让-罗贝尔·阿尔冈亦发表同类文章，而阿冈的复平面成了标准。1831年高斯认为复数不够普及，次年他发表了一篇备忘录，奠定复数在数学的地位。柯西及阿贝尔的努力，扫除了复数使用的最后顾忌，后者更是首位以复数研究著名的。
复数吸引了著名数学家的注意，包括库默尔(1844年)、克罗内克(1845年)、Scheffler(1845年、1851年、1880年)、Bellavitis(1835年、1852年)、乔治·皮库克(1845年)及德·摩根(1849年)。莫比乌斯发表了大量有关复数几何的短文，约翰·彼得·狄利克雷将很多实数概念，例如素数，推广至复数。
德国数学家阿甘得(1777—1855)在1806年公布了复数的图象表示法，即所有实数能用一条数轴表示，同样，复数也能用一个平面上的点来表示。在直角坐标系中，横轴上取对应实数a的点A，纵轴上取对应实数b的点B，并过这两点引平行于坐标轴的直线，它们的交点C就表示复数 。象这样，由各点都对应复数的平面叫做“复平面”，后来又称“阿甘得平面”。高斯在1831年，用实数组 代表复数 ，并建立了复数的某些运算，使得复数的某些运算也象实数一样地“代数化”。他又在1832年第一次提出了“复数”这个名词，还将表示平面上同一点的两种不同方法——直角坐标法和极坐标法加以综合。统一于表示同一复数的代数式和三角式两种形式中，并把数轴上的点与实数一一对应，扩展为平面上的点与复数一一对应。高斯不仅把复数看作平面上的点，而且还看作是一种向量，并利用复数与向量之间一一对应的关系，阐述了复数的几何加法与乘法。至此，复数理论才比较完整和系统地建立起来了。
经过许多数学家长期不懈的努力，深刻探讨并发展了复数理论，才使得在数学领域游荡了200年的幽灵——虚数揭去了神秘的面纱，显现出它的本来面目，原来虚数不“虚”。虚数成为了数系大家庭中一员，从而实数集才扩充到了复数集。
随着科学和技术的进步，复数理论已越来越显出它的重要性，它不但对于数学本身的发展有着极其重要的意义，而且为证明机翼上升力的基本定理起到了重要作用，并在解决堤坝渗水的问题中显示了它的威力，也为建立巨大水电站提供了重要的理论依据。
主要内容
编辑
定义
数集拓展到实数范围内，仍有些运算无法进行(比如对负数开偶数次方)，为了使方程有解，我们将数集再次扩充。
在实数域上定义二元有序对z=(a,b)，并规定有序对之间有运算"+"、"×" (记z1=(a,b),z2=(c,d))：
z1 + z2=(a+c,b+d)
z1 × z2=(ac-bd,bc+ad)
容易验证，这样定义的有序对全体在有序对的加法和乘法下成一个域，并且对任何复数z，我们有
z=(a,b)=(a,0)+(0,1) × (b,0)
令f是从实数域到复数域的映射，f(a)=(a,0)，则这个映射保持了实数域上的加法和乘法，因此实数域可以嵌入复数域中，可以视为复数域的子域。
记(0,1)=i,则根据我们定义的运算，(a,b)=(a,0)+(0,1) × (b,0)=a+bi，i × i=(0,1) × (0,1)=(-1,0)=-1，这就只通过实数解决了虚数单位i的存在问题。
形如
的数称为复数(complex number)，其中规定i为虚数单位，且
(a，b是任意实数)
我们将复数
中的实数a称为复数z的实部(real part)记作Rez=a
实数b称为复数z的虚部(imaginary part)记作 Imz=b.
当a=0且b≠0时，z=bi，我们就将其称为纯虚数。
复数的集合用C表示，实数的集合用R表示，显然，R是C的真子集。
复数集是无序集，不能建立大小顺序。
复数的模
将复数的实部与虚部的平方和的正的平方根的值称为该复数的模，记作∣z∣.
即对于复数
，它的模
共轭复数
编辑
释义
对于复数
，称复数
=a-bi为z的共轭复数。即两个实部相等，虚部互为相反数的复数互为共轭复数(conjugate complex number)。复数z的共轭复数记作
性质
根据定义，若
(a，b∈R)，则
=a－bi(a,b∈R)。共轭复数所对应的点关于实轴对称。两个复数：x+yi与x-yi称为共轭复数，它们的实部相等，虚部互为相反数。在复平面上，表示两个共轭复数的点关于X轴对称，而这一点正是"共轭"一词的来源----两头牛平行地拉一部犁，它们的肩膀上要共架一个横梁，这横梁就叫做"轭"。如果用z表示x+yi，那么在z字上面加个"一"就表示x-yi，或相反 [1] 。
共轭复数有些有趣的性质：
复数的辐角
编辑
概述
在复变函数中，自变量z可以写成
，r是z的模，即r = |z|；θ是z的辐角，记作：Arg(z)。在-π到π间的辐角称为辐角主值，记作：arg(z)(小写的A)。
释义
任意一个不为零的复数
的辐角有无限多个值，且这些值相差2π的整数倍。把适合于-π≤θ
指数形式：
。
运算法则
编辑
加法法则
复数的加法法则：设z1=a+bi，z2=c+di是任意两个复数。两者和的实部是原来两个复数实部的和，它的虚部是原来两个虚部的和。两个复数的和依然是复数。
即
乘法法则
复数的乘法法则：把两个复数相乘，类似两个多项式相乘，结果中i2= -1，把实部与虚部分别合并。两个复数的积仍然是一个复数。
即
除法法则
复数除法定义：满足
的复数
叫复数a+bi除以复数c+di的商。
运算方法：将分子和分母同时乘以分母的共轭复数，再用乘法法则运算，
即
开方法则
若
，则
(k=0，1，2，3…n-1)
运算律
加法交换律：z1+z2=z2+z1
乘法交换律：z1×z2=z2×z1
加法结合律：(z1+z2)+z3=z1+(z2+z3)
乘法结合律：(z1×z2)×z3=z1×(z2×z3)
分配律：z1×(z2+z3)=z1×z2+z1×z3
i的乘方法则
i4n+1=i, i4n+2=-1, i4n+3=-i, i4n=1(其中n∈Z)
棣莫佛定理
对于复数z=r(cosθ+isinθ)，有z的n次幂
zn=rn[cos(nθ)+isin(nθ)] (其中n是正整数)
则
分类
数的分类拓展到复数范围后，我们对复数范围的数集做以下分类
复数(a+bi)——集合符号C | ||||||
— | 实数(复数当b=0时)——集合符号R | |||||
— | — | 有理数——集合符号Q(p/q) | ||||
— | — | — | ①正有理数——集合符号Q+ | |||
— | — | — | — | 正整数——集合符号N+或N* | ||
— | — | — | — | — | 1 | |
— | — | — | — | — | 质数 | |
— | — | — | — | — | 合数 | |
— | — | — | — | 正分数 | ||
— | — | — | ①0 | |||
— | — | — | ①负有理数——集合符号Q- | |||
— | — | — | — | 负整数——集合符号Z- | ||
— | — | — | — | 负分数 | ||
— | — | — | ②整数——集合符号Z | |||
— | — | — | — | 奇数 | ||
— | — | — | — | 偶数 | ||
— | — | — | ②分数 | |||
— | — | 无理数 | ||||
— | — | — | 正无理数 | |||
— | — | — | 负无理数 | |||
— | 虚数(b≠0) | |||||
— | — | 纯虚数(a=0) | ||||
— | — | 混虚数(a≠0) | ||||
注：①②代表对“有理数”两种不同的分类方式。
应用
编辑
系统分析
在系统分析中，系统常常通过拉普拉斯变换从时域变换到频域。因此可在复平面上分析系统的极点和零点。分析系统稳定性的根轨迹法、奈奎斯特图法(Nyquist plot)和尼科尔斯图法(Nichols plot)都是在复平面上进行的。
无论系统极点和零点在左半平面还是右半平面，根轨迹法都很重要。如果系统极点
位于右半平面，则因果系统不稳定；都位于左半平面，则因果系统稳定；位于虚轴上，则系统为临界稳定的。如果系统的全部零点和极点都在左半平面，则这是个最小相位系统。如果系统的极点和零点关于虚轴对称，则这是全通系统。
信号分析
信号分析和其他领域使用复数可以方便的表示周期信号。模值|z|表示信号的幅度，辐角arg(z)表示给定频率的正弦波的相位。
利用傅立叶变换可将实信号表示成一系列周期函数的和。这些周期函数通常用形式如下的复函数的实部表示：
其中ω对应角频率，复数z包含了幅度和相位的信息。
电路分析中，引入电容、电感与频率有关的虚部可以方便的将电压、电流的关系用简单的线性方程表示并求解。(有时用字母j作为虚数单位，以免与电流符号i混淆。)
反常积分
在应用层面，复分析常用以计算某些实值的反常函数，藉由复值函数得出。方法有多种，见围道积分方法。
量子力学
量子力学中复数是十分重要的，因其理论是建基于复数域上无限维的希尔伯特空间。
相对论
如将时间变数视为虚数的话便可简化一些狭义和广义相对论中的时空度量 (Metric) 方程。
应用数学
实际应用中，求解给定差分方程模型的系统，通常首先找出线性差分方程对应的特征方程的所有复特征根r，再将系统以形为f(t) =e的基函数的线性组合表示。
流体力学
复函数于流体力学中可描述二维势流(2D Potential Flow)。
碎形
一些碎形如曼德勃罗集合和茹利亚集(Julia set) 是建基于复平面上的点的。
实变初等函数
我们把数学分析中基本的实变初等函数推广到复变初等函数，使得定义的各种复变初等函数，当z变为实变数x(y=0)时与相应的实变初等函数相同。
注意根据这些定义，在z为任意复变数时，
①．哪些相应的实变初等函数的性质被保留下来
②．哪些相应的实变初等函数的性质不再成立
③．出现了哪些相应的实变初等函数所没有的新的性质。
复变指数函数
ea+bi=eaebi=ea(cosb+isinb)
复数的三角函数
证明：把yi代入泰勒级数，借助
和
来化简即可；
同理可得aix=cos(xlna)+isin(xlna)= (eix)lna
借助eix=cosx+isinx可以方便地证明棣莫佛定理 [2] 。
向量
(数学用语)
编辑 讨论10 上传视频
本词条由“科普中国”科学百科词条编写与应用工作项目 审核 。
在数学中，向量(也称为欧几里得向量、几何向量、矢量)，指具有大小(magnitude)和方向的量。它可以形象化地表示为带箭头的线段。箭头所指：代表向量的方向；线段长度：代表向量的大小。与向量对应的量叫做数量(物理学中称标量)，数量(或标量)只有大小，没有方向。
向量的记法：印刷体记作黑体(粗体)的字母(如a、b、u、v)，书写时在字母顶上加一小箭头“→”。 [1] 如果给定向量的起点(A)和终点(B)，可将向量记作AB(并于顶上加→)。在空间直角坐标系中，也能把向量以数对形式表示，例如xOy平面中(2,3)是一向量。
在物理学和工程学中，几何向量更常被称为矢量。许多物理量都是矢量，比如一个物体的位移，球撞向墙而对其施加的力等等。与之相对的是标量，即只有大小而没有方向的量。一些与向量有关的定义亦与物理概念有密切的联系，例如向量势对应于物理中的势能。
几何向量的概念在线性代数中经由抽象化，得到更一般的向量概念。此处向量定义为向量空间的元素，要注意这些抽象意义上的向量不一定以数对表示，大小和方向的概念亦不一定适用。因此，平日阅读时需按照语境来区分文中所说的"向量"是哪一种概念。不过，依然可以找出一个向量空间的基来设置坐标系，也可以透过选取恰当的定义，在向量空间上介定范数和内积，这允许我们把抽象意义上的向量类比为具体的几何向量。
中文名
向量
外文名
vector
别 称
矢量
应用学科
物理，解析几何，计算机编程
适用领域范围
数学中的平面向量
适用领域范围
计算机赋值向量
目录
1 发展历史
2 表达方式
▪ 代数表示
▪ 几何表示
▪ 坐标表示
3 行列式的几何意义
4 相关定义
▪ 有向线段
▪ 向量的模
▪ 单位向量
▪ 负向量
▪ 零向量
▪ 相等向量
▪ 自由向量
▪ 滑动向量
▪ 固定向量
▪ 位置向量
▪ 方向向量
▪ 相反向量
▪ 平行向量
▪ 共面向量
▪ 法向量
▪ 向量的和的模
5 运算
▪ 加法
▪ 减法
▪ 数乘
▪ 数量积
▪ 向量积
▪ 三向量混合积
▪ 双重向量积
▪ 关系式
▪ 两个向量构成的平行四边形的面积公式
6 向量定理
▪ 共线定理
▪ 垂直定理
▪ 分解定理
▪ 定比分点公式
▪ 三点共线定理
▪ 重心判断式
▪ 垂心判断式
▪ 内心判断式
▪ 外心判断式
7 向量空间
▪ 定义
▪ 同构
▪ 映射
▪ 延伸
▪ 子空间及基
▪ 向量的中线公式
发展历史
编辑
向量，最初被应用于物理学。很多物理量如力、速度、位移以及电场强
向量
度、磁感应强度等都是向量。大约公元前350年前，古希腊著名学者亚里士多德就知道了力可以表示成向量，两个力的组合作用可用著名的平行四边形法则来得到。“向量”一词来自力学、解析几何中的有向线段。最先使用有向线段表示向量的是英国大科学家牛顿。
从数学发展史来看，历史上很长一段时间，空间的向量结构并未被数学家们所认识，直到19世纪末20世纪初，人们才把空间的性质与向量运算联系起来，使向量成为具有一套优良运算通性的数学体系。
向量能够进入数学并得到发展，首先应从复数的几何表示谈起。18世纪末期，挪威测量学家威塞尔首次利用坐标平面上的点来表示复数a+bi(a,b为有理数，且不同时等于0)，并利用具有几何意义的复数运算来定义向量的运算。把坐标平面上的点用向量表示出来，并把向量的几何表示用于研究几何问题与三角问题。人们逐步接受了复数，也学会了利用复数来表示和研究平面中的向量，向量就这样平静地进入了数学中。
但复数的利用是受限制的，因为它仅能用于表示平面，若有不在同一平面上的力作用于同一物体，则需要寻找所谓三维“复数”以及相应的运算体系。19世纪中期，英国数学家哈密尔顿发明了四元数(包括数量部分和向量部分)，以代表空间的向量。他的工作为向量代数和向量分析的建立奠定了基础．随后，电磁理论的发现者，英国的数学物理学家麦克斯韦把四元数的数量部分和向量部分分开处理，从而创造了大量的向量分析。
三维向量分析的开创，以及同四元数的正式分裂，是英国的居伯斯和海维塞德于19世纪80年代各自独立完成的。他们提出，一个向量不过是四元数的向量部分，但不独立于任何四元数。他们引进了两种类型的乘法，即数量积和向量积。并把向量代数推广到变向量的向量微积分．从此，向量的方法被引进到分析和解析几何中来，并逐步完善，成为了一套优良的数学工具。
表达方式
编辑
代数表示
一般印刷用黑体的小写英文字母(a、b、c等)来表示，手写用在a、b、c等字母上加一箭头(→)表示，如
，也可以用大写字母AB、CD上加一箭头(→)等表示。
几何表示
向量可以用有向线段来表示。有向线段的长度表示向量的大小，向量的大小，也就是向量的长度。长度为0的向量叫做零向量，记作长度等于1个单位的向量，叫做单位向量。
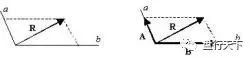向量表示
箭头所指的方向表示向量的方向。 [1]
坐标表示
在平面直角坐标系中，分别取与x轴、y轴方向相同的两个单位向量i，j作为一组基底。a为平面直角坐标系内的任意向量，以坐标原点O为起点P为终点作向量a。由平面向量基本定理可知，有且只有一对实数(x,y)，使得a=xi+yj，因此把实数对(x,y)叫做向量a的坐标，记作a=(x,y)。这就是向量a的坐标表示。其中(x,y)就是点
的坐标。向量a称为点P的位置向量。 [1]
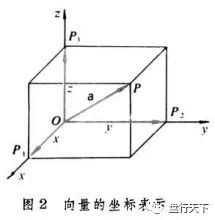向量的坐标表示
在空间直角坐标系中，分别取与x轴、y轴，z轴方向相同的3个单位向量i，j，k作为一组基底。若为该坐标系内的任意向量，以坐标原点O为起点作向量a。由空间基本定理知，有且只有一组实数(x,y,z)，使得a=ix+jy+kz，因此把实数对(x,y,z)叫做向量a的坐标，记作a=(x,y,z)。这就是向量a的坐标表示。其中(x,y,z)，就是点P的坐标。向量a称为点P的位置向量。
当然，对于多维的空间向量，可以通过类推得到，此略。
向量的矩阵表示
行列式的几何意义
编辑
行列式的值是一个数字，表示向量所在空间的【元素】 大小。
比如，在平面直角坐标系中，整个平面可以由长宽均为1的方格构成，这个方格的大小为1。这个方格就是平面直角坐标系中的【元素】，大小为1。
平面坐标系中所有的点都可以用
这两个向量来刻画，这两个向量也叫平面直角坐标空间的【标度】。
这两向量构成的行列式
那么，平面直角坐标系单元格大小，也就是【元素】大小为1的正方块。
再比如，我们对平面直角坐标系拉伸，用如下两个向量来刻画
那么，这个新坐标系(2维空间)的【元素】大小为2的长方块。
再比如，我们对平面直角坐标系变形，用如下两个向量来刻画
那么，这个新坐标系(2维空间)的【元素】大小为2的平行四边形块。
从以上3个例子，可以看出来：在2维空间中，两个2维向量构成的的行列式的值，等同于两个向量组成的平行四边形面积大小。也就是说，在2维空间中，两个2维向量构成的的行列式的值，等同于两个2维向量的【叉积】。
进一步，看3维空间。
比如，在空间直角坐标系中，这个空间可以由长宽高均为1的正方体构成，这个正方体的大小为1。这个正方体就是空间直角坐标系(3维空间)中的【元素】，大小为1。
那么可以看出来：在3维空间中，三个3维向量构成的的行列式的值，等同于三个3维向量的【混合积】。
由此，扩展到n维空间。在n维空间中，n个n维向量构成的行列式的值，表示n维向量所在的n维空间的【元素】 大小。同时，这n个n维向量也叫n维空间的【标度】。
相关定义
编辑
有向线段
规定若线段
的端点为起点，
为终点，则线段就具有了从起点
到终点
的方向和长度。
具有方向和长度的线段叫做有向线段。 [1]
向量的模
向量的大小，也就是向量的长度(或称模)。向量a的模记作|a|。 [1]
注：
1．向量的模是非负实数，向量的模是可以比较大小的。向量
，
。 [1]
2．因为方向不能比较大小，所以向量也就不能比较大小。对于向量来说“大于”和“小于”的概念是没有意义的。例如
是没有意义的。
单位向量
长度为一个单位(即模为1)的向量，叫做单位向量。与a同向，且长度为单位1的向量，叫做a方向上的单位向量，记作
。 [1]
负向量
如果向量AB与向量CD的模相等且方向相反，那么我们把向量AB叫做向量CD的负向量，也称为相反向量。 [1]
零向量
长度为0的向量叫做零向量，记作0。零向量的始点和终点重合，所以零向量没有确定的方向，或说零向量的方向是任意的。 [1]
相等向量
长度相等且方向相同的向量叫做相等向量．向量a与b相等，记作a=b。
规定：所有的零向量都相等。 [1]
当用有向线段表示向量时，起点可以任意选取。任意两个相等的非零向量，都可用同一条有向线段来表示，并且与有向线段的起点无关．同向且等长的有向线段都表示相同向量。
自由向量
始点不固定的向量，它可以任意的平行移动，而且移动后
向量
的向量仍然代表原来的向量。
在自由向量的意义下，相等的向量都看作是同一个向量。
数学中只研究自由向量。
滑动向量
沿着直线作用的向量称为滑动向量。
固定向量
作用于一点的向量称为固定向量(亦称胶着向量)。
位置向量
对于坐标平面内的任意一点P，我们把向量OP叫做点P的位置向量，记作：向量P。
方向向量
直线l上的向量a以及与向量a共线的向量叫做直线l上的方向向量。
相反向量
与a长度相等、方向相反的向量叫做a的相反向量，记作-a，有 -(-a)=a，零向量的相反向量仍是零向量。 [1]
平行向量
方向相同或相反的非零向量叫做平行(或共线)向量．向量a、b平行(共线)，记作a∥b。零向量长度为零，是起点与终点重合的向量，其方向不确定。我们规定：零向量与任一向量平行。平行于同一直线的一组向量是共线向量。 [1]
若a=(x,y)，b=(m,n)，则a//b→a×b=xn-ym=0
共面向量
平行于同一平面的三个(或多于三个)向量叫做共面向量。
空间中的向量有且只有以下两种位置关系：⑴共面；⑵不共面。
注意：只有三个或三个以上向量才谈共面不共面。
法向量
直线l⊥α，取直线l的方向向量a，则向量a叫做
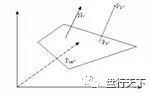法向量
平面α的法向量。 [2]
向量的和的模
设平面直角坐标系xOy中，有点A(x1,y1)、B(x2,y2)，则
运算
编辑
设
，
。
加法
向量的加法满足平行四边形法则和三角形法则，
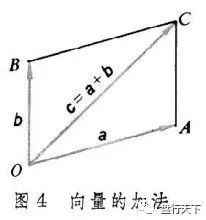向量的加法
。
向量加法的运算律：
交换律：a+b=b+a；
结合律：(a+b)+c=a+(b+c)。
减法
如果a、b是互为相反的向量，那么a=-b，b=-a，a+b=0. 0的反向量为0
OA-OB=BA.即“共同起点，指向被
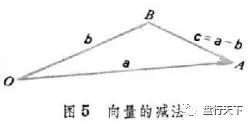向量的减法
减”
a=(x1,y1)，b=(x2,y2) ，则a-b=(x1-x2,y1-y2).
如图：c=a-b 以b的结束为起点，a的结束为终点。
加减变换律：a+(-b)=a-b
数乘
实数λ和向量a的叉乘乘积是一个向量，记作λa，且|λa|=|λ|*|a|。 [1]
当λ>0时，λa的方向与a的方向相同；当λ<0时，λa的方向与a的方向相反；当λ=0时，λa=0，方向任意。当a=0时，对于任意实数λ，都有λa=0。 [1]
注：按定义知，如果λa=0，那么λ=0或a=0。
实数λ叫做向量a的系数，乘数向量λa的几何意义就是将表示向量a的有向线段伸长或压缩。
当 |λ| >1时，表示向量a的有向线段在原方向(λ>0)或反方向(λ<0)上伸长为原来的|λ|倍
当|λ|<1时，表示向量a的有向线段在原方向(λ>0)或反方向(λ<0)上缩短为原来的 |λ|倍。
实数p和向量a的点乘乘积是一个数。
数与向量的乘法满足下面的运算律
结合律：(λa)·b=λ(a·b)=(a·λb)。
向量对于数的分配律(第一分配律)：(λ+μ)a=λa+μa.
数对于向量的分配律(第二分配律)：λ(a+b)=λa+λb.
数乘向量的消去律：① 如果实数λ≠0且λa=λb，那么a=b。② 如果a≠0且λa=μa，那么λ=μ。
需要注意的是：向量的加减乘(向量没有除法)运算满足实数加减乘运算法则。
数量积
定义：已知两个非零向量a,b，作OA=a,OB=b，则∠AOB称作向量a和向量b的夹角，记作θ并规定0≤θ≤π
定义：两个向量的数量积(内积、点积)是一个数量(没有方向)，记作a·b。
若a、b不共线，则
；若a、b共线，则
。 [1]
向量的数量积的坐标表示：a·b=x·x'+y·y'。
向量的数量积的运算律
a·b=b·a(交换律)
(λa)·b=λ(a·b)(关于数乘法的结合律)
(a+b)·c=a·c+b·c(分配律)
向量的数量积的性质
a·a=|a|的平方。
a⊥b〈=〉a·b=0。
|a·b|≤|a|·|b|。(该公式证明如下：|a·b|=|a|·|b|·|cosα| 因为0≤|cosα|≤1，所以|a·b|≤|a|·|b|)
向量的数量积与实数运算的主要不同点
1．向量的数量积不满足结合律，即：(a·b)·c≠a·(b·c)；例如：(a·b)²≠a²·b²。
2．向量的数量积不满足消去律，即：由a·b=a·c(a≠0)，推不出b=c。
3．|a·b|与|a|·|b|不等价
4．由 |a|=|b| ，不能推出a=b，也不能推出a=-b，但反过来则成立。
向量积
定义：两个向量a和b的向量积
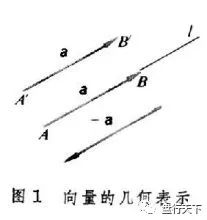向量的几何表示
(外积、叉积)是一个向量，记作a×b(这里“×”并不是乘号，只是一种表示方法，与“·”不同，也可记做“∧”)。若a、b不共线，则a×b的模是：∣a×b∣=|a|·|b|·sin〈a，b〉；a×b的方向是：垂直于a和b，且a、b和a×b按这个次序构成右手系。若a、b垂直，则∣a×b∣=|a|*|b|(此处与数量积不同，请注意)，若a×b=0，则a、b平行。向量积即两个不共线非零向量所在平面的一组法向量。
运算法则：运用三阶行列式
设a,b,c分别为沿x,y,z轴的单位向量
A=(x1,y1,z1)，B=(x2,y2,z2)，则
向量的向量积性质：
|a×b|是以a和b为边的平行四边形面积。
a×a=0。
a平行b〈=〉a×b=0
向量的向量积运算律
a×b=-b×a
(λa)×b=λ(a×b)=a×(λb)
a×(b+c)=a×b+a×c.
(a+b)×c=a×c+b×c.
上两个分配律分别称为左分配律和右分配律。在演算中应注意不能交换“×”号两侧向量的次序。
注：向量没有除法，“向量AB/向量CD”是没有意义的。
三向量混合积
定义：给定空间三向量a、b、c，向量a、b的向量积a×b，再和向量c作数量积(a×b)·c，
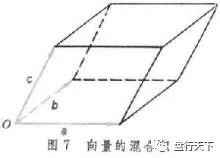向量的混合积
所得的数叫做三向量a、b、c的混合积，记作(a,b,c)或(abc)，即(abc)=(a,b,c)=(a×b)·c
混合积具有下列性质：
1．三个不共面向量a、b、c的混合积的绝对值等于以a、b、c为棱的平行六面体的体积V，并且当a、b、c构成右手系时混合积是正数；当a、b、c构成左手系时，混合积是负数，即(abc)=εV(当a、b、c构成右手系时ε=1；当a、b、c构成左手系时ε=-1)
2．上性质的推论：三向量a、b、c共面的充要条件是(abc)=0
3．(abc)=(bca)=(cab)=-(bac)=-(cba)=-(acb)
双重向量积
给定空间的三个向量a,b,c,如果先做其中两个向量a,b的向量积a×b，再做所得向量与第三向量的向量积，那么最后的结果仍然是一个向量，叫做所给三向量的双重向量积，记做：(a×b)×c。
性质：
(a×b)×c=(a·c)·b-(b·c)·a
a×(b×c)=-(b×c)×a=(a·c)·b-(a·b)·c
关系式
给定空间内四个向量a、b、c、d，则这四个向量之间满足如下关系：
证明：
由混合积的性质可知
(即把c×d看成一个新的向量e，利用性质(a×b)·e=a·(b×e))
再根据二重向量积的性质可知
该公式可用于证明三维的柯西不等式
证明：令公式中a=c、b=d，则：
设
，那么：
即
等号成立的条件是
，即a、b共线(
或b=0)
两个向量构成的平行四边形的面积公式
向量定理
编辑
共线定理
若b≠0，则a//b的充要条件是存在唯一实数λ，使
。若设a=(x1,y1)，b=(x2,y2) ，则有
，与平行概念相同。
平行于任何向量。
垂直定理
a⊥b的充要条件是a·b=0，即(x1x2+y1y2)=0 。
分解定理
平面向量分解定理：如果
、
是同一平面内的两个不平行向量，那么对于这一平面内的任一向量，有且只有一对实数
，使
，我们把不平行向量
、
叫做这一平面内所有向量的基底。
定比分点公式
叫做点P分有向线段
所成的比。
三点共线定理
已知O是AB所在直线外一点，若
,且
则A、B、C三点共线
重心判断式
在△ABC中，若
，则G为△ABC的重心。
垂心判断式
在△ABC中，若
，则H为△ABC的垂心。
内心判断式
在△ABC中，若
，且
，则I为△ABC的内心。
外心判断式
在△ABC中，若
，则O为△ABC的外心
此时O满足
。
向量空间
编辑
定义
给定域F，一个F上的向量空间是一个F-模。
同构
给定域F上的两个向量空间V与V' ，如果存在一个双射φ：V→V'，并且
，
，
。这样V与V' 便是同构的。
映射
给两个向量空间V和W在同一个F场，设定由V到W的线性变换或“线性映射” ，这些由V到W的映射都有共同点就是它们保持总和及标量商数。这个集合包含所有由V到W的线性映像，以 L(V,W) 来描述，也是一个F场里的向量空间。当V及W被确定后，线性映射可以用矩阵来表达。同构是一对一的一张线性映射。如果在V 和W之间存在同构， 我们称这两个空间为同构。一个在F场的向量空间加上线性映像就可以构成一个范畴，即阿贝尔范畴。
延伸
研究向量空间一般会涉及一些额外结构。额外结构如下：
一个实数或复数向量空间加上长度概念。就是范数称为赋范向量空间。
一个实数或复数向量空间加上长度和角度的概念，称为内积空间。
一个向量空间加上拓扑学符合运算的(加法及标量乘法是连续映射)称为拓扑向量空间。
一个向量空间加上双线性算子(定义为向量乘法)是个域代数。
子空间及基
一个向量空间V的一个非空子集合W在加法及标量乘法中表现密闭性，被称为V的线性子空间。给出一个向量集合B，那么包含它的最小子空间就称为它的扩张，记作span(B)。给出一个向量集合B，若它的扩张就是向量空间V， 则称B为V的生成集。一个向量空间V最大的线性独立子集，称为这个空间的基。若V=0，唯一的基是空集。对非零向量空间 V，基是 V 最小的生成集。如果一个向量空间 V 拥有一个元素个数有限的生成集，那么就称V是一个有限维空间。向量空间的所有基拥有相同基数，称为该空间的维度。例如，实数向量空间：
中，
的维度就是n。空间内的每个向量都有唯一的方法表达成基中元素的线性组合。把基中元素排列，向量便可以坐标系统来呈现。
向量的中线公式
若P为线段AB的中点，O为平面内一点，则
。
1813
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
