小学数学学过的几何图形有三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形,这些几何图形一般称为基本图形或规则图形,我们的面积及周长都有相应的公式直接计算。如下表:
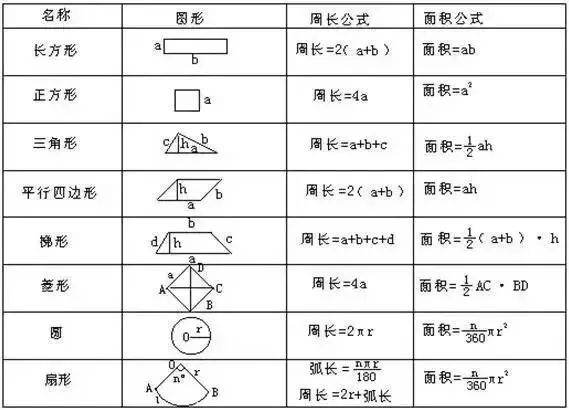
实际问题中,有些图形不是以基本图形的形状出现,而是由一些基本图形组合、拼凑成的,它们的面积及周长无法应用公式直接计算。一般我们称这样的图形为不规则图形。
那么,不规则图形的面积及周长怎样去计算呢?我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系,问题就能解决了。
常用的基本方法
1 相加法这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积。
例如:求下图整个图形的面积。
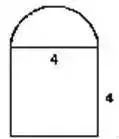 一句话:半圆的面积+正方形的面积=总面积
一句话:半圆的面积+正方形的面积=总面积
这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差。
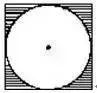
例如:下图,求阴影部分的面积。
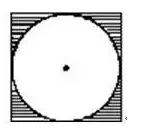
一句话:先求出正方形面积再减去里面圆的面积即可。
3 直接求法这种方法是根据已知条件,从整体出发直接求出不规则图形面积。
例如:下图,求阴影部分的面积。
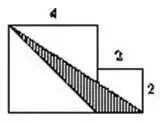
一句话:通过分析发现阴影部分就是一个底是2、高是4的三角形。
4 重新组合法这种方法是将不规则图形拆开,根据具体情况和计算上的需要,重新组合成一个新的图形,设法求出这个新图形面积即可。
例如:下图,求阴影部分的面积。
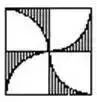
一句话:拆开图形,使阴影部分分布在正方形的4个角处,如下图。
这种方法是根据具体情况在图形中添一条或若干条辅助线,使不规则图形转化成若干个基本规则图形,然后再采用相加、相减法解决即可。
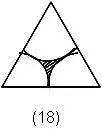
例如:下图,求两个正方形中阴影部分的面积。

一句话:此题虽然可以用相减法解决,但不如添加一条辅助线后用直接法作更简便(如下图)
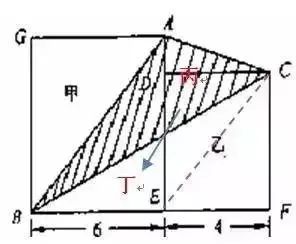
根据梯形两侧三角形面积相等原理(蝴蝶定理),可用三角形丁的面积替换丙的面积,组成一个大三角ABE,这样整个阴影部分面积恰是大正方形面积的一半。
6 割补法这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形,从而使问题得到解决。
例如:下图,若求阴影部分的面积。
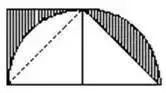
一句话:把右边弓形切割下来补在左边,这样整个阴影部分面积恰是正方形面积的一半。
7 平移法这种方法是将图形中某一部分切割下来平行移动到一恰当位置,使之组合成一个新的基本规则图形,便于求出面积。
例如:下图,求阴影部分的面积。
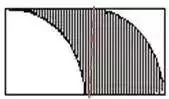
一句话:可先沿中间切开把左边正方形内的阴影部分平行移到右边正方形内,这样整个阴影部分恰是一个正方形。
8 旋转法这种方法是将图形中某一部分切割下来之后,使之沿某一点或某一轴旋转一定角度贴补在另一图形的一侧,从而组合成一个新的基本规则的图形,便于求出面积。
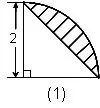
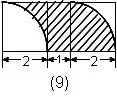
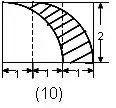
例如:下图(1),求阴影部分的面积。
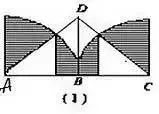
一句话:左半图形绕B点逆时针方向旋转180°,使A与C重合,从而构成右图(2)的样子,此时阴影部分的面积可以看成半圆面积减去中间等腰直角三角形的面积。
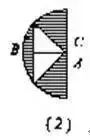
这种方法是作出原图形的对称图形,从而得到一个新的基本规则图形.原来图形面积就是这个新图形面积的一半。
例如:下图,求阴影部分的面积。
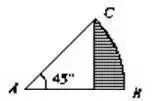
一句话:沿AB在原图下方作关于AB为对称轴的对称扇形ABD.弓形CBD的面积的一半就是所求阴影部分的面积。
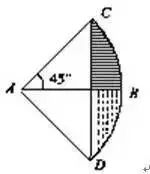
这种方法是将所求的图形看成是两个或两个以上图形的重叠部分。
例如:下图,求阴影部分的面积。
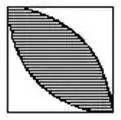
一句话:可先求两个扇形面积的和,减去正方形面积,因为阴影部分的面积恰好是两个扇形重叠的部分。
例题讲解:求阴影部分的面积
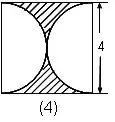
例1.求阴影部分的面积。(单位:厘米) 解:这是最基本的方法: | 例2.正方形面积是7平方厘米,求阴影部分的面积。(单位:厘米) 解:这也是一种最基本的方法用正方形的面积减去 |
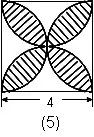
例3.求图中阴影部分的面积。(单位:厘米) 解:最基本的方法之一。用四个 | 例4.求阴影部分的面积。(单位:厘米)
解:同上,正方形面积减去圆面积,16-π( |
例5.求阴影部分的面积。(单位:厘米) 解:这是一个用最常用的方法解最常见的题,为方便起见, | 例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?
解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分) π |
例7.求阴影部分的面积。(单位:厘米) 解:正方形面积可用(对角线长×对角线长÷2,求) | 例8.求阴影部分的面积。(单位:厘米) 解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为 |
例9.求阴影部分的面积。(单位:厘米) 解:把右面的正方形平移至左边的正方形部分,则阴影部分合成一个长方形, | 例10.求阴影部分的面积。(单位:厘米)
解:同上,平移左右两部分至中间部分,则合成一个长方形, |
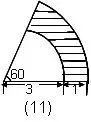
例11.求阴影部分的面积。(单位:厘米)
解:这种图形称为环形,可以用两个同心圆的面积差或差的一部分来求。 (π | 例12.求阴影部分的面积。(单位:厘米) 解:三个部分拼成一个半圆面积. |
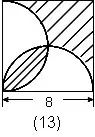
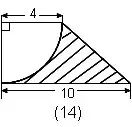
例13.求阴影部分的面积。(单位:厘米) 解: 连对角线后将"叶形"剪开移到右上面的空白部分,凑成正方形的一半. | 例14.求阴影部分的面积。(单位:厘米) 解:梯形面积减去 |
例15.已知直角三角形面积是12平方厘米,求阴影 部分的面积。
分析: 此题比上面的题有一定难度,这是"叶形"的一个半. | 例16.求阴影部分的面积。(单位:厘米) 解: |
例17.图中圆的半径为5厘米,求阴影部分的面积。(单位:厘米)
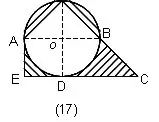
解:上面的阴影部分以AB为轴翻转后,整个阴影部分成为梯形减去直角三角形,或两个小直角三角形AED、BCD面积和。 | 例18.如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长。
解:阴影部分的周长为三个扇形弧,拼在一起为一个半圆弧, |
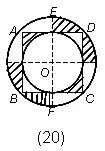
例19.正方形边长为2厘米,求阴影部分的面积。 解:右半部分上面部分逆时针,下面部分顺时针旋转到左半部分,组成一个矩形。 | 例20.如图,正方形ABCD的面积是36平方厘米,求阴影部分的面积。 解:设小圆半径为r,4 |
例21.图中四个圆的半径都是1厘米,求阴影部分的 面积。
解:把中间部分分成四等分,分别放在上面圆的四个角上,补成一个正方形,边长为2厘米, | 例22. 如图,正方形边长为8厘米,求阴影部分的面积。
解法一: 将左边上面一块移至右边上面,补上空白,则左边为一三角形,右边一个半圆. 阴影部分为一个三角形和一个半圆面积之和. π( |
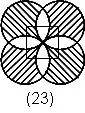
例23.图中的4个圆的圆心是正方形的4个顶点,,它们的公共点是该正方形的中心,如果每个圆的半径都是1厘米,那么阴影部分的面积是多少?
解:面积为4个圆减去8个叶形,叶形面积为: | 例24.如图,有8个半径为1厘米的小圆,用他们的圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心。如果圆周π率取3.1416,那么花瓣图形的的面积是多少平方厘米?
分析:连接角上四个小圆的圆心构成一个正方形,各个小圆被切去 解:阴影部分为大正方形面积与一个小圆面积之和. |
例25.如图,四个扇形的半径相等,求阴影部分的面积。(单位:厘米)
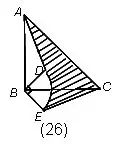
分析:四个空白部分可以拼成一个以2为半径的圆. | 例26.如图,等腰直角三角形ABC和四分之一圆DEB,AB=5厘米,BE=2厘米,求图中阴影部分的面积。 解: 将三角形CEB以B为圆心,逆时针转动90度,到三角形ABD位置,阴影部分成为三角形ACB面积减去 |
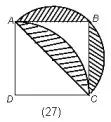
例27.如图,正方形ABCD的对角线AC=2厘米,扇形ACB是以AC为直径的半圆,扇形DAC是以D为圆心,AD为半径的圆的一部分,求阴影部分的面积。 解: 因为2 | 例28.求阴影部分的面积。(单位:厘米)
解法一:设AC中点为B,阴影面积为三角形ABD面积加弓形BD的面积, 三角形ABD的面积为:5×5÷2=12.5 弓形面积为:[π |
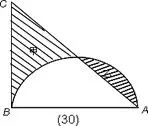
例29.图中直角三角形ABC的直角三角形的直角边AB=4厘米,BC=6厘米,扇形BCD所在圆是以B为圆心,半径为BC的圆,∠CBD= 解: 甲、乙两个部分同补上空白部分的三角形后合成一个扇形BCD,一个成为三角形ABC, | 例30.如图,三角形ABC是直角三角形,阴影部分甲比阴影部分乙面积大28平方厘米,AB=40厘米。求BC的长度。 解:两部分同补上空白部分后为直角三角形ABC,一个为半圆,设BC长为X,则 |
例31.如图是一个正方形和半圆所组成的图形,其中P为半圆周的中点,Q为正方形一边上的中点,求阴影部分的面积。 解:连PD、PC转换为两个三角形和两个弓形, | 例32.如图,大正方形的边长为6厘米,小正方形的边长为4厘米。求阴影部分的面积。 解:三角形DCE的面积为: |
例33.求阴影部分的面积。(单位:厘米) 解:用 | 例34.求阴影部分的面积。(单位:厘米) 解:两个弓形面积为:π |
例35.如图,三角形OAB是等腰三角形,OBC是扇形,OB=5厘米,求阴影部分的面积。 解:将两个同样的图形拼在一起成为 |
(免责声明:“快乐学习吧”旨在帮助更多的老师、家长和孩子,分享更多教育资讯,尊重原创并对原创者的文章表示肯定和感谢,相关文章均来自网络搜索,某些文章无法找到详细作者以明确出处请见谅。原作版权归原作者所有,如有侵权,请及时联系处理,我们将立即更正和删除相关内容。本公众号拥有对此声明的最终解







 这篇博客介绍了如何解决小学数学中正方形内两个扇形相交部分的阴影面积问题,讲解了不规则图形面积计算的6种常见方法,并通过例题详细阐述了解题步骤,帮助学生和家长理解并掌握这类问题的解决技巧。
这篇博客介绍了如何解决小学数学中正方形内两个扇形相交部分的阴影面积问题,讲解了不规则图形面积计算的6种常见方法,并通过例题详细阐述了解题步骤,帮助学生和家长理解并掌握这类问题的解决技巧。
 圆面积减去等腰直角三角形的面积,
圆面积减去等腰直角三角形的面积, 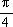 ×
×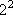 -2×1=1.14(平方厘米)
-2×1=1.14(平方厘米)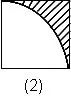
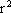 =7,
=7,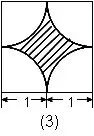

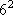 -π(
-π(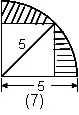
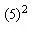 ÷4-12.5=7.125平方厘米 (注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)
÷4-12.5=7.125平方厘米 (注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形) 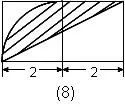
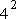 -π
-π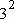 )×
)×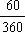 =
= ×3.14=3.66平方厘米
×3.14=3.66平方厘米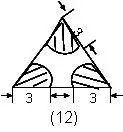
 (4+10)×4-
(4+10)×4-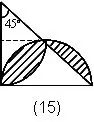
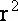 =12,
=12,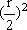 =6 圆面积为:π
=6 圆面积为:π =5.13平方厘米
=5.13平方厘米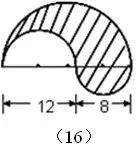
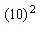 +π
+π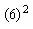 ]=
]=
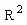 =2
=2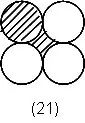
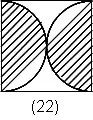

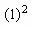 -1×1=
-1×1=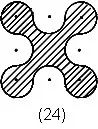
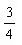 个圆,
个圆,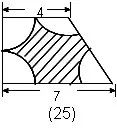
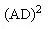 =
= =4,所以
=4,所以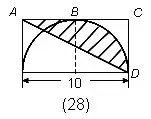
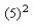 ÷2-5×5]÷2=7.125
÷2-5×5]÷2=7.125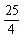 π
π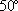 ,问:阴影部分甲比乙面积小多少?
,问:阴影部分甲比乙面积小多少?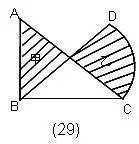
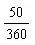 -
-
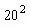 ÷2=28
÷2=28 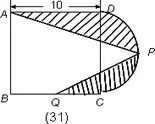
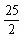 π-25=51.75平方厘米
π-25=51.75平方厘米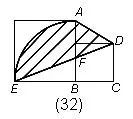
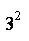 +π
+π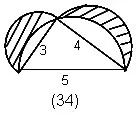
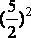 -3×4÷2=
-3×4÷2=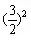 -(
-(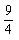 -
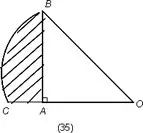
-
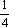 圆减等腰直角三角形[π
圆减等腰直角三角形[π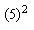 ÷4-
÷4- ×5×5]÷2=(
×5×5]÷2=(















 1874
1874

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








