随着信息技术和互联网的发展, 人们逐渐从信息匮乏的时代走入了信息过载的时代.如何快速而精准地从浩瀚的数据海洋中帮助用户获取感兴趣的信息, 已成为亟需解决的问题.推荐系统作为一种有效的信息过滤技术, 是解决这一问题的重要手段[.推荐系统通过收集和分析用户的历史行为来学习用户的喜好, 从而向用户推荐可能感兴趣的信息和服务.目前, 推荐系统已在很多领域得到了应用, 并为企业带来了可观的商业价值[.
在推荐系统领域, 矩阵分解模型因具有较好的理论基础[、良好的扩展性[和贝叶斯概率矩阵分解模型(Bayesian probabilistic matrix factorization, 简称BPMF)[, 使得矩阵分解模型可高效地处理大规模数据, 并取得较理想的推荐效果.在Netflix竞赛期间, Koren等人[在PMF的基础上, 综合用户的偏置、物品的偏置及用户的隐式反馈信息, 提出SVD++算法, 从而将矩阵分解模型在推荐系统中的应用推向了一个新的高度.
社交网络的普及, 为物品推荐应用中用户之间社会关系的获取提供了便利条件, 这种关系丰富了单个用户的信息, 从而能够更好地对用户建模.如何将用户之间的社会关系融入传统矩阵分解模型中, 是当前推荐系统研究的热点之一.研究者们[.
● 其一, 通过同时分解社会关系矩阵和评分矩阵并共享用户潜在特征矩阵的方式来对用户和物品进行建模[将用户的社会关系信息与评分信息相结合, 提出SoRec算法; Guo等人[将用户之间的信任关系强度融入PMF, 提出信任关系强度敏感的推荐算法StrengthMF;
● 其二, 将社会关系以正则化的方式来约束用户潜在特征矩阵的学习[使用用户的社会关系信息设计了社会正则化, 并将其用于约束PMF的目标函数, 提出SoReg算法; Jamali等人[将社交网络中的信任传播结构与PMF结合, 提出SocialMF算法, 该算法考虑了直接和间接信任的用户对目标用户评分的影响.
在物品推荐应用中, 除用户之间的社会关系外, 物品之间也存在一定的关联关系, 例如手机与手机配件之间的关联关系、衣服和鞋子之间的关联关系.物品之间的这种关联关系通常也会影响用户是否购买某一物品, 如何有效地获取物品之间的关联关系并将其应用到推荐系统中, 仍是当前研究的难点问题, 主要体现在:
(1) 物品之间关联关系是隐式的:用户之间的社会关系可通过社交网络直接获取, 而物品之间的关联关系却是隐式的, 无直接获取的途径;
(2) 物品之间的关联关系应是有向的:向购买手机的用户推荐手机配件成功的概率通常会比较高, 反向推荐则不一定成功.因此在获取物品之间关联关系时, 考虑有向性更为合理;
(3) 物品之间相关程度计算方法的合理性:在计算物品之间的相关程度时, 既要从微观的角度考虑两个物品个体之间的相关程度, 又要从全局角度分析两个物品相关程度的强弱;
(4) 如何将有向的关联关系融入到推荐模型中:在物品推荐过程中, 考虑的因素越多, 推荐模型越复杂, 求解空间越大, 因此需要一种有效的机制将关联关系融入到推荐模型中.
在已有的工作中:Sun等人[通过评分的时序信息来建立用户-物品的消费网络图, 并构建用户之间和物品之间的近邻关系, 然后将两者融入PMF中, 提出基于时序行为的协同过滤推荐算法; Wu等人[通过标签信息来构造用户和物品的相似性关系, 并将两者融入PMF中, 提出基于近邻的概率矩阵分解模型; Gu等人[通过使用物品的属性信息来获取物品的相似性关系, 并将其与社会关系相结合, 以图正则化的方式融入非负矩阵分解中, 提出基于图正则权重的非负矩阵分解模型; Liang等人[在解决推荐系统的物品排序任务时, 通过物品之间共现矩阵的点对互信息来计算物品之间的相关程度, 并与权重矩阵分解模型相结合, 提出联合分解模型CoFactor.这些工作通过不同的途径来获取物品之间的关联关系并将其应用到推荐领域中, 在一定程度上虽提高了传统推荐算法的性能, 但仍存在一定的问题.例如:文献[[、标签信息[、物品属性信息
针对物品之间关联关系获取这一难点问题, 本文在不借助外部信息的前提下, 综合物品之间的支持度与置信度, 提出一种从全局-局部角度计算物品之间相关程度的方法, 且由此所得关联关系是有向的.进一步, 综合考虑物品的关联关系、用户的社会关系, 将它们融入到传统矩阵分解模型中, 提出一种基于联合正则化的矩阵分解模型, 并给出相应的推荐算法CRMF(co-regularized matrix factorization).本文主要贡献有:
(1) 给出一种仅从用户-物品的交互矩阵中获取物品之间关联程度的计算方法, 它通过支持度与置信度, 分别从全局和局部角度来考虑物品之间的相关程度, 且由此所获取物品之间的关联关系具有有向性;
(2) 提出一种基于联合正则化的矩阵分解模型, 证明了联合正则化是一种加权原子范数, 理论上保证了该模型更加低秩, 从而使得在预测评分时采用较少的模型参数便可获得较为理想的推荐效果;
(3) 联合正则化矩阵分解模型因考虑自适应正则化, 使得构建的CRMF推荐算法应用于大规模非平衡数据集时更易搜索到合适的正则化超参数.
在4个真实数据集上的实验表明:CRMF与主流的推荐算法相比, 不仅可以缓解用户的冷启动问题, 而且能够更有效地预测不同类型用户的实际评分.
1 相关知识
在本文中, 我们使用Euclid Math One字体${\cal P}$表示集合, 大写字符P表示矩阵, Pij表示矩阵P的第i行第j列的值, Pi表示矩阵P的第i行向量, $\mathit{\boldsymbol{p}}_i^j$表示向量Pi的第j个值.本文使用的有关向量和矩阵的范数表示如下:
● $||{\mathit{\boldsymbol{p}}_i}|{|_2} = \sqrt {\sum\limits_{j = 1}^d {\mathit{\boldsymbol{p}}_i^j\mathit{\boldsymbol{p}}_i^j} } $, 称为向量的2范数;
● $||\mathit{\boldsymbol{P}}|{|_F} = \sqrt {\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^d {\mathit{\boldsymbol{P}}_{ij}^2} } } $, 称为矩阵的F范数.
此外, 我们使用PT表示矩阵的转置, tr(P)表示矩阵的迹, I=diag(I11, I22, …, Inn)表示一个对角矩阵, |${\cal P}$|表示集合${\cal P}$中的数量.
1.1 传统的矩阵分解
传统矩阵分解模型的基本思想m个用户和n个物品, 对于给定的评分矩阵R∈ $\mathbb{R}$m×n, 寻求两个潜在特征矩阵P和Q, 使得两者乘积近似拟合R. 使用随机梯度下降(stochastic gradient descent, 简称SGD)或交替最小二乘法(alternating least squares, 简称ALS), 可求出公式(1)的局部最优解P和Q:
$
f=\frac{1}{2}\sum\limits_{u=1}^{m}{\sum\limits_{j\in {{\mathcal{P}}_{u}}}{{{({{{\mathit{\boldsymbol{\hat{R}}}}}_{uj}}-{{\mathit{\boldsymbol{R}}}_{uj}})}^{2}}+\frac{\lambda }{2}(||\mathit{\boldsymbol{P}}||_{F}^{2}+||\mathit{\boldsymbol{Q}}||_{F}^{2})}}
$
(1)
其中, P∈$\mathbb{R}$m×d表示用户的潜在特征矩阵, Pu表示用户u的潜在特征向量, Q∈$\mathbb{R}$n×d表示物品的潜在特征矩阵, qj表示物品j的潜在特征向量, d≪min(m, n)表示特征向量维度.公式(1)中, Ruj > 0表示用户u对物品j的实际评分值, ${{\mathit{\boldsymbol{\hat{R}}}}_{uj}}=\mathit{\boldsymbol{p}}_{u}^{T}{{\mathit{\boldsymbol{q}}}_{j}}$表示用户u对物品j的预测评分值, ${\cal P}_u$表示用户u评分过的物品集合.超参数λ用于控制正则化的程度.传统的矩阵分解模型仅考虑了评分信息对用户和物品的潜在特征矩阵进行估计, 而忽略了与用户密切相关的社会关系信息, 有效地结合这些信息可提高推荐的精度.
1.2 社会正则化的矩阵分解
在社交网络中, 社会相关性理论指出, 人们比较喜欢与自己兴趣相投的用户建立连接, 因此, 目标用户决策时容易受到信任用户的影响, 且用户之间的信任度越高, 受影响程度越大.Ma等人[认为, 社会关系是用户之间兴趣相似的先验知识, 并提出用于约束传统矩阵分解目标函数的社会正则化, 如公式(2)所示:
$
\frac{1}{2}\sum\limits_{u=1}^{m}{\sum\limits_{v\in \mathcal{S}_{u}^{+}}{{{\mathit{\boldsymbol{S}}}_{uv}}||{{\mathit{\boldsymbol{p}}}_{u}}-{{\mathit{\boldsymbol{p}}}_{v}}||_{2}^{2}}}=tr[{{\mathit{\boldsymbol{P}}}^{T}}({{\mathit{\boldsymbol{D}}}^{p}}-\mathit{\boldsymbol{S}})\mathit{\boldsymbol{P}}]=tr({{\mathit{\boldsymbol{P}}}^{T}}{{\mathit{\boldsymbol{L}}}^{p}}\mathit{\boldsymbol{P}})
$
(2)
其中,
● S表示社会关系矩阵;
● Suv表示用户u与用户v的相似度, 由公式(3)计算得到:
$
{{\mathit{\boldsymbol{S}}}_{uv}}=\frac{\sum\limits_{j\in ({{\mathcal{P}}_{u}}\cap {{\mathcal{P}}_{v}})}{({{\mathit{\boldsymbol{R}}}_{uj}}-{{{\mathit{\boldsymbol{\bar{R}}}}}_{u}})({{\mathit{\boldsymbol{R}}}_{vj}}-{{{\mathit{\boldsymbol{\bar{R}}}}}_{v}})}}{\sqrt{\sum\limits_{j\in ({{\mathcal{P}}_{u}}\cap {{\mathcal{P}}_{v}})}{{{({{\mathit{\boldsymbol{R}}}_{uj}}-{{{\mathit{\boldsymbol{\bar{R}}}}}_{u}})}^{2}}}}\sqrt{{{\sum\limits_{j\in ({{\mathcal{P}}_{u}}\cap {{\mathcal{P}}_{v}})}{({{\mathit{\boldsymbol{R}}}_{vj}}-{{{\mathit{\boldsymbol{\bar{R}}}}}_{v}})}}^{2}}}}
$
(3)
● $\mathcal{S}_u^ + $表示用户u拥有的社会关系集合;
● 矩阵Dp是与用户相关的对角矩阵, 且$\mathit{\boldsymbol{D}}_{uu}^p = \sum\nolimits_{v = 1}^m {{\mathit{\boldsymbol{S}}_{uv}}} $;
● 矩阵Lp=Dp-S是与用户相关的拉普拉斯矩阵;
● ${\cal P}_u$, ${\cal P}_v$分别表示训练集中用户u, v的评分集合;
● ${{\mathit{\boldsymbol{\bar{R}}}}_{u}},{{\mathit{\boldsymbol{\bar{R}}}}_{v}}$分别表示训练集中用户u, v的平均评分.
公式(2)与公式(1)结合, 可得社会正则化的矩阵分解模型的目标函数, 如公式(4)所示:
$f=\frac{1}{2}\sum\limits_{u=1}^{m}{\sum\limits_{j\in {{\mathcal{P}}_{u}}}{{{({{{\mathit{\boldsymbol{\hat{R}}}}}_{uj}}-{{\mathit{\boldsymbol{R}}}_{uj}})}^{2}}}}+\frac{\lambda }{2}(||\mathit{\boldsymbol{P}}||_{F}^{2}+||\mathit{\boldsymbol{Q}}||_{F}^{2})+\frac{\beta }{2}tr({{\mathit{\boldsymbol{P}}}^{T}}{{\mathit{\boldsymbol{L}}}^{p}}\mathit{\boldsymbol{P}})
$
(4)
其中, β控制着社会关系在用户决策时所占的比重.上述目标函数通过社会正则化的方式约束用户潜在特征向量的学习, 使得当目标用户为冷启动用户时, 其潜在特征向量更多地表现为社交网络中近邻用户的特征因子.但该模型潜在假设物品之间是相互独立的, 忽略了现实世界中物品之间普遍存在着关联关系的事实.
2 联合正则化的矩阵分解
2.1 物品之间关联关系的获取
物品之间的关联关系在推荐应用中是影响用户决策的重要因素之一, 如何从用户-物品之间的交互矩阵中有效地量化物品之间的关联程度并获取它们之间有向的关联关系, 是推荐过程中核心步骤之一.文献[Support)与置信度(Confidence)可在一定程度上反映物品j与物品i之间的相关程度, 计算方法分别如公式(5)和公式(6)所示:
$
Support\left( j,i \right)=|{{\mathcal{Q}}_{i}}\cap {{\mathcal{Q}}_{j}}\left| / \right|{{\mathcal{R}}^{tr}}|
$
(5)
$
Confidence(j\to i)=|{{\mathcal{Q}}_{i}}\cap {{\mathcal{Q}}_{j}}\left| / \right|{{\mathcal{Q}}_{j}}|
$
(6)
其中, |$\mathcal{R}^{tr}$|表示在用户-物品交互矩阵中对物品做过评价的总人次数, 即评分矩阵R中非零元素个数; $\mathcal{Q}_i$, $\mathcal{Q}_j$分别表示对物品i和j做过评价的用户集合.从公式(5)可得出, 支持度从全局的角度反映了物品之间的相关程度, 由此获得的关联关系是无向的; 从公式(6)可得出, 置信度则从局部的两个物品来计算物品之间的相关程度, 由此获得的关联关系是有向的.如果单独考虑两者中的任意一个作为物品之间相关程度度量方法, 则无法兼顾物品间关联关系的有向性及全局-局部特性.此外, 若以数据挖掘中的关联规则来获取物品之间的关联关系, 通常需要支持度和置信度大于相应的阈值时才有效[.然而在推荐应用中, 支持度阈值和置信度阈值往往不易选取, 过高的阈值将会减少关联关系的数量, 过低的阈值会导致考虑较多的关联关系, 使得模型训练需要较多的时间.
为解决上述获取物品之间关联关系的不足之处, 在综合考虑物品之间支持度与置信度的基础之上, 本文定义了物品之间关联程度的计算方法, 如公式(7)所示:
$
{{\mathit{\boldsymbol{W}}}_{ji}}=\frac{Support(j,i)}{Support(j,i)+\varphi }\times Confidence(j\to i)=\frac{|{{\mathcal{Q}}_{i}}\cap {{\mathcal{Q}}_{j}}|}{|{{\mathcal{Q}}_{i}}\cap {{\mathcal{Q}}_{j}}|+\rho }\times \frac{|{{\mathcal{Q}}_{i}}\cap {{\mathcal{Q}}_{j}}|}{|{{\mathcal{Q}}_{j}}|}
$
(7)
其中, W表示物品之间的关联关系矩阵, Wji表示物品j与物品i之间的关联程度, ϕ≥0是一个适用于所有物品的超参数, ρ=ϕ|$\mathcal{R}^{tr}$|.在公式(7)中, 第2项Confidence(j→i)从局部的角度考虑了两个物品个体之间的相关程度, 第1项融合Support(j, i), 用于从全局角度调节两个物品之间的相关程度.当超参数ϕ=0(即ρ=0)时, Wji= Confidence(j→i), 此时, 两个物品之间的关联程度等于关联规则中的置信度.当超参数ϕ为大于0的固定值时, 若反映物品j与物品i之间全局相关程度的Support(j, i)越大, 则第1项的值也越大; 若Support(j, i)的值很小, 即便物品j到物品i的Confidence(j→i)比较高, 则也可通过第1项相应地降低它们之间的关联程度Wji的值.
由公式(7)可知:在不借助外部信息的前提下, 仅从用户-物品之间的交互矩阵中便可获取物品之间的关联关系.由于Confidence(i→j)≠Confidence(j→i), 则Wij≠Wji, 因此, 本文所定义的公式(7)可在一定程度上反映物品之间关联关系的有向性.
在下文中, 使用$\mathcal{W}$表示物品之间的关联关系集合, $\mathcal{W}_j^ + $表示物品j相关联的物品集合.在选择物品j的关联关系时, 首先根据Wji对关联程度进行排序, 然后对目标物品j选择关联程度最大的σ个物品作为近邻集$\mathcal{W}_j^ + $, 进一步简化关联关系集合$\mathcal{W}$.
2.2 模型定义
获取到物品的关联关系之后, 我们可将其应用到已有的矩阵分解模型.此时, 物品的潜在特征向量将受到存在关联关系的物品的影响.与社会正则化相似, 由物品的关联关系可得出关联正则化, 如公式(8)所示:
$
\frac{1}{2}\sum\limits_{j=1}^{n}{\sum\limits_{i\in \mathcal{W}_{j}^{+}}{{{\mathit{\boldsymbol{W}}}_{ji}}||{{\mathit{\boldsymbol{q}}}_{j}}-{{\mathit{\boldsymbol{q}}}_{i}}||_{2}^{2}}}=tr[{{\mathit{\boldsymbol{Q}}}^{T}}({{\mathit{\boldsymbol{D}}}^{q}}-\mathit{\boldsymbol{W}})\mathit{\boldsymbol{Q}}]=tr({{\mathit{\boldsymbol{Q}}}^{T}}{{\mathit{\boldsymbol{L}}}^{q}}\mathit{\boldsymbol{Q}})
$
(8)
其中, 矩阵Dq是与物品相关的对角矩阵且$\mathit{\boldsymbol{D}}_{jj}^{q}=\sum\nolimits_{i=1}^{n}{{{\mathit{\boldsymbol{W}}}_{ji}}}$, 矩阵Lq=Dq-W是与物品相关的拉普拉斯矩阵.我们将关联正则化融入基于社会正则化的矩阵分解模型可得改进后的目标函数如公式(9)所示:
$
f=\frac{1}{2}\sum\limits_{u=1}^{m}{\sum\limits_{j\in {{\mathcal{P}}_{u}}}{{{({{{\mathit{\boldsymbol{\hat{R}}}}}_{uj}}-{{\mathit{\boldsymbol{R}}}_{uj}})}^{2}}}}+\frac{\lambda }{2}(||\mathit{\boldsymbol{P}}||_{F}^{2}+||\mathit{\boldsymbol{Q}}||_{F}^{2})+\frac{\beta }{2}tr({{\mathit{\boldsymbol{P}}}^{T}}{{\mathit{\boldsymbol{L}}}^{p}}\mathit{\boldsymbol{P}})+\frac{\alpha }{2}tr({{\mathit{\boldsymbol{Q}}}^{T}}{{\mathit{\boldsymbol{L}}}^{q}}\mathit{\boldsymbol{Q}})
$
(9)
其中, 超参数α > 0用于控制物品的关联关系在推荐过程中所占的比重.
上述目标函数在求解模型参数时, 用于避免过拟合的正则化对于每个用户(物品)使用相同的超参数, 使得学习与系统交互频繁的用户(物品)的潜在特征向量时可能出现欠拟合, 在学习与系统交互较少的用户(物品)的潜在特征向量时可能出现过拟合.Salakhutdinov等人[认为:在学习用户(物品)的潜在特征向量时, 根据用户(物品)的评分数量进行不同程度的惩罚会比较合理, 由此可知需考虑自适应正则化.由文献[
$
f=\overbrace{\frac{\lambda }{2}\left( \sum\limits_{u=1}^{m}{|{{\mathcal{P}}_{u}}{{|}^{-\frac{1}{2}}}||{{\mathit{\boldsymbol{p}}}_{u}}||_{2}^{2}}+\sum\limits_{j=1}^{n}{|{{\mathcal{Q}}_{u}}{{|}^{-\frac{1}{2}}}||{{\mathit{\boldsymbol{q}}}_{j}}||_{2}^{2}} \right)}^{自适应正则化}+\frac{1}{2}\sum\limits_{u=1}^{m}{\sum\limits_{j\in {{\mathcal{P}}_{u}}}{{{({{{\mathit{\boldsymbol{\hat{R}}}}}_{uj}}-{{\mathit{\boldsymbol{R}}}_{uj}})}^{2}}}}\\
+\frac{\beta }{2}tr({{\mathit{\boldsymbol{P}}}^{T}}{{\mathit{\boldsymbol{L}}}^{p}}\mathit{\boldsymbol{P}})+\frac{\alpha }{2}tr({{\mathit{\boldsymbol{Q}}}^{T}}{{\mathit{\boldsymbol{L}}}^{q}}\mathit{\boldsymbol{Q}}) \\
=\frac{1}{2}\sum\limits_{u=1}^{m}{\sum\limits_{j\in {{\mathcal{P}}_{u}}}{{{({{{\mathit{\boldsymbol{\hat{R}}}}}_{uj}}-{{\mathit{\boldsymbol{R}}}_{uj}})}^{2}}}}+\underbrace{\frac{1}{2}tr({{\mathit{\boldsymbol{P}}}^{T}}{{{\mathit{\boldsymbol{\tilde{L}}}}}^{p}}\mathit{\boldsymbol{P}})+\frac{1}{2}tr({{\mathit{\boldsymbol{Q}}}^{T}}{{{\mathit{\boldsymbol{\tilde{L}}}}}^{q}}\mathit{\boldsymbol{Q}})}_{联合正则化} \\
$
(10)
其中, $ {{{\mathit{\boldsymbol{\tilde{L}}}}}^{p}}=\lambda {{\mathit{\boldsymbol{I}}}^{p}}+\beta {{\mathit{\boldsymbol{L}}}^{p}},{{\mathit{\boldsymbol{I}}}^{p}}=diag\left( |{{\mathcal{P}}_{1}}{{|}^{-\frac{1}{2}}},...,|{{\mathcal{P}}_{u}}{{|}^{-\frac{1}{2}}},...,|{{\mathcal{P}}_{m}}{{|}^{-\frac{1}{2}}} \right),$${{\mathit{\boldsymbol{I}}}^{q}}=diag\left( |{{\mathcal{Q}}_{1}}{{|}^{-\frac{1}{2}}},...,|{{\mathcal{Q}}_{j}}{{|}^{-\frac{1}{2}}},...,|{{\mathcal{Q}}_{n}}{{|}^{-\frac{1}{2}}} \right),{{{\mathit{\boldsymbol{\tilde{L}}}}}^{q}}=\lambda {{\mathit{\boldsymbol{I}}}^{q}}+\alpha {{\mathit{\boldsymbol{L}}}^{q}}.$
为了说明联合正则化的有效性, 我们以下给出详细的理论分析.根据文献[${\mathcal{F}_*} = \{ {\mathit{\boldsymbol{x}}_i}z_i^T:||{\mathit{\boldsymbol{x}}_i}|{|_2} = ||{\mathit{\boldsymbol{z}}_i}|{|_2} = 1\} $的gauge函数, $\mathcal{F} ^*$中每个秩为1的矩阵都有单位F范数.假设U∈$\mathbb{R}$m×m是由一组基向量组成的矩阵, $\mathit{\boldsymbol{S}}_U^{ - 1/2}$是一个对角矩阵且${(\mathit{\boldsymbol{S}}_U^{ - 1/2})_{ii}} \geqslant 0$表示第i个基向量所占的权重.
同样可假设V∈$\mathbb{R}$n×n, ${(\mathit{\boldsymbol{S}}_V^{ - 1/2})_{ii}} \geqslant 0$.令$\mathit{\boldsymbol{A}} = \mathit{\boldsymbol{US}}_U^{ - 1/2},\mathit{\boldsymbol{B}} = \mathit{\boldsymbol{VS}}_V^{ - 1/2}$, 由此可得加权的原子集如公式(11)所示:
$
\mathcal{F}=\{{{a}_{i}}={{\mathit{\boldsymbol{p}}}_{i}}\mathit{\boldsymbol{q}}_{i}^{T}:{{\mathit{\boldsymbol{p}}}_{i}}=\mathit{\boldsymbol{A}}{{\mathit{\boldsymbol{x}}}_{i}},{{\mathit{\boldsymbol{q}}}_{i}}=\mathit{\boldsymbol{B}}{{\mathit{\boldsymbol{z}}}_{i}},||{{\mathit{\boldsymbol{x}}}_{i}}|{{|}_{2}}=||{{\mathit{\boldsymbol{z}}}_{i}}|{{|}_{2}}=1\}
$
(11)
其中, 加权原子集$\mathcal{F} $中每个原子a都有非单位F范数.基于加权的原子集, 可定义加权原子范数如公式(12)所示:
$
||\mathit{\boldsymbol{\hat{R}}}|{{|}_{\mathcal{F}}}=\inf \sum\nolimits_{{{a}_{i}}\in \mathcal{F}}{|{{c}_{i}}|},\ \ {\rm{ s}\rm{.t}\rm{. }}\ \ \mathit{\boldsymbol{\hat{R}}}=\sum\nolimits_{{{a}_{i}}\in \mathcal{F}}{{{c}_{i}}}{{a}_{i}}
$
(12)
定理1. 对于任意的$\mathit{\boldsymbol{A}} = \mathit{\boldsymbol{US}}_U^{ - 1/2},\mathit{\boldsymbol{B}} = \mathit{\boldsymbol{VS}}_V^{ - 1/2}$和加权的原子集$\mathcal{F} $, 可得出:
$
||\mathit{\boldsymbol{\hat{R}}}|{{|}_{\mathcal{F}}}=\underset{\mathit{\boldsymbol{P}},\mathit{\boldsymbol{Q}}}{\mathop{\rm{inf}}}\,\frac{1}{2}\{||{{\mathit{\boldsymbol{A}}}^{-1}}\mathit{\boldsymbol{P}}||_{F}^{2}+||{{\mathit{\boldsymbol{B}}}^{-1}}\mathit{\boldsymbol{Q}}||_{F}^{2}\},\ \ {\rm{ s}\rm{.t}\rm{. }}\ \ \mathit{\boldsymbol{\hat{R}}}=\mathit{\boldsymbol{P}}{{\mathit{\boldsymbol{Q}}}^{T}}
$
(13)
证明:对于满足$||\mathit{\boldsymbol{\hat{R}}}|{{|}_{\mathcal{F}}}=\sum\nolimits_{{{a}_{i}}\in \mathcal{F}}{|{{c}_{i}}|},{{a}_{i}}=\mathit{\boldsymbol{A}}{{\mathit{\boldsymbol{x}}}_{i}}\mathit{\boldsymbol{z}}_{i}^{T}{{\mathit{\boldsymbol{B}}}^{T}}$的所有$\mathit{\boldsymbol{\hat{R}}}=\sum\nolimits_{{{a}_{i}}\in \mathcal{F}}{{{c}_{i}}}{{a}_{i}}$, 我们可以构造P和Q矩阵的第i行分别为
$
{{\mathit{\boldsymbol{p}}}_{i}}=\sqrt{|{{c}_{i}}|}\mathit{\boldsymbol{A}}{{\mathit{\boldsymbol{x}}}_{i}},{{\mathit{\boldsymbol{q}}}_{i}}=\sqrt{|{{c}_{i}}|}\mathit{\boldsymbol{B}}{{\mathit{\boldsymbol{z}}}_{i}}.||{{\mathit{\boldsymbol{A}}}^{-1}}\mathit{\boldsymbol{P}}||_{F}^{2}=\sum\limits_{i}{||{{\mathit{\boldsymbol{A}}}^{-1}}{{\mathit{\boldsymbol{p}}}_{i}}||_{2}^{2}}=\\
\sum\limits_{i}{||{{\mathit{\boldsymbol{A}}}^{-1}}\sqrt{|{{c}_{i}}|}\mathit{\boldsymbol{A}}{{\mathit{\boldsymbol{x}}}_{i}}||_{2}^{2}}=\sum\limits_{i}{\sqrt{|{{c}_{i}}|}||{{\mathit{\boldsymbol{A}}}^{-1}}\mathit{\boldsymbol{A}}{{\mathit{\boldsymbol{x}}}_{i}}||_{2}^{2}}=\sum\nolimits_{i}{|{{c}_{i}}|}.
$
相似地, 我们可得出$||{\mathit{\boldsymbol{B}}^{ - 1}}\mathit{\boldsymbol{Q}}||_F^2 = \sum\nolimits_i {|{c_i}|} $.
由$||\mathit{\boldsymbol{\hat{R}}}|{{|}_{\mathcal{F}}}=\sum\nolimits_{{{a}_{i}}\in \mathcal{F}}{|{{c}_{i}}|} $可知, $||\mathit{\boldsymbol{\hat{R}}}|{{|}_{\mathcal{F}}}>\frac{1}{2}(||{{\mathit{\boldsymbol{A}}}^{-1}}\mathit{\boldsymbol{P}}||_{F}^{2}+||{{\mathit{\boldsymbol{B}}}^{-1}}\mathit{\boldsymbol{Q}}||_{F}^{2})$不成立.
由$\mathit{\boldsymbol{\hat{R}}}=\mathit{\boldsymbol{P}}{{\mathit{\boldsymbol{Q}}}^{T}}$可构造xi=A-1Pi/||A-1Pi||2, zi=B-1qi/||B-1qi||2, ci=||A-1Pi||2||B-1qi||2.
由此可得${{\mathit{\boldsymbol{p}}}_{i}}\mathit{\boldsymbol{q}}_{i}^{T}={{c}_{i}}\mathit{\boldsymbol{A}}{{\mathit{\boldsymbol{x}}}_{i}}{{\mathit{\boldsymbol{z}}}_{i}}{{\mathit{\boldsymbol{B}}}^{T}},\mathit{\boldsymbol{\hat{R}}}=\sum\nolimits_{i}{{{c}_{i}}\mathit{\boldsymbol{A}}{{\mathit{\boldsymbol{x}}}_{i}}\mathit{\boldsymbol{z}}_{i}^{T}}{{\mathit{\boldsymbol{B}}}^{T}}$.
由均值不等式可得出$|{{c}_{i}}|=||{{\mathit{\boldsymbol{A}}}^{-1}}{{\mathit{\boldsymbol{p}}}_{i}}|{{|}_{2}}||{{\mathit{\boldsymbol{B}}}^{-1}}{{\mathit{\boldsymbol{q}}}_{i}}|{{|}_{2}}\le \frac{1}{2}(||{{\mathit{\boldsymbol{A}}}^{-1}}{{\mathit{\boldsymbol{p}}}_{i}}||_{2}^{2}+||{{\mathit{\boldsymbol{B}}}^{-1}}{{\mathit{\boldsymbol{q}}}_{i}}||_{2}^{2})$.
进一步得出$\sum\nolimits_{i}{|{{c}_{i}}|}\le \frac{1}{2}(\sum\nolimits_{i}{||{{\mathit{\boldsymbol{A}}}^{-1}}{{\mathit{\boldsymbol{p}}}_{i}}||_{2}^{2}}+\sum\nolimits_{i}{||{{\mathit{\boldsymbol{B}}}^{-1}}{{\mathit{\boldsymbol{q}}}_{i}}||_{2}^{2}})$.
因此可得$\sum\nolimits_{i}{|{{c}_{i}}|}\le \frac{1}{2}(\sum\nolimits_{i}{||{{\mathit{\boldsymbol{A}}}^{-1}}{{\mathit{\boldsymbol{p}}}_{i}}||_{F}^{2}}+\sum\nolimits_{i}{||{{\mathit{\boldsymbol{B}}}^{-1}}{{\mathit{\boldsymbol{q}}}_{i}}||_{F}^{2}}) $.
又因$||\mathit{\boldsymbol{\hat{R}}}|{{|}_{\mathcal{F}}}=\inf \sum\nolimits_{{{a}_{i}}\in \mathcal{F}}{|{{c}_{i}}|}$, 最终可得定理成立.
推论1. 联合正则化是一种加权的原子范数.
证明:由上述定理可得$ ||{{\mathit{\boldsymbol{A}}}^{-1}}\mathit{\boldsymbol{P}}||_{F}^{2}=tr[{{\mathit{\boldsymbol{P}}}^{T}}{{({{\mathit{\boldsymbol{A}}}^{-1}})}^{T}}{{\mathit{\boldsymbol{A}}}^{-1}}\mathit{\boldsymbol{P}}],||{{\mathit{\boldsymbol{B}}}^{-1}}\mathit{\boldsymbol{Q}}||_{F}^{2}=tr[{{\mathit{\boldsymbol{Q}}}^{T}}{{({{\mathit{\boldsymbol{B}}}^{-1}})}^{T}}{{\mathit{\boldsymbol{B}}}^{-1}}\mathit{\boldsymbol{Q}}]$.
对公式(10)中的矩阵${{\mathit{\boldsymbol{\tilde{L}}}}^{p}}$和${{\mathit{\boldsymbol{\tilde{L}}}}^{q}}$分别进行特征分解, 可得${{\mathit{\boldsymbol{\tilde{L}}}}^{p}}={{\mathit{\boldsymbol{U}}}_{p}}{{\mathit{\boldsymbol{S}}}_{p}}\mathit{\boldsymbol{U}}_{p}^{T},{{\mathit{\boldsymbol{\tilde{L}}}}^{q}}={{\mathit{\boldsymbol{U}}}_{q}}{{\mathit{\boldsymbol{S}}}_{q}}\mathit{\boldsymbol{U}}_{q}^{T}$.
将其带入$tr({{\mathit{\boldsymbol{P}}}^{T}}{{\mathit{\boldsymbol{\tilde{L}}}}^{p}}\mathit{\boldsymbol{P}}),tr({{\mathit{\boldsymbol{Q}}}^{T}}{{\mathit{\boldsymbol{\tilde{L}}}}^{q}}\mathit{\boldsymbol{Q}})$, 可得$tr({{\mathit{\boldsymbol{P}}}^{T}}{{\mathit{\boldsymbol{\tilde{L}}}}^{p}}\mathit{\boldsymbol{P}})=tr({{\mathit{\boldsymbol{P}}}^{T}}{{\mathit{\boldsymbol{U}}}_{p}}{{\mathit{\boldsymbol{S}}}_{p}}\mathit{\boldsymbol{U}}_{p}^{T}\mathit{\boldsymbol{P}}),tr({{\mathit{\boldsymbol{Q}}}^{T}}{{\mathit{\boldsymbol{\tilde{L}}}}^{q}}\mathit{\boldsymbol{Q}})=tr({{\mathit{\boldsymbol{Q}}}^{T}}{{\mathit{\boldsymbol{U}}}_{q}}{{\mathit{\boldsymbol{S}}}_{q}}\mathit{\boldsymbol{U}}_{q}^{T}\mathit{\boldsymbol{Q}})$.
令$\mathit{\boldsymbol{A}}={{\mathit{\boldsymbol{U}}}_{p}}\mathit{\boldsymbol{S}}_{P}^{-1/2},\mathit{\boldsymbol{B}}={{\mathit{\boldsymbol{U}}}_{q}}\mathit{\boldsymbol{S}}_{q}^{-1/2}$, 将其分别带入$||{{\mathit{\boldsymbol{A}}}^{-1}}\mathit{\boldsymbol{P}}||_{F}^{2},||{{\mathit{\boldsymbol{B}}}^{-1}}\mathit{\boldsymbol{Q}}||_{F}^{2}$, 可得:
$
||{{\mathit{\boldsymbol{A}}}^{-1}}\mathit{\boldsymbol{P}}||_{F}^{2}=tr({{\mathit{\boldsymbol{P}}}^{T}}{{\mathit{\boldsymbol{U}}}_{p}}{{\mathit{\boldsymbol{S}}}_{p}}\mathit{\boldsymbol{U}}_{p}^{T}\mathit{\boldsymbol{P}}),||{{\mathit{\boldsymbol{B}}}^{-1}}\mathit{\boldsymbol{Q}}||_{F}^{2}=tr({{\mathit{\boldsymbol{Q}}}^{T}}{{\mathit{\boldsymbol{U}}}_{q}}{{\mathit{\boldsymbol{S}}}_{q}}\mathit{\boldsymbol{U}}_{q}^{T}\mathit{\boldsymbol{Q}})
$
因此可得出$tr({{\mathit{\boldsymbol{P}}}^{T}}{{\mathit{\boldsymbol{\tilde{L}}}}^{p}}\mathit{\boldsymbol{P}})=||{{\mathit{\boldsymbol{A}}}^{-1}}\mathit{\boldsymbol{P}}||_{F}^{2},tr({{\mathit{\boldsymbol{Q}}}^{T}}{{\mathit{\boldsymbol{\tilde{L}}}}^{q}}\mathit{\boldsymbol{Q}})=||{{\mathit{\boldsymbol{B}}}^{-1}}\mathit{\boldsymbol{Q}}||_{F}^{2}$.
根据定理1可得出, 本文所提出的联合正则化是一种加权原子范数.
在矩阵分解求解模型参数时, 根据文献[
文献[
$
\begin{align}
& f=\frac{1}{2}\sum\limits_{u=1}^{m}{\sum\limits_{j\in {{\mathcal{P}}_{u}}}{{{({{{\mathit{\boldsymbol{\hat{R}}}}}_{uj}}-{{\mathit{\boldsymbol{R}}}_{uj}})}^{2}}}}+\frac{1}{2}\{tr({{\mathit{\boldsymbol{P}}}^{T}}{{{\mathit{\boldsymbol{\tilde{L}}}}}^{p}}\mathit{\boldsymbol{P}})+tr({{\mathit{\boldsymbol{Q}}}^{T}}{{{\mathit{\boldsymbol{\tilde{L}}}}}^{q}}\mathit{\boldsymbol{Q}})\}+ \\
& \frac{\lambda }{2}\left( \sum\limits_{u=1}^{m}{|{{\mathcal{P}}_{u}}{{|}^{-\frac{1}{2}}}\mathit{\boldsymbol{b}}_{p}^{u}\mathit{\boldsymbol{b}}_{p}^{u}}+\sum\limits_{j=1}^{n}{|{{\mathcal{Q}}_{j}}{{|}^{-\frac{1}{2}}}\mathit{\boldsymbol{b}}_{q}^{j}\mathit{\boldsymbol{b}}_{q}^{j}}+\sum\limits_{k\in {{\mathcal{P}}_{u}}}{|{{\mathcal{Q}}_{k}}{{|}^{-\frac{1}{2}}}||{{\mathit{\boldsymbol{y}}}_{k}}||_{2}^{2}} \right) \\
\end{align}
$
(14)
其中, bp, bq分别表示用户和物品的偏置向量, $\mathit{\boldsymbol{b}}_p^u,\mathit{\boldsymbol{b}}_q^j$分别表示用户u和物品j的偏置项.
每个物品k关联的一个隐式反馈向量yk∈$\mathbb{R}$d用于建模隐式反馈信息对用户的潜在特征向量的影响, 此时, ${{\mathit{\boldsymbol{\hat{R}}}}_{uj}}$由公式(15)可得:
$
{{\mathit{\boldsymbol{\hat{R}}}}_{uj}}=\mathit{\boldsymbol{b}}_{p}^{u}+\mathit{\boldsymbol{b}}_{q}^{j}+\mu +{{({{\mathit{\boldsymbol{p}}}_{u}}+|{{\mathcal{P}}_{u}}{{|}^{-\frac{1}{2}}}\sum\nolimits_{k\in {{\mathcal{P}}_{u}}}{{{\mathit{\boldsymbol{y}}}_{k}}})}^{T}}{{q}_{j}}
$
(15)
其中, μ表示全局平均评分.
图 1
Fig. 1
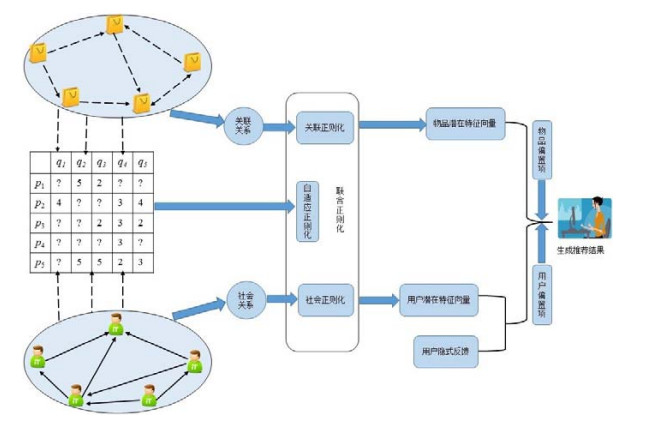
Fig. 1 An illustration of co-regularized matrix factorization recommendation
图 1 基于联合正则化的矩阵分解推荐示意图
2.3 CRMF算法
本文使用SGD求解联合正则化的矩阵分解模型的参数, 由此可得出CRMF算法的详细流程见
表 1(Table 1)
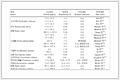
Table 1 CRMF algorithm
表 1 CRMF算法

Table 1 CRMF algorithm
表 1 CRMF算法
在$\partial f/\partial \mathit{\boldsymbol{b}}_{p}^{u},\partial f/\partial \mathit{\boldsymbol{b}}_{q}^{j}$, ∂f/∂yk, ∂f1/∂Pu, ∂f2/∂Pu, ∂f1/∂qj, ∂f2/∂qj的计算:
$
\begin{align}
& \partial f/\partial \mathit{\boldsymbol{b}}_{p}^{u}=\sum\nolimits_{j\in {{\mathcal{P}}_{u}}}{{{e}_{uj}}}+\lambda |{{\mathcal{P}}_{u}}{{|}^{-\frac{1}{2}}}\mathit{\boldsymbol{b}}_{p}^{u},\partial f/\partial \mathit{\boldsymbol{b}}_{q}^{j}=\sum\nolimits_{u\in {{\mathcal{Q}}_{j}}}{{{e}_{uj}}}+\lambda |{{\mathcal{Q}}_{j}}{{|}^{-\frac{1}{2}}}\mathit{\boldsymbol{b}}_{q}^{j},\forall k\in {{\mathcal{P}}_{u}},\partial f/\partial {{\mathit{\boldsymbol{y}}}_{k}} \\
& =\sum\nolimits_{k\in {{\mathcal{P}}_{u}}}{{{e}_{uj}}|{{\mathcal{P}}_{u}}{{|}^{-\frac{1}{2}}}{{\mathit{\boldsymbol{q}}}_{j}}}+\lambda |{{\mathcal{Q}}_{k}}{{|}^{-\frac{1}{2}}}{{\mathit{\boldsymbol{y}}}_{k}}, \\
& {\text{令}}{{f}_{1}}=\frac{1}{2}\sum\limits_{u=1}^{m}{\sum\limits_{j\in {{\mathcal{P}}_{u}}}{e_{uj}^{2}}}+\frac{\lambda }{2}\left( \sum\limits_{u=1}^{m}{|{{\mathcal{P}}_{u}}{{|}^{-\frac{1}{2}}}||{{\mathit{\boldsymbol{p}}}_{u}}||_{2}^{2}}+\sum\limits_{j=1}^{n}{|{{\mathcal{Q}}_{j}}{{|}^{-\frac{1}{2}}}||{{\mathit{\boldsymbol{q}}}_{j}}||_{2}^{2}} \right), \\
& {{f}_{2}}=\frac{\beta }{2}tr({{\mathit{\boldsymbol{P}}}^{T}}{{\mathit{\boldsymbol{L}}}^{p}}\mathit{\boldsymbol{P}})+\frac{\alpha }{2}tr({{\mathit{\boldsymbol{Q}}}^{T}}{{\mathit{\boldsymbol{L}}}^{q}}\mathit{\boldsymbol{Q}}), \\
& \partial {{f}_{1}}/\partial {{\mathit{\boldsymbol{p}}}_{u}}=\sum\nolimits_{j\in {{\mathcal{P}}_{u}}}{{{e}_{uj}}{{\mathit{\boldsymbol{q}}}_{j}}}+\lambda |{{\mathcal{P}}_{u}}{{|}^{-\frac{1}{2}}}{{\mathit{\boldsymbol{p}}}_{u}},\partial {{f}_{2}}/\partial {{\mathit{\boldsymbol{p}}}_{u}}=\frac{\beta }{2}(\sum\nolimits_{v\in \mathcal{S}_{u}^{+}}{{{\mathit{\boldsymbol{S}}}_{uv}}({{\mathit{\boldsymbol{p}}}_{u}}-{{\mathit{\boldsymbol{p}}}_{v}})} \\
& +\sum\nolimits_{g\in \mathcal{S}_{u}^{-}}{{{\mathit{\boldsymbol{S}}}_{ug}}({{\mathit{\boldsymbol{p}}}_{u}}-{{\mathit{\boldsymbol{p}}}_{g}})}), \\
& \partial {{f}_{1}}/\partial {{\mathit{\boldsymbol{q}}}_{j}}=\sum\nolimits_{u\in {{\mathcal{Q}}_{j}}}{{{e}_{uj}}({{\mathit{\boldsymbol{p}}}_{u}}+\sum\nolimits_{k\in {{\mathcal{P}}_{u}}}{{\mathit{\boldsymbol{y}}_{k}}})}+\lambda |{{\mathcal{Q}}_{j}}{{|}^{-\frac{1}{2}}}{{\mathit{\boldsymbol{q}}}_{j}},\partial {{f}_{2}}/\partial {{\mathit{\boldsymbol{q}}}_{j}}= \\
& \frac{\alpha }{2}(\sum\nolimits_{i\in \mathcal{W}_{j}^{+}}{{{\mathit{\boldsymbol{W}}}_{ji}}({{\mathit{\boldsymbol{q}}}_{j}}-{{\mathit{\boldsymbol{q}}}_{i}})}+\sum\nolimits_{o\in \mathcal{W}_{j}^{-}}{{{\mathit{\boldsymbol{W}}}_{oj}}({{\mathit{\boldsymbol{q}}}_{j}}-{{\mathit{\boldsymbol{q}}}_{o}})}), \\
\end{align}
$
其中, ${{e}_{uj}}={{\mathit{\boldsymbol{\hat{R}}}}_{uj}}-{{\mathit{\boldsymbol{R}}}_{uj}},\mathcal{S}_{u}^{-}$表示与用户u建立社会关系的用户集, $\mathcal{W}_j^ - $表示与物品j相关联的物品集.CRMF算法的时间复杂度主要包括对目标函数f和各梯度变量的计算.计算目标函数f的时间复杂度为O(d|$\mathcal{R}^{tr}$|+d| $\mathcal{S}$|+d|$\mathcal{W}$|), |$\mathcal{S}$|表示社会关系数量, |$\mathcal{W}$|表示关联关系数量.计算梯度$\partial f/\partial \mathit{\boldsymbol{b}}_{p}^{u},\partial f/\partial \mathit{\boldsymbol{b}}_{q}^{j}$, ∂f1/∂Pu, ∂f2/∂Pu, ∂f1/∂qj, ∂f2/∂qj, ∂f/∂yk的时间复杂度分别为O(d|$\mathcal{R}^{tr}$|), O(d|$\mathcal{R}^{tr}$|), O(d|$\mathcal{R}^{tr}$|), O(d|$\mathcal{S}$|), O(d|$\mathcal{R}^{tr}$|), O(d|$\mathcal{W}$|), $O(d|{\mathcal{R}^{tr}}|\bar r)$, 其中, $\bar r$表示物品平均被评分的数量.由此可得算法迭代一次的复杂度.由于$\bar r \ll \min (|{\mathcal{R}^{tr}}|,|\mathcal{S}|,|\mathcal{W}|)$, 因此算法的整体复杂度与评分数量、社会关系数量、关联关系数量呈线性相关, 可用于处理大规模数据.
3 实验结果及分析
3.1 数据集及实验环境
为了对比不同信息对推荐结果的影响, 本文使用4个含有评分信息和社会关系的数据集对提出的算法进行验证, 分别为Flixster(http://www.cs.ubc.ca/~jamalim/datasets/), Epinions(http://www.trustlet.org/epinions.html), Ciao(http://www.cse.msu.edu/~tangjili/trust.html),FilmTrust(http://www.librec.net/datasets.html).Flixster是基于社交网络的电影评论网站, 用户可对电影做出[0.5, 5.5]范围内的评分, 步长是0.5.Ciao是物品评论网站, 用户可对物品做出[1, 5]范围内的评分.FilmTrust是基于信任关系的电影推荐网站, 用户可根据自己的喜好对电影做出[0.5, 4]范围内的评分, 其步长是0.5.Epinions是物品评论数据集, 包含40 163个用户和139 738个物品上的664 824个评分, 该数据集非常接近实际应用的数据量, 因此它可用于考察模型的实际性能.实验中所使用的4个数据集的统计特性见
表 2(Table 2)

Table 2 Statistics of the four datasets
表 2 4个数据集的统计特性
信息
Epinions
Flixster
Ciao
FilmTrust
用户数量
40 163
53 213
17 615
1 508
物品数量
139 738
18 197
16 121
2 071
评分记录
664 824
409 803
72 665
35 497
社会关系
487 183
655 054
40 133
1 853
Table 2 Statistics of the four datasets
表 2 4个数据集的统计特性
本文将数据集分成训练集和测试集, 训练集用于学习推荐算法中的参数, 测试集用于评估推荐算法的准确性.在实验中, 按照4:1的比例将4个数据集随机地分成训练集和测试集.本文的实验是在Windows 7操作系统, 64G内存, Intel(R) Xeon(R) CPU E5-2620 0@2.00GHz的机器上进行, 实验程序基于Java语言和集成开发工具Eclipse4.5实现.
3.2 评价指标
为了评估推荐算法的性能, 本文使用平均绝对误差(mean absolute error, 简称MAE)和均方根误差(root mean squared error, 简称RMSE)作为实验结果的评价指标, 两种评价指标的计算方式如公式(16)和公式(17).通过计算预测评分与真实评分的差别来衡量推荐结果的准确性, 其值越小, 推荐准确性越高.
$
MAE = \frac{1}{{|{\mathcal{R}^{te}}|}}\sum\limits_{(u,j) \in {\mathcal{R}^{te}}} {|{R_{uj}} - {{\hat R}_{uj}}|}
$
(16)
$
RMSE = \sqrt {\frac{1}{{|{\mathcal{R}^{te}}|}}\sum\limits_{(u,j) \in {\mathcal{R}^{te}}} {{{({R_{uj}} - {{\hat R}_{uj}})}^2}} }
$
(17)
其中, $\mathcal{R}^{te}$表示测试集, |$\mathcal{R}^{te}$|表示测试集中评分的数量.
3.3 对比算法及超参数设定
在实验中, 我们选择基于Librec(http://www.librec.net)平台来实现并验证CRMF算法.为了验证社会关系和关联关系在推荐过程中所起的作用, 本文选取了6种主流的推荐算法与CRMF进行了详细对比, 并在d=10.
表 3(Table 3)

Table 3 Hyper-Parameter settings of compared algorithms
表 3 对比算法的超参数设置
Algorithms
Epinions
Flixster
Ciao
FilmTrust
PMF
λU=λV=0.01
λU=λV=0.1
λU=λV=0.1
λU=λV=0.1
SoRec
λU=λV=0.001, λC=1
λU=λV=0.001, λC=0.001
λU=λV=0.001, λC=0.01
λU=λV=0.001, λC=0.1
SoReg
λU=λV=0.001, β=0.1
λU=λV=0.001, β=0.01
λU=λV=0.001, β=0.01
λU=λV=0.001, β=0.1
SociaMF
λU=λV=0.001, λT=5
λU=λV=0.001, λT=1
λU=λV=0.001, λT=1
λU=λV=0.001, λT=1
TrustMF
λU=λV=0.001, λT=1
λU=λV=0.001, λT=1
λU=λV=0.001, λT=1
λU=λV=0.001, λT=1
SVD++
λb=λU=λV=0.35
λb=λU=λV=0.03
λb=λU=λV=0.1
λb=λU=λV=0.1
CRMF
λ=0.4, ρ=80, α=0.1, β=0.1
λ=0.8, ρ=50, α=0.1, β=0.01
λ=0.4, ρ=100, α=0.01, β=0.01
λ=1, 2, ρ=20, α=0.01, β=0.1
Table 3 Hyper-Parameter settings of compared algorithms
表 3 对比算法的超参数设置
(1)PMF:由Salakhutdinov等人[提出的一种基于概率的矩阵分解推荐算法, 该算法仅考虑了用户对物品的评分信息;
(2)SoReg:由Ma等人[提出的一种基于社会关系的推荐算法, 该算法将社会关系以社会正则化的方式约束传统矩阵分解时用户潜在特征向量的学习, 使得存在社会关系的两个用户其潜在特征向量尽可能的相似;
(3)SoRec:由Ma等人[提出的一种基于社会关系的推荐算法, 该算法通过同时分解评分矩阵和用户的社会关系矩阵并且以共享用户潜在特征矩阵的方式, 学习出用户和物品的潜在特征矩阵;
(4)SociaMF:由Jamali等人[提出的一种将社交网络中的信任传播结构与PMF相结合的推荐算法, 该算法有效地考虑了直接和间接信任的用户对目标用户评分的影响;
(5)TrustMF:由Yang等人[提出的一种基于信任关系的推荐算法, 该算法合理地反映了信任用户之间的相互关系对于推荐过程中评分预测的影响;
(6)SVD++:由Koren等人[提出的一种同时考虑用户偏置、物品偏置以及用户隐式反馈信息的推荐算法, 该算法是矩阵分解中推荐精度较高的算法, 并且是当年Netflix大赛获奖者所使用的关键算法.
3.4 实验结果与分析
实验1: 不同特征向量维度下的实验结果对比.
根据文献[d=5, 10.MAE和RMSE的比较结果, MAE和RMSE的比较结果.从两个表中的实验结果可看出,
表 4(Table 4)

Table 4 Performance comparison on all users
表 4 全体用户集上的性能对比
All
Metrics
PMF
SoRec
SoReg
SociaMF
TrustMF
SVD++
CRMF
Improve (%)
Epinions
d=5
MAE
0.979
0.882
0.946
0.825
0.818
0.818
0.799
2.32
RMSE
1.290
1.114
1.245
1.070
1.069
1.057
1.043
1.32
d=10
MAE
0.909
0.884
0.896
0.826
0.819
0.818
0.797
2.56
RMSE
1.197
1.142
1.167
1.082
1.095
1.057
1.038
1.79
Flixster
d=5
MAE
0.814
0.750
0.774
0.770
0.790
0.794
0.728
5.45
RMSE
1.076
0.974
1.017
0.994
1.046
1.062
0.951
2.36
d=10
MAE
0.806
0.785
0.785
0.784
0.794
0.791
0.718
8.42
RMSE
1.063
1.018
1.034
1.009
1.061
1.048
0.947
6.14
Ciao
d=5
MAE
1.105
0.786
0.920
0.762
0.764
0.735
0.718
2.31
RMSE
1.448
0.997
1.239
0.977
0.987
0.974
0.952
2.25
d=10
MAE
0.903
0.776
0.854
0.749
0.767
0.733
0.717
2.18
RMSE
1.179
1.026
1.167
0.997
1.024
0.967
0.952
1.55
FilmTrust
d=5
MAE
0.714
0.628
0.674
0.638
0.631
0.613
0.608
0.82
RMSE
0.949
0.810
0.878
0.837
0.810
0.804
0.788
2.00
d=10
MAE
0.735
0.638
0.668
0.643
0.631
0.611
0.607
0.65
RMSE
0.968
0.831
0.875
0.844
0.819
0.802
0.787
1.87
Table 4 Performance comparison on all users
表 4 全体用户集上的性能对比
表 5(Table 5)

Table 5 Performance comparison on cold start users
表 5 冷启动用户集上的性能对比
Cold Start
Metrics
PMF
SoRec
SoReg
SociaMF
TrustMF
SVD++
CRMF
Improve (%)
Epinions
d=5
MAE
1.451
0.892
1.398
0.864
0.891
0.889
0.848
1.85
RMSE
1.770
1.138
1.735
1.133
1.125
1.162
1.078
4.18
d=10
MAE
1.153
0.846
0.986
0.857
0.853
0.891
0.847
0.70
RMSE
1.432
1.180
1.217
1.152
1.176
1.166
1.073
6.85
Flixster
d=5
MAE
1.097
0.872
1.058
0.881
0.871
0.868
0.843
2.88
RMSE
1.390
1.096
1.358
1.103
1.093
1.122
1.053
3.65
d=10
MAE
0.951
0.892
0.946
0.884
0.876
0.869
0.843
3.00
RMSE
1.206
1.144
1.201
1.112
1.102
1.112
1.052
4.54
Ciao
d=5
MAE
1.406
0.775
0.905
0.757
0.750
0.719
0.696
3.20
RMSE
1.763
0.983
1.106
0.964
0.955
0.958
0.923
3.35
d=10
MAE
1.047
0.720
0.757
0.732
0.722
0.717
0.695
3.07
RMSE
1.340
1.072
1.079
0.961
0.958
0.956
0.922
3.56
FilmTrust
d=5
MAE
0.814
0.670
0.783
0.697
0.674
0.677
0.649
3.13
RMSE
1.079
0.857
0.980
0.916
0.867
0.897
0.838
2.27
d=10
MAE
0.767
0.668
0.761
0.680
0.687
0.680
0.645
3.44
RMSE
1.009
0.853
0.958
0.907
0.900
0.905
0.841
1.41
Table 5 Performance comparison on cold start users
表 5 冷启动用户集上的性能对比
(1) 在全体用户集上, SVD++与PMF相比, 其推荐精度有了较大的提升, 这说明用户的偏置因素、物品的偏置因素以及用户的隐式反馈信息可提高算法的评分预测精度;
(2) 在全体用户集和冷启动用户集上, SoReg, SoRec, SocialMF, TrustMF与PMF相比, 其推荐精度均有了较大的提高.这说明用户的社会关系有助于提高传统矩阵分解模型的预测精度, 并有助于缓解用户的冷启动问题;
(3) 在冷启动用户集上, CRMF相比于6种对比算法其推荐精度有明显的的提升.这是因为当用户为冷启动时, 其社会关系的数量往往也较少, 此时仅依赖社会关系对推荐算法精度的提升是有限的; 但当目标物品为非冷启动时, 考虑物品之间的关联关系可提升推荐算法的评分预测精度.
实验2: 不同评分数量下的实验结果对比.
为了对比不同评分数量下各算法的效果, 本文依据训练集中用户的评分数量将用户划分为[0:10], [11:30], [31:50], [51:100], 100以上这5组, RMSE, 结果如
图 2
Fig. 2
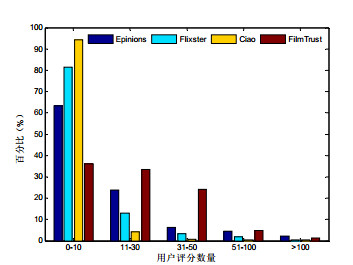
Fig. 2 Distribution of users with different ratings
图 2 不同评分数量下用户的分布
图 3
Fig. 3
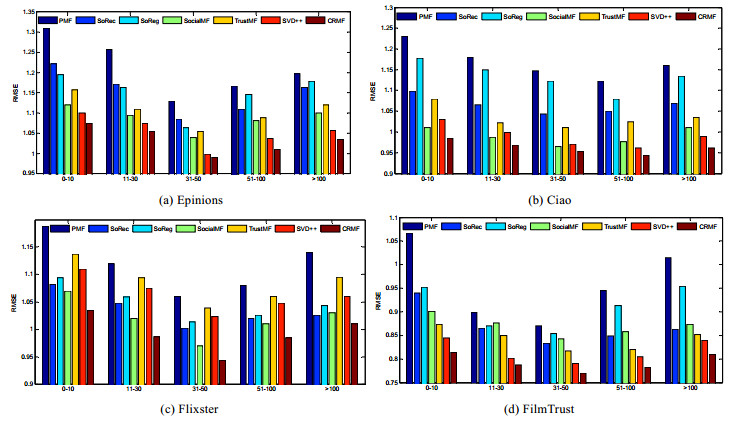
Fig. 3 Comparison on users with different ratings
图 3 不同评分数量下用户对比结果
(1) 在数据极度稀疏时(评分数量小于10), CRMF算法明显优于其他推荐算法.这因为评分数据稀疏时, 用户的社会关系往往也比较稀疏, 同时考虑物品的关联关系可提高算法的推荐精度;
(2) 随着用户评分数量的增加, CRMF及对比算法所得出的RMSE值并没有持续变小.这因为用户的评分数量较少时, 数据比较稀疏使得模型不易学习到用户的潜在特征向量.用户的评分数据过多, 用户的兴趣会发散, 这造成无法准确学习到表示用户喜好的潜在特征向量.但CRMF仍优于其他对比算法, 这因为基于联合正则化的矩阵分解模型考虑了自适应正则化, 它能够根据用户评分的数量对正则化程度进行自适应地调整, 因此使得CRMF算法可更加有效地学习出模型的参数.
实验3: 不同社会关系下的实验结果对比.
为了评估各算法在不同社会关系下的推荐精度, 依据训练集中用户拥有的社会关系数量将用户划分为[1:5], [6:10], [11:20], [21:40], [41:100], [101:500], 500以上这7组,
图 4
Fig. 4
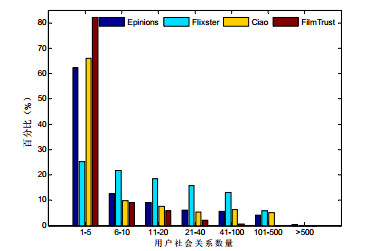
Fig. 4 Distribution of users with different social relationships
图 4 不同社会关系下用户的分布
图 5
Fig. 5
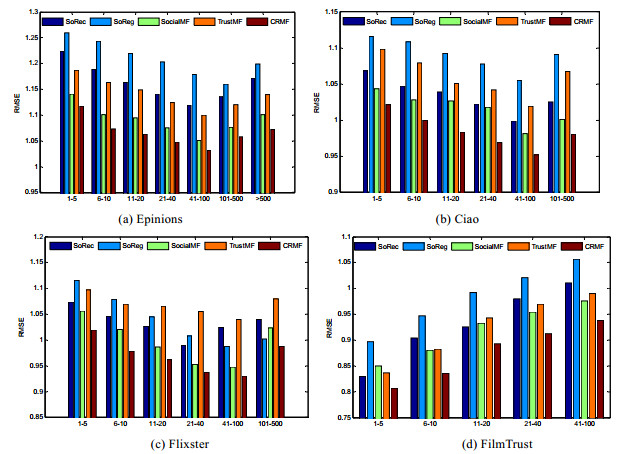
Fig. 5 Comparison on users with different social relationships
图 5 不同社会关系下用户的对比结果
(1) 在FilmTrust数据集上, 各算法的RMSE值反而随着用户拥有社会关系数量的增加而增加.根据文献[
(2) 在Epinions, Flixster及Ciao数据集上, 随着社会关系数量的增加, 5种推荐算法的RMSE值并没有持续变小.这因为当用户拥有的社会关系数量较少时, 仅靠评分数据不能有效地对用户建模而影响了算法的精度.当用户的社会关系数量过多被考虑时, 用户的兴趣过度依靠近邻的影响, 使得学习的用户的潜在特征向量会比较发散.因此仅当用户的社会关系达到一定数量时, 5种推荐算法才取得较优效果;
(3) 在4个数据集的每组用户上, CRMF均要优于其他推荐算法.这因为基于联合正则化的矩阵分解模型不仅考虑了社会关系与关联关系, 而且使用了自适应正则化, 使得矩阵分解模型能有效地对用户和物品进行建模.
实验4: 关联关系获取方法的对比.
本实验是为了评估不同的获取关联关系的方法对推荐算法精度的影响.我们首先根据皮尔逊相关系数计算两两物品之间的相似度; 然后, 为每个目标物品选择10个最相似的物品作为关联关系; 最后, 将得到的无向关联关系与SVD++结合, 得到改进的推荐算法, 简称SVD-IS.相应地, 基于本文构建的关联程度(公式(7))可为每个物品选择10个最相关的物品作为有向的关联关系.同样地, 我们将获取的有向关联关系与SVD++结合得到改进的推荐算法, 简称SVD-IR.SVD-IS, SVD-IR在相同超参数下的实验结果如
表 6(Table 6)

Table 6 Impact of item relations on RMSE
表 6 物品的关联关系对RMSE的影响
算法
数据集
Epinions
Flixster
Ciao
FilmTrust
SVD-IS
1.051
0.995
0.964
0.799
SVD-IR
1.045
0.974
0.960
0.795
Table 6 Impact of item relations on RMSE
表 6 物品的关联关系对RMSE的影响
(1) 相比于
(2) 相比于SVD-IS, SVD-IR在4个数据集上, 其推荐精度有了较高的提升.这是因为相比于无向的相似性关系, 本文方法所获取的有向关联关系更符合现实世界中物品推荐的场景.
实验5: 自适应正则化的有效性验证.
本实验是为了评估自适应正则化对于推荐算法精度的影响.我们将用户的社会关系和物品的关联关系同时与SVD++算法结合, 可得改进的推荐算法, 简称SVD-DR.SVD-DR与CRMF算法在4个数据集上的评分预测精度见
表 7(Table 7)

Table 7 Impact of adaptive regularization on RMSE
表 7 自适应正则化对RMSE的影响
算法
数据集
Epinions
Flixster
Ciao
FilmTrust
SVD-DR
1.041
0.968
0.957
0.793
CRMF
1.038
0.947
0.952
0.787
Table 7 Impact of adaptive regularization on RMSE
表 7 自适应正则化对RMSE的影响
实验6: 超参数对算法的影响.
为了说明CRMF算法的超参数对推荐结果的影响, 本文以数据集Ciao为例, 详细讨论了各超参数下的实验结果.本文设定α和β的取值为0.00001, 0.0001, 0.001, 0.01, 0.1, 0.3.超参数C的取值为0, 10, 20, 50, 100, 150, 200.超参数K的取值为0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100.从
图 6
Fig. 6
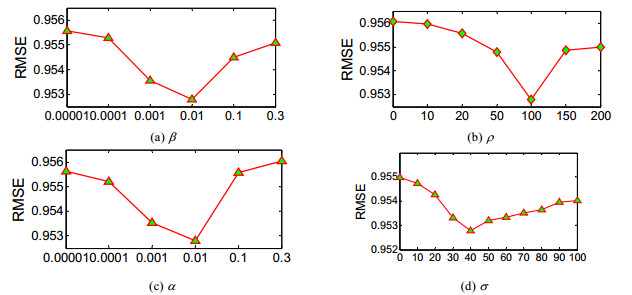
Fig. 6 Impact of hyperparameters
图 6 超参数的影响
(1)β控制着用户的社会关系对推荐结果的影响.β的变化对RMSE的影响, 其值从0.00001开始先下降, 到达某个阈值后上升.这说明用户的社会关系在CRMF算法中所占的比重直接影响推荐结果的好坏;
(2)α控制着物品之间的关联关系在推荐过程所占的比重.α的变化对RMSE值的影响, 其值从0.00001开始先下降, 到达某个阈值后上升.这表明物品之间的关联关系在CRMF算法中所占的比重直接影响推荐结果的好坏.在数据集Ciao上, 由α=β=0.01算法取得较高精度, 说明物品之间的关联关系在用户决策时也是必不可少的;
(3)ρ=0表示物品之间的关联程度等于关联规则中的置信度.从ρ值的增加, 算法的推荐精度先增加后降低.这说明物品之间关联程程度的获取, 仅当综合考虑支持度与置信度时才使得算法精度较高;
(4)σ表示物品拥有的关联关系数量.从σ=0时, 表示CRMF算法不考虑物品之间的关联关系; 随着σ值的增加, 算法的精度有所提高, 这说明本文获取物品之间关联关系的方法的有效性; 在σ=40以后, 算法的精度开始下降, 这主要是因为σ值过大会导致对目标物品引入一些关联程度较低的关联关系.
4 结论
本文首先给出一种度量物品之间关联程度的方法, 通过该方法可获取物品之间的有向关联关系; 然后将其以关联正则化的方式与自适应正则化相结合, 融入基于社会正则化的矩阵分解模型中, 提出了基于联合正则化的矩阵分解模型, 并证明了联合正则化是一种加权的原子范数.由于物品之间关联关系的获取无需物品的标签、属性等额外信息, 因此, 基于联合正则化的矩阵分解模型拥有更广泛的应用范围.在4个真实数据集上的实验表明:与主流的推荐算法相比, 本文算法不仅可缓解用户的冷启动问题, 而且能够更有效地预测不同类型用户的实际评分.
在未来的研究中, 我们将把重点放在解决物品冷启动相关的问题上.这种情况下, 如何将情境信息(时间、地理等)和物品的视觉特征融入到本文的推荐模型中, 来更好地预测目标用户对特定物品的喜好, 这也是我们下一步要改进的方向.





















 2806
2806











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








