从圆锥曲线(特指椭圆、双曲线、抛物线)的定义与标准方程出发,如何去推导与焦点相关的焦半径公式、焦点弦长公式及其相关的结论,进而加以应用.
本文不作特别说明,椭圆、双曲线、抛物线都是针对焦点在  轴上标准方程(其中抛物线考虑标准方程
轴上标准方程(其中抛物线考虑标准方程  ),
),  分别为椭圆或双曲线的左、右焦点,
分别为椭圆或双曲线的左、右焦点,  是抛物线的焦点,
是抛物线的焦点,  是相应圆锥曲线上的一点.所有的公式推导均以椭圆方程为例,且优先考虑左焦点对应的相关公式.双曲线可以完全类比椭圆的推导过程得到,特殊情况会另外说明.
是相应圆锥曲线上的一点.所有的公式推导均以椭圆方程为例,且优先考虑左焦点对应的相关公式.双曲线可以完全类比椭圆的推导过程得到,特殊情况会另外说明.
焦半径是指圆锥曲线上任意一点与焦点的连线段.对于椭圆与双曲线上的任意一点,都对应两条焦半径;对于抛物线上的任意一点,焦半径唯一存在.
设  是椭圆上任意一点,则有
是椭圆上任意一点,则有

从而焦半径

而  ,所以
,所以

其中  为椭圆的离心率.
为椭圆的离心率.

事实上,在由椭圆的定义推导椭圆方程的过程中,就已经产生了这个式子,设  满足
满足

即

分子有理化得

于是有

(1)(2)两式相加得

即为椭圆上一点  到椭圆左焦点的距离.
到椭圆左焦点的距离.
于是我们得到椭圆的焦半径公式(I):

同理有双曲线的焦半径公式(I):

当点在双曲线上的不同支上时,绝对值里面式子的正负大家可以自行讨论.
抛物线的焦半径公式可以直接由抛物线的定义得到,即

例1 椭圆  的右焦点为
的右焦点为  ,直线
,直线  与
与  轴的交点为
轴的交点为  ,在椭圆上存在点
,在椭圆上存在点  满足线段
满足线段  的垂直平分线过点
的垂直平分线过点  ,则椭圆离心率的取值范围是____.
,则椭圆离心率的取值范围是____.
正确答案是  .
.
解 设  ,则有
,则有  ,即
,即

解得

又因为  ,所以有
,所以有

两边同除 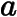 可解得
可解得

由椭圆的焦半径公式(I)知,已知椭圆上一点的横坐标,就很容易求出椭圆的焦半径长,但有时,我们知道的不是横坐标的值,而是焦半径与  轴形成的角度,我们可以从上面的焦半径公式(I)出发去推导由焦半径与
轴形成的角度,我们可以从上面的焦半径公式(I)出发去推导由焦半径与  轴正半轴所成的角
轴正半轴所成的角 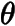 对应的焦半径公式.
对应的焦半径公式.
设  与
与  轴正半轴形成的角度为
轴正半轴形成的角度为 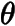 ,则有
,则有

整理得  ,于是有
,于是有

解得

同理可以推得右焦点对应的焦半径公式

其中,  是焦半径
是焦半径  与
与  轴正半轴所成的角,注意,同一个点与左焦点与右焦点连线形成的焦半径与
轴正半轴所成的角,注意,同一个点与左焦点与右焦点连线形成的焦半径与  轴正半轴所成的角不是同一个角,这是与焦半径公式(I)很不相同的地方,如图:
轴正半轴所成的角不是同一个角,这是与焦半径公式(I)很不相同的地方,如图:

于是我们得到椭圆的焦半径公式(II):

其中  为焦半径
为焦半径  与
与  轴正半轴所成的角.
轴正半轴所成的角.
对于双曲线来说,与椭圆类似可以得到双曲线的焦半径公式(II),需要注意的是,当双曲线上的点在双曲线的不同支上时,焦半径公式(I)中绝对值的正负不同,所以需要分别讨论.双曲线的焦半径公式(II):
当  在双曲线的左支时,有
在双曲线的左支时,有

当  在双曲线的右支时,有
在双曲线的右支时,有
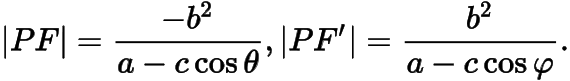
其中  为焦半径
为焦半径  与
与  轴正半轴所成的角.
轴正半轴所成的角.
抛物线的焦半径公式为:

其中 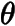 为焦半径
为焦半径  与
与  轴正半轴所成的角.
轴正半轴所成的角.
椭圆的焦半径公式(II)有两个常用的推论:
推论1 椭圆的焦点弦长公式:

其中  为椭圆的焦点弦,
为椭圆的焦点弦,  的倾斜角为
的倾斜角为 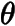 .
.
圆锥曲线的焦点弦是指过某一焦点的直线与该圆锥曲线相交得到的两个交点之间的线段.当该弦与  轴(椭圆的长轴,双曲线的实轴)垂直时,得到的弦我们称为通径.因为焦半径公式(II)是与角度相关的公式,所以我们很容易从它得到椭圆的焦点弦长公式.
轴(椭圆的长轴,双曲线的实轴)垂直时,得到的弦我们称为通径.因为焦半径公式(II)是与角度相关的公式,所以我们很容易从它得到椭圆的焦点弦长公式.
证明 设  是过椭圆左焦点
是过椭圆左焦点  的焦点弦,
的焦点弦,  的倾斜角为
的倾斜角为 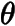 ,不妨设
,不妨设  点在
点在  轴上方,如图:
轴上方,如图:

由焦半径公式(II)知

于是
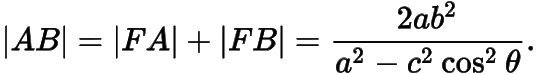
这就是椭圆的焦点弦长公式,容易知道,对于经过椭圆右焦点的弦,此公式同样适用.
事实上,对于双曲线,同样有推论1,即双曲线的焦点弦长公式:
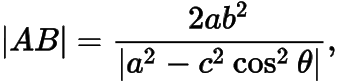
其中  为双曲线的焦点弦,
为双曲线的焦点弦,  的倾斜角为
的倾斜角为 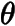 .不论
.不论  两点在双曲线的同支还是异支上,都有这个公式成立,只是绝对值中的式子正负有所不同.
两点在双曲线的同支还是异支上,都有这个公式成立,只是绝对值中的式子正负有所不同.
抛物线的焦点弦长公式更为简单,即
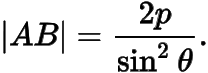
其中  是抛物线的焦点弦,
是抛物线的焦点弦,  的倾斜角为
的倾斜角为 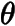 .
.
例2 椭圆  ,
,  为椭圆上四个不同的点,
为椭圆上四个不同的点,  都不和
都不和  轴垂直,且分别过
轴垂直,且分别过  ,
,  ,求证:
,求证:  为定值.
为定值.
解 设  的倾斜角为
的倾斜角为 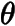 ,则
,则  的倾斜角为
的倾斜角为  ,则由焦点弦长公式知
,则由焦点弦长公式知
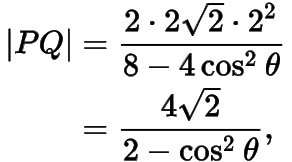

所以

为定值.
推论2 椭圆的焦点弦被焦点所分成的两段线段长的调和平均数为定值(即焦半径的倒数和为定值).
证明 由焦半径公式(I)知

于是我们知道  与
与  的调和平均数为定值,即
的调和平均数为定值,即
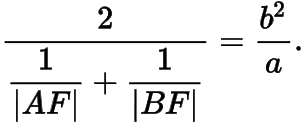
这个定值就是半通径长 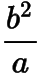 ,由均值不等式易知椭圆的所有焦点弦中,通径长最短.
,由均值不等式易知椭圆的所有焦点弦中,通径长最短.
几道练习:
练习1 椭圆  的焦点为
的焦点为  和
和 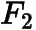 ,点
,点  在椭圆上,如果线段
在椭圆上,如果线段 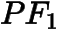 的中点在
的中点在 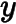 轴上,求
轴上,求  的值.
的值.
练习2 椭圆  的左右焦点分别为
的左右焦点分别为  ,过
,过  的直线交椭圆于
的直线交椭圆于  两点,过
两点,过 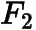 的直线交椭圆于
的直线交椭圆于  两点,
两点, 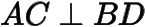 ,求四边形
,求四边形  面积的取值范围.
面积的取值范围.
答案
练习1  .
.
提示 设  ,则
,则  ,于是
,于是

于是 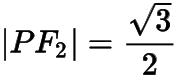 .
.
练习2  .
.
提示 设  的倾斜角为
的倾斜角为 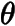 ,则
,则  的倾斜角为
的倾斜角为  ,于是
,于是

四边形  的面积
的面积

练习3



备注1 椭圆的焦半径公式(I)是从椭圆的第一定义向第二定义过渡的重要桥梁,可以通过椭圆的焦半径公式(I)去发掘椭圆的第二定义.由焦半径公式(I)知
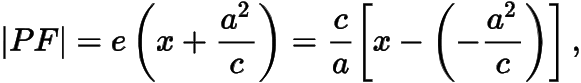
设直线 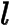 :
: 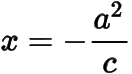 ,称为椭圆的左准线,记点
,称为椭圆的左准线,记点  到
到 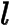 的距离为
的距离为  ,则有
,则有

即椭圆上任一点到椭圆左焦点的距离与到左准线的距离的比为定值,这个值为椭圆的离心率  .同样地有椭圆的右准线
.同样地有椭圆的右准线

于是有,椭圆上的任意点到椭圆的焦点与对应准线的距离的比值为定值  .对于双曲线也有类似的结论,双曲线的准线方程为
.对于双曲线也有类似的结论,双曲线的准线方程为

双曲线上任意点到焦点的距离与到对应准线的距离的比也为定值  ,即为双曲线的离心率.
,即为双曲线的离心率.
同时,平面上到定点  与到定直线
与到定直线 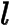 (其中
(其中  )的距离比为定值
)的距离比为定值  (其中
(其中 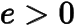 )的轨迹为椭圆、双曲线或抛物线,取决于
)的轨迹为椭圆、双曲线或抛物线,取决于  的大小.当
的大小.当  时为椭圆,当
时为椭圆,当  时为抛物线,当
时为抛物线,当  时为双曲线.
时为双曲线.
从而有圆锥曲线的统一定义:平面上到一个定点的距离与到一条定直线(其中定点不在直线上)的距离的比为定值  的点的轨迹为圆锥曲线,
的点的轨迹为圆锥曲线,  时这个定义就是抛物线的定义,当
时这个定义就是抛物线的定义,当  的范围在
的范围在  与
与  上时,对应的定义被称为椭圆与双曲线的第二定义.
上时,对应的定义被称为椭圆与双曲线的第二定义.
备注2 由椭圆的焦半径公式(II)很容易得到椭圆的极坐标方程:
以椭圆的一个焦点  为极点,以
为极点,以  轴正半轴方向为极轴方向建立极坐标系,
轴正半轴方向为极轴方向建立极坐标系,

则椭圆上任意一点  的坐标
的坐标  满足:
满足:

这就是椭圆的极坐标方程,注意如果以椭圆的右焦点为极点,  轴正方向为极轴建立极坐标系,得到的极坐标方程为
轴正方向为极轴建立极坐标系,得到的极坐标方程为

▍ 来源:综合网络
▍ 编辑:Wordwuli
▍ 声明:如有侵权,请联系删除;若需转载,请注明出处。
▍ 提示:①更多精彩内容,请点击文章标题下方的公众号名称查看;②进入公众号后,发送关键词给我,我会立即回复相关内容给您。







 本文详细探讨了椭圆、双曲线、抛物线的焦半径公式,从定义出发推导公式,并阐述了焦半径与焦点弦的关系。通过实例和推论,展示了如何运用这些公式解决相关问题,包括焦点弦长公式和焦点弦被焦点分成的两段线段的调和平均数为定值。
本文详细探讨了椭圆、双曲线、抛物线的焦半径公式,从定义出发推导公式,并阐述了焦半径与焦点弦的关系。通过实例和推论,展示了如何运用这些公式解决相关问题,包括焦点弦长公式和焦点弦被焦点分成的两段线段的调和平均数为定值。
















 976
976

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








