图像处理之模糊集合原理

supercolar

已于 2022-09-03 17:05:51 修改

阅读量1.9k

点赞数 1

分类专栏：数字图像处理文章标签：模糊集合

于 2019-10-14 09:14:08 首次发布

本文链接：https://blog.csdn.net/weixin_35732969/article/details/82830670

版权

数字图像处理专栏收录该内容

11 篇文章

订阅专栏

我的小程序：

举个例子：

我们习惯处理的集合是一种“干脆的”集合，成员要么属于这个集合（真或1），要么不属于（假或0）。例如，用Z表示所有人员的集合，我们想要定义一个“年轻人”的子集A。我们需要一个隶属度函数q，它对Z中每一个成员z赋值0或1。另外我们需要一个阈值，等于或小于该阈值的人考虑为年轻人，大于则考虑为非年轻人。下图用20岁的阈值给出了这一“干脆的”集合：

这样一个“干脆的”集合的问题或者说是不合理的地方是：年龄20岁是年轻人，只要20岁零1秒就不再是年轻人。我们希望的是年轻和非年轻之间能渐进的过渡。下图给出了另一种划分可能性：

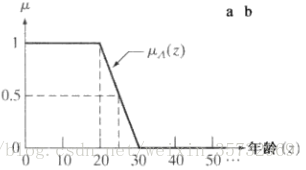
上图允许有年轻的程度，如一个50%年轻的人位于斜坡的中间，曲线的斜率引入什么是“年轻”的更加模糊的概念。

定义：令Z为元素集，z表示Z的一类元素，即Z = {z}。Z中的模糊集合A由隶属度函数 $\mu _{A}(z)$ 表征，它是与Z的元素相关的在区间[0,1]内的一个实数。 $\mu _{A}(z)$ 在z处的值表示A中z的隶属度等级， $\mu _{A}(z)$ = 1的所有z都是集合的完全成员， $\mu _{A}(z)$ =0的所有z都不是集合的成员，而 $\mu _{A}(z)$ 的值介于0和1之间的所有z是集合的部分成员。因此，模糊集合是一个由z值和相应的隶属度函数组成的序对：

$A = \{z,\mu _{A}(z)|z\in Z\}$

年龄限制为整数年时，根据上面第二幅图，则有：

A = {(1,1),(2,1),(3,1),...,(20,1),(21,0.9),(22,0.8),...,(25,0.5),(26,0.4),...,(29,0.1)}

空集：当且仅当Z中的隶属度函数等于0。

相等：模糊集合A和B相等，当且仅当对所有的 $z\in Z$ 有 $\mu _{A}(z) = \mu_{B}(z)$ 。

补集：由 $\bar{A}$ 或NOT(A)表示模糊集合A的补集，定义为其隶属度函数是 $\mu_{\bar{A}}(z) = 1-\mu_{A}(z)$ 的集合。

子集：模糊集合A是模糊集合B的子集，当且仅当对于所有的 $z\in Z$ ， $\mu_{A}(z)\leqslant \mu_{B}(z)$ 。

并集：两个模糊集合A和B的并集，具有隶属度函数 $\mu_{U}(z) = max[\mu_{A}(z),\mu_{B}(z)]$ ，表示为 $A\cup B$ 或A OR B。

交集：两个模糊集合A和B的交集，具有隶属度函数 $\mu_{I}(z) = min[\mu_{A}(z),\mu_{B}(z)]$ ，表示为 $A\cap B$ 或A AND B。

交并补的定义可用如下的图表示：

注：模糊逻辑和概率均在区间[0,1]上，但有明显的区别。以最开始的例子为例，概率的说法可能是“一个人年轻的可能性是50%”，而模糊逻辑的说法可能是“一个人在年轻人集合中的隶属度等级是0.5”。第一种说法中，我们有50%的机会知道这个人在不在年轻人的集合里。第二种说法说的是一个人的年轻程度是0.5，或者说这是一个“平均的”年轻人：不是真年轻，但也不是不年轻。模糊逻辑完全不是概率，它仅处理一个集合中隶属度等级。模糊逻辑在由含混和不精确而不是随机性表征的应用中找到了用途。

一些常用的隶属度函数：