将三角形绕点b顺时针旋转90度_中考数学查补训练专题：一文搞定"图形旋转"及相关的解题模型...

版权说明：本文非原创。发布前未联系到作者，故未针得作者同意。发布是为了帮助到更多的需要者。如有侵权请联系我们，我们将第一时间删除或按照作者的意愿处理。——编者。为了帮助到更多即将参加中考的同学，我们从网络上选取了部分精品中考数学复习资源，有些作品未联系到作者，作者或享有作者授权发布的编者在老李的平台看到您的作品请及时联系我们，我们将按照作者的意愿第一时间处理——老李：笔名，李澍；真实姓名，李树茂。代表作《中考(初中)数学120解题模型》；《中考数学必做的压轴题视图解析》(思维导图解题课件&视频解析)；《中考数学120解题模型实战演练视图解析》。

旋转类常见问题汇总

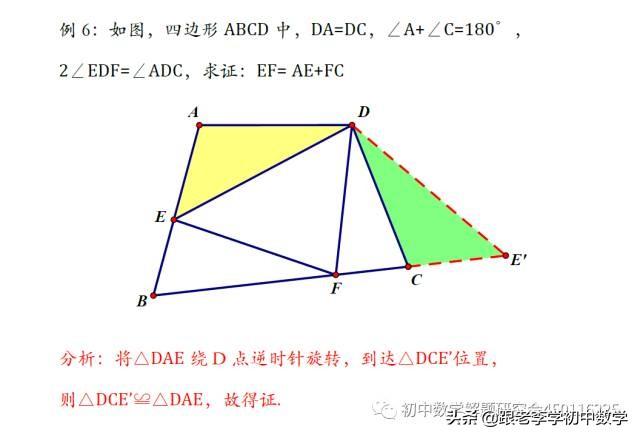
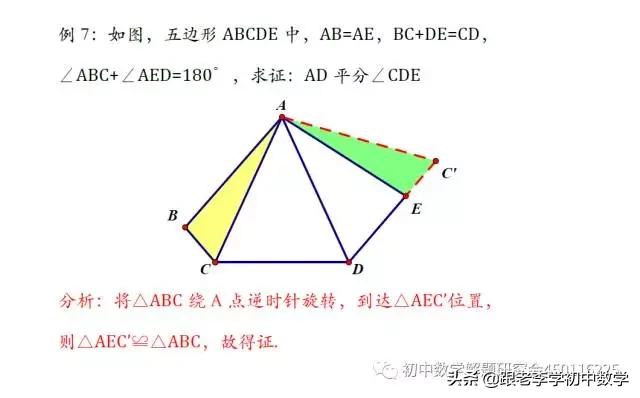
旋转的定义

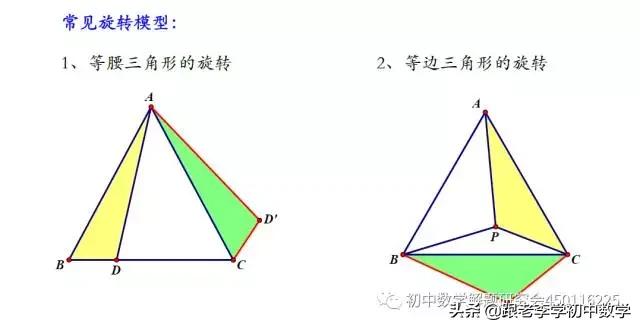
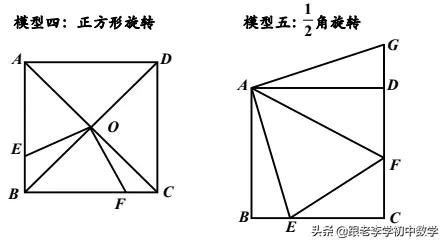
常见的几种模型

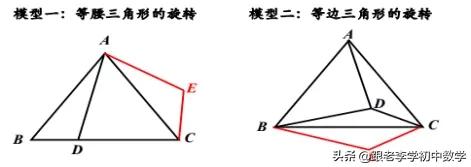
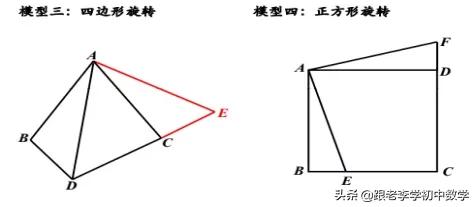
旋转类型题目举例

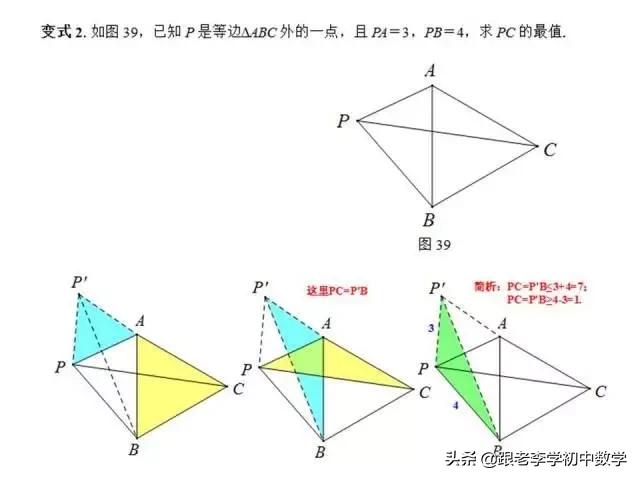
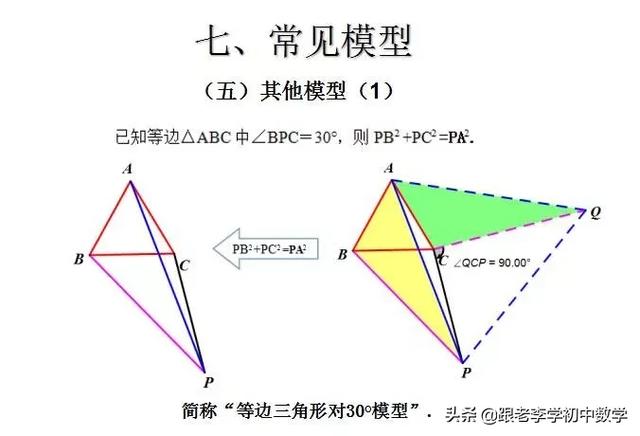
1、正三角形类型

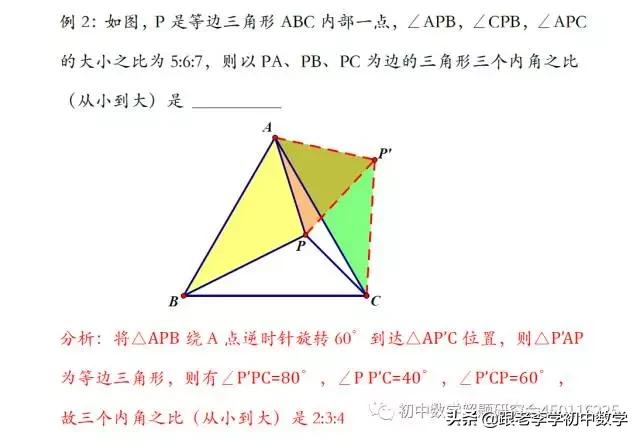
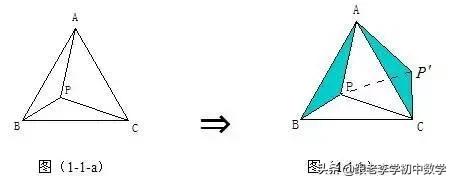
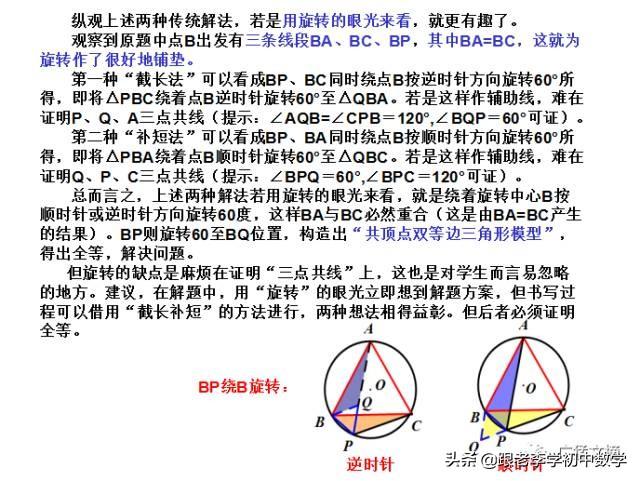
在正ΔABC中，P为ΔABC内一点，将ΔABP绕A点按逆时针方向旋转60°，使得AB与AC重合。经过这样旋转变化，将图(1-1-a)中的PA、PB、PC三条线段集中于图(1-1-b)中的一个ΔP'CP中，此时ΔP'AP也为正三角形。

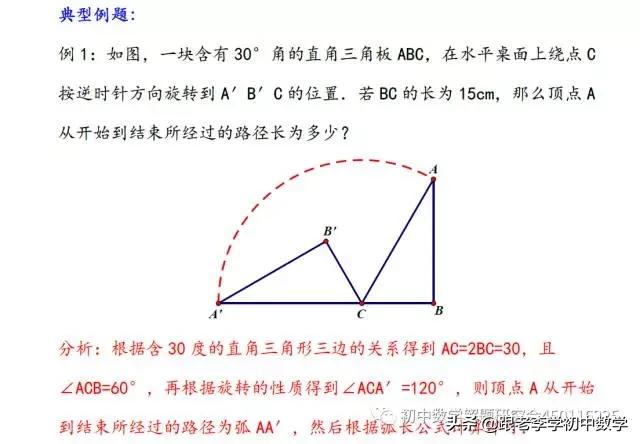
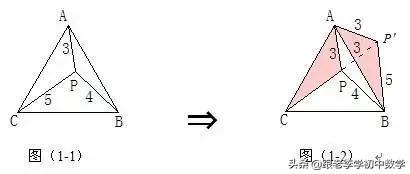
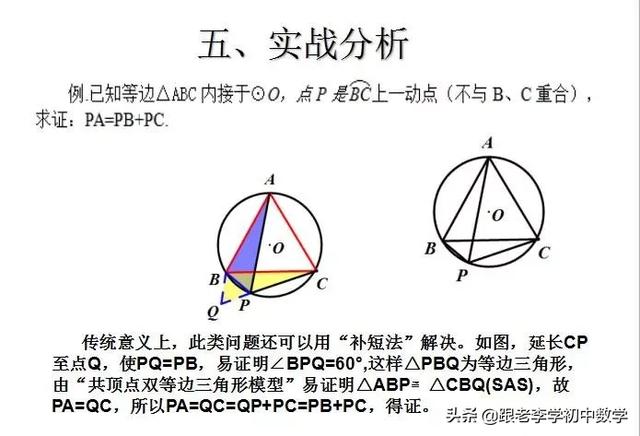
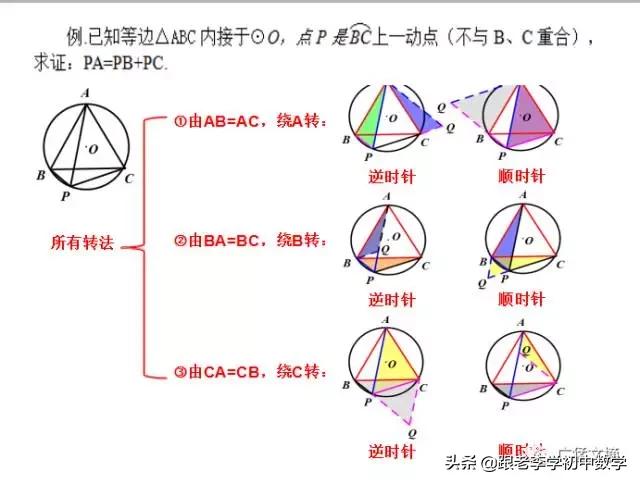
例1如图(1-1)，设P是等边ΔABC内的一点，PA=3， PB=4，PC=5，∠APB的度数是________.

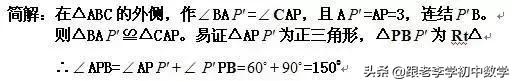
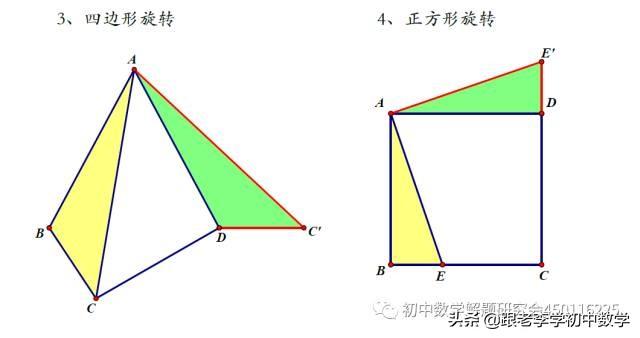
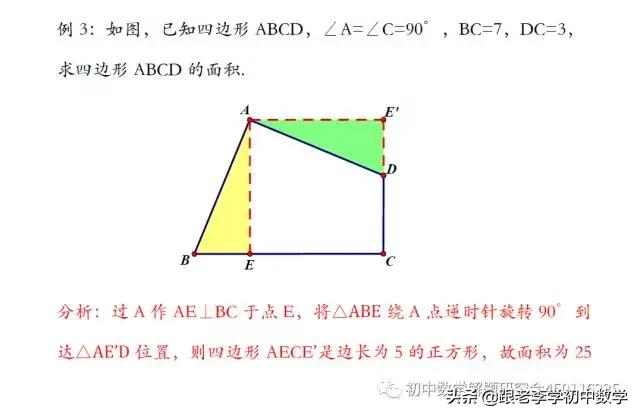
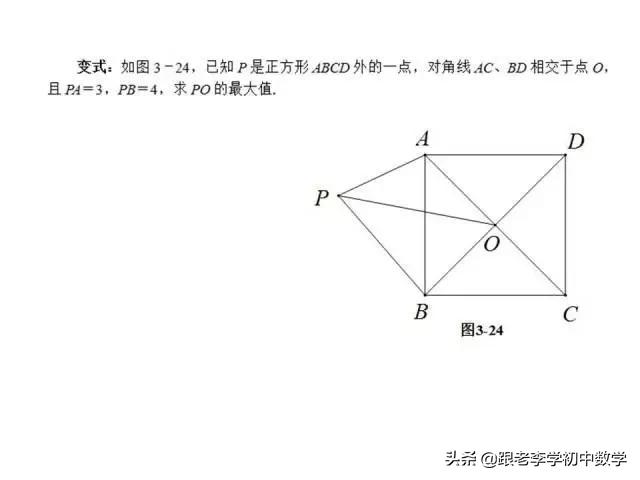
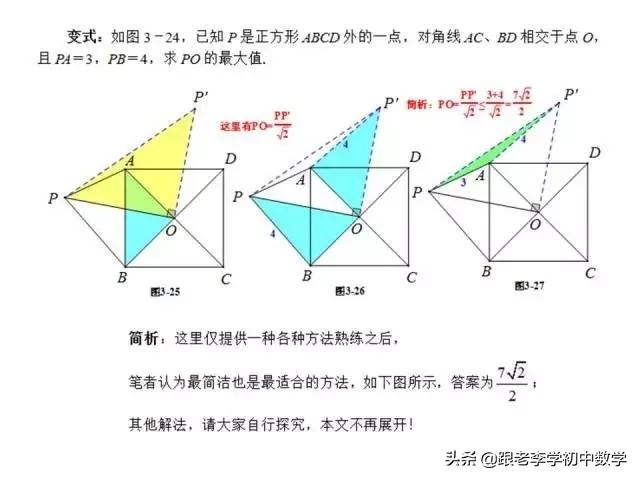
2、正方形类型

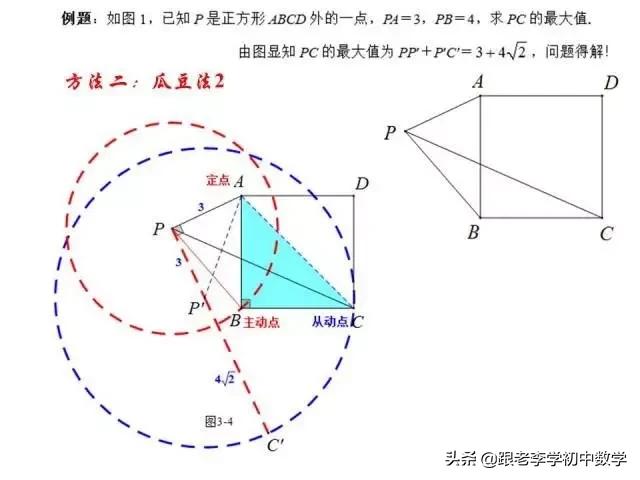
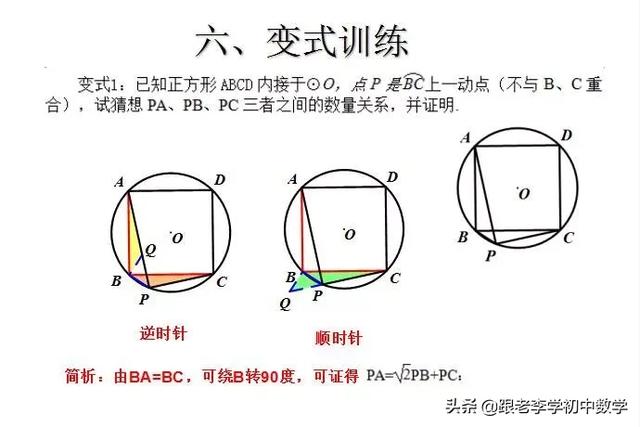
在正方形ABCD中，P为正方形ABCD内一点，将ΔABP绕B点按顺时针方向旋转90°，使得BA与BC重合。经过旋转变化，将图(2-1-a)中的PA、PB、PC三条线段集中于图(2-1-b)中的ΔCPP'中，此时ΔBPP'为等腰直角三角形。

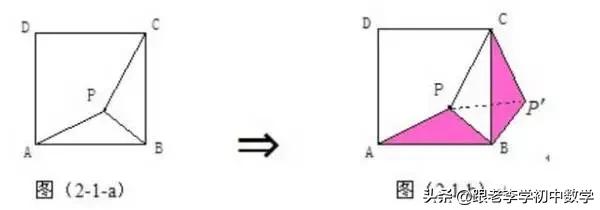
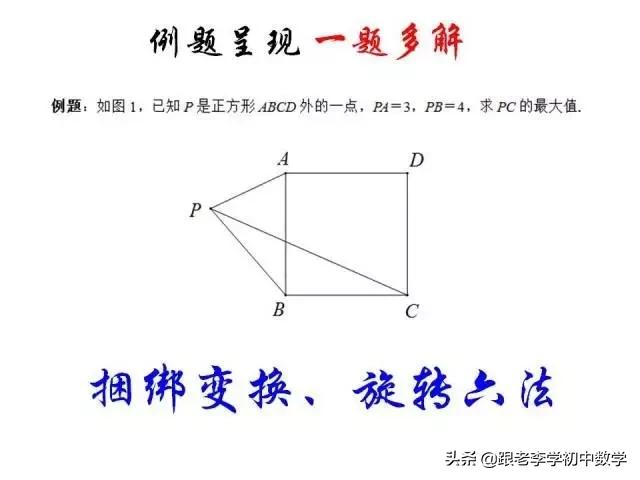
例2 如图(2-1)，P是正方形ABCD内一点，点P到正方形的三个顶点A、B、C的距离分别为PA=1，PB=2，PC=3。求正方形ABCD面积。

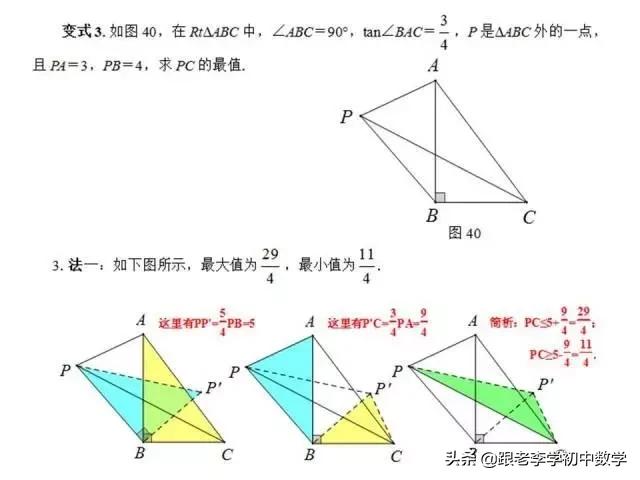
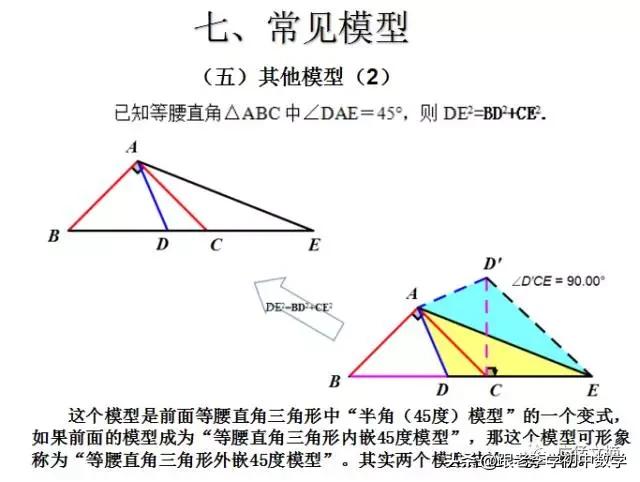
3、等腰直角三角形类型

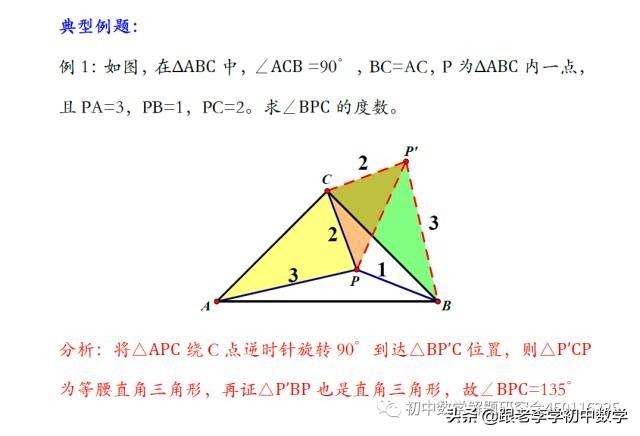
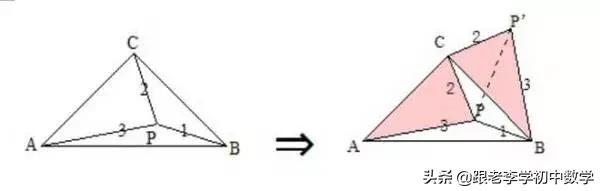
在等腰直角三角形ΔABC中，∠C=90°, P为ΔABC内一点，将ΔAPC绕C点按逆时针方向旋转90°，使得AC与BC重合。经过这样旋转变化，在图(3-1-b)中的一个ΔP'CP为等腰直角三角形。

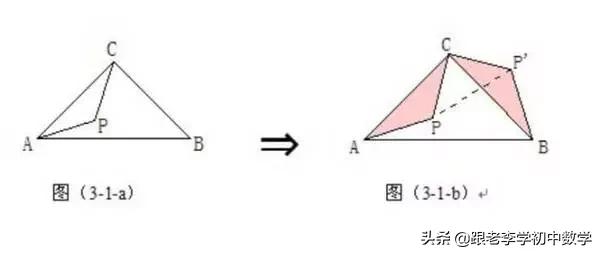
例3如图，在ΔABC中，∠ACB =90°，BC=AC，P为ΔABC内一点，且PA=3，PB=1，PC=2。求∠BPC的度数。

总结：

旋转是几何变换中的基本变换，它一般先对给定的图形或其中一部分，通过旋转，改变位置后的新组合，然后在新的图形中分析有关图形之间的关系，进而揭示条件与结论之间的内在联系，找出证题途径。

场景应用

2知识内容

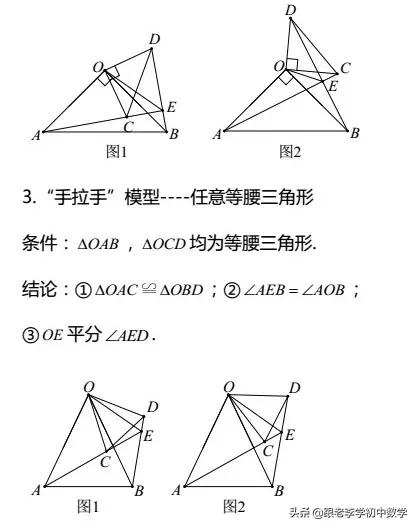
3例题讲解

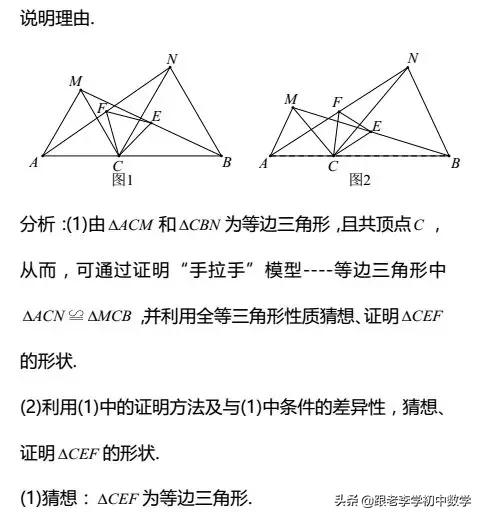
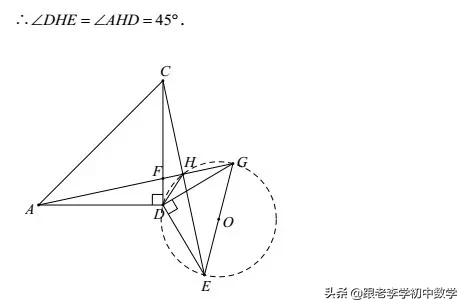
4巩固练习

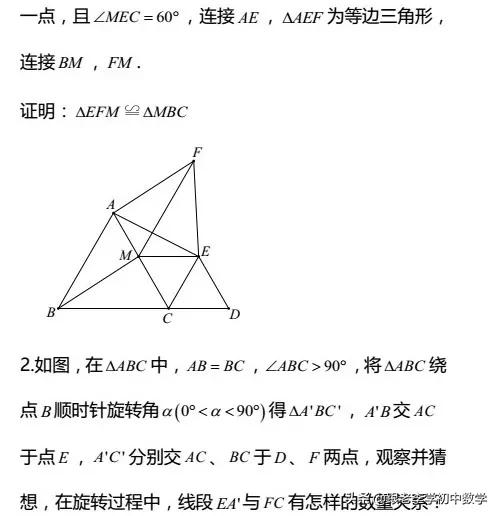
旋转，作为四大基本几何变换之一，从初一起就与大家见面了。比如角运动问题，其实就是角旋转问题。当一个角旋转一定的角度后，便产生了相交线的对顶角；当一个角旋转一定的角度，再平移一定的距离，便可以产生平行线三线八角中的内错角等。到了初二，旋转变换就更常见了，比如因旋转而产生的全等图形等。到了初三，更是用了一个章节的内容来学习旋转这个知识。

本文，依然从适合自学的角度，由浅入深地阐述旋转的本质及其变化，为学生解决旋转类试题，打下坚实的基本功。

首先，我们来看旋转的定义。课本上对旋转的定义，是图形绕着一个定点沿着一定方向旋转一定角度的运动变化。这里的定点，叫旋转中心；转动的角度，叫旋转角；转动的方向，叫旋转方向。

这里，我以线段绕端点的旋转来阐述这种图形变化。

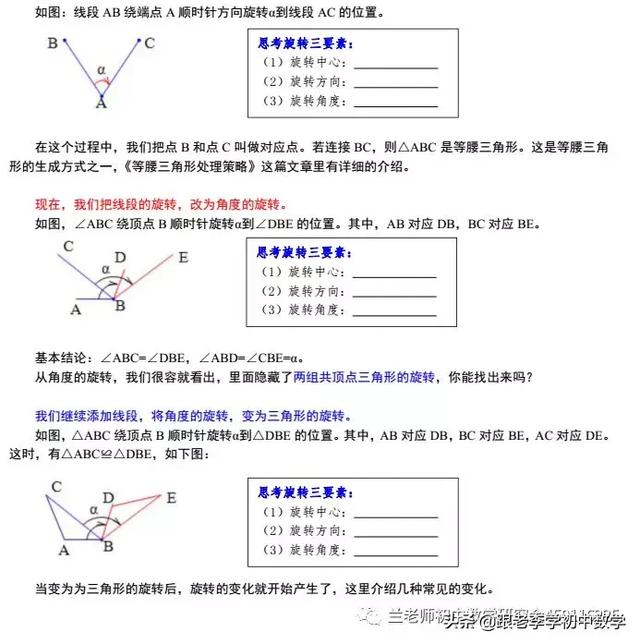
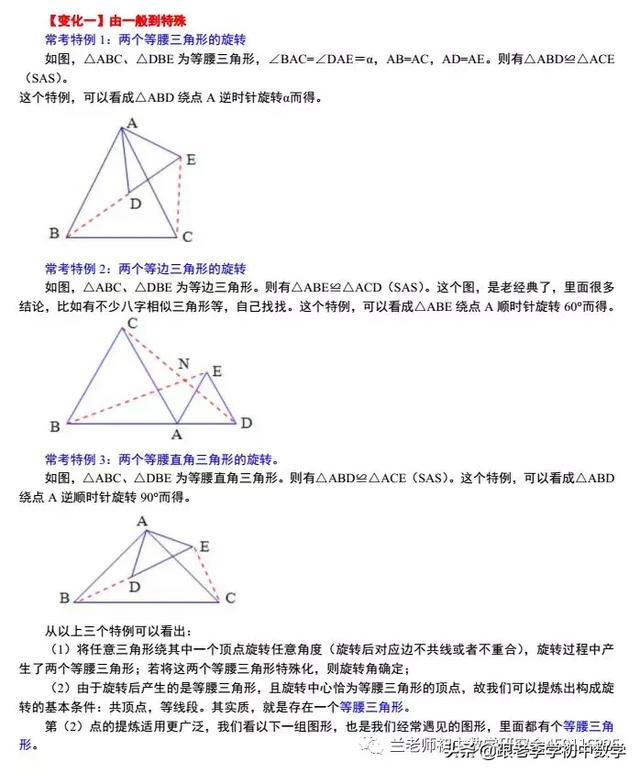
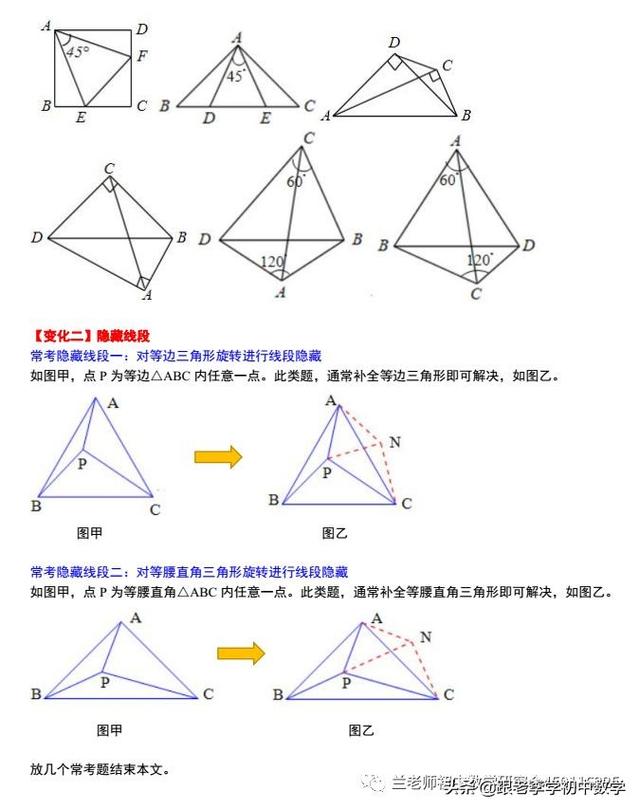
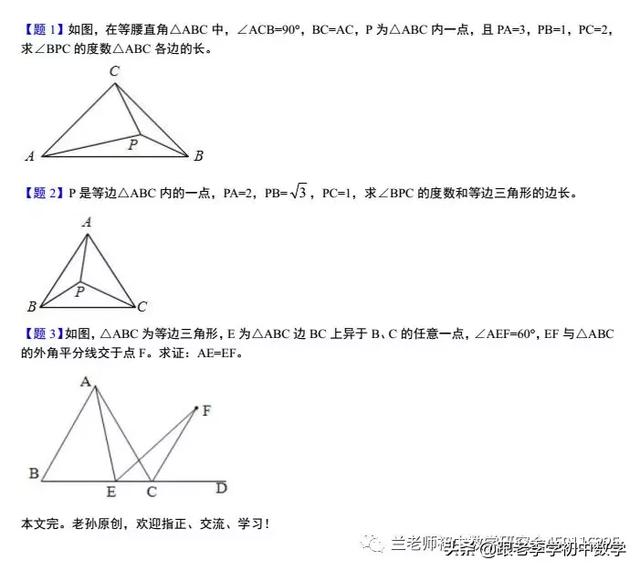
如图，△ABC和三角形ADE为等腰直角三角形，△ABC固定不动，△ADE绕顶点A顺时针旋转。不难想象，△ADE的顶点旋转轨迹如图乙所示：D、E始终在在以点A为圆心、AD长为半径的圆上，且长度不变。

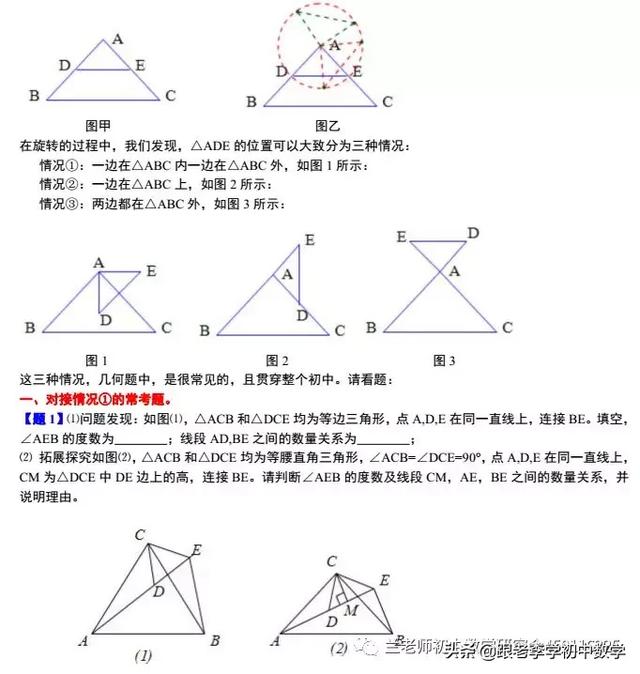
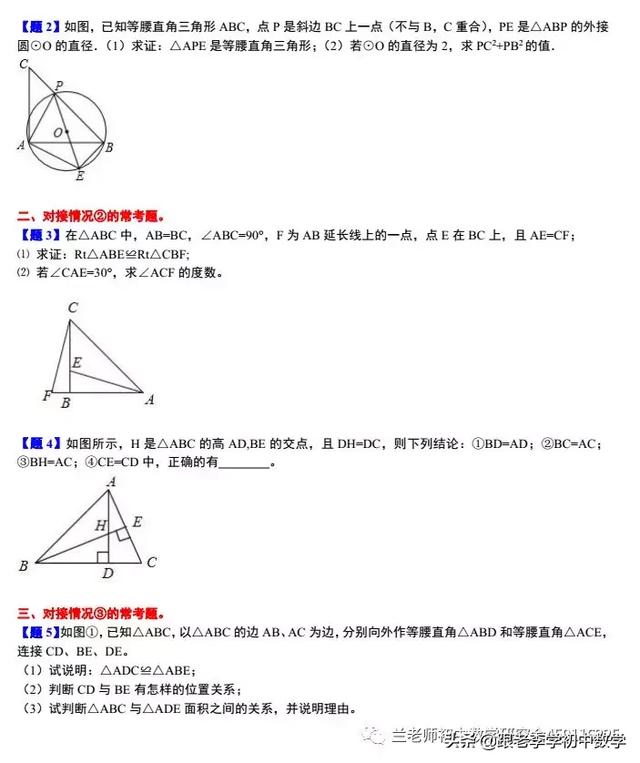
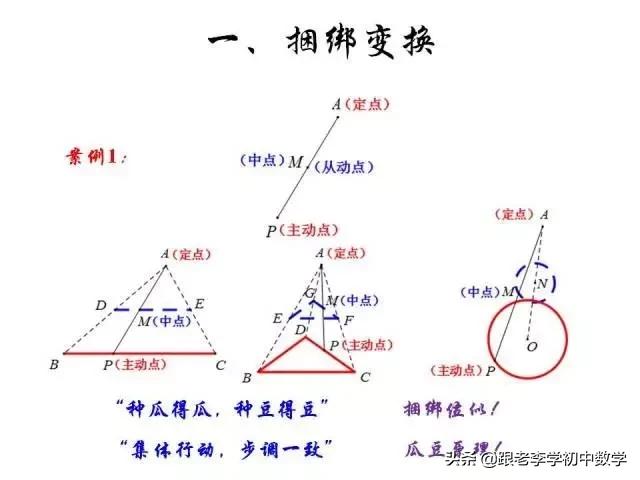
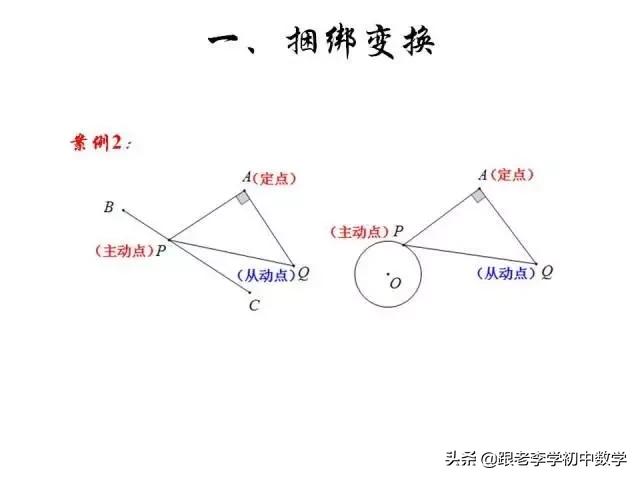
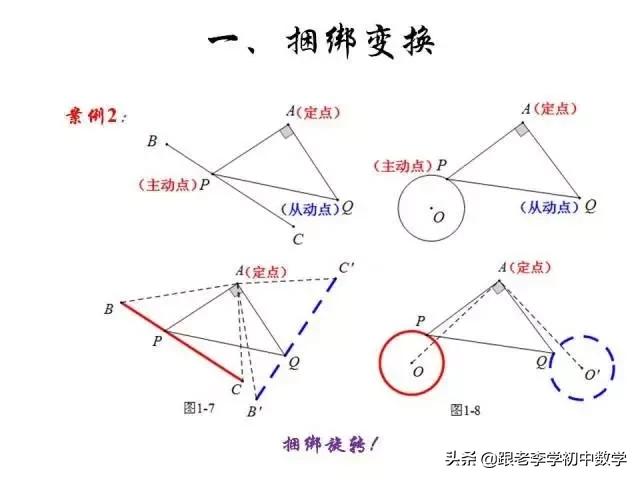
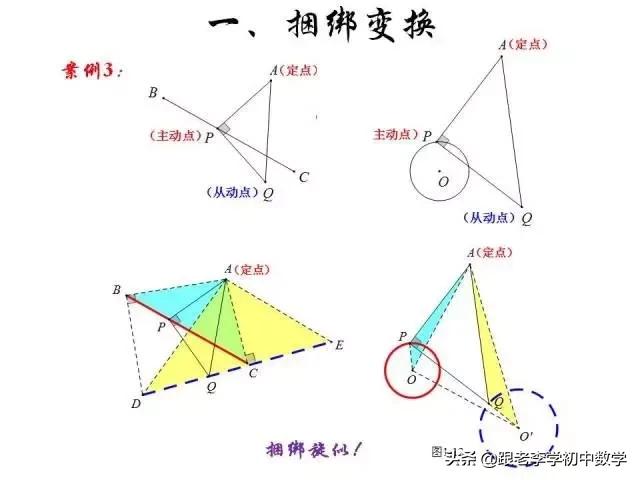
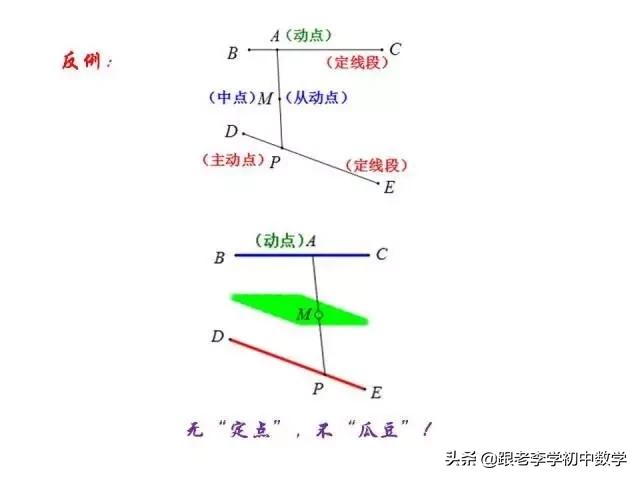
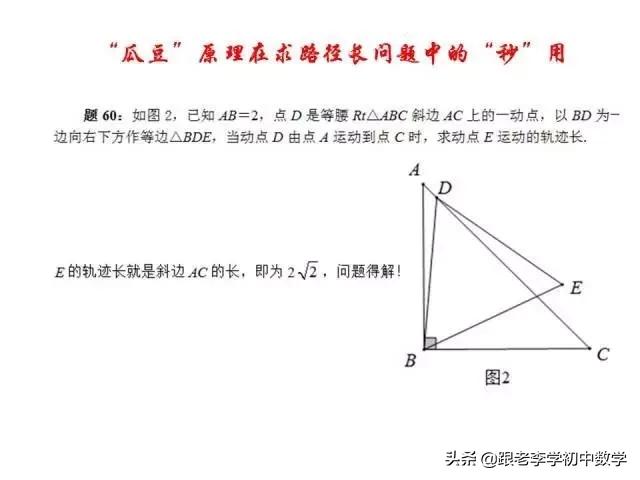
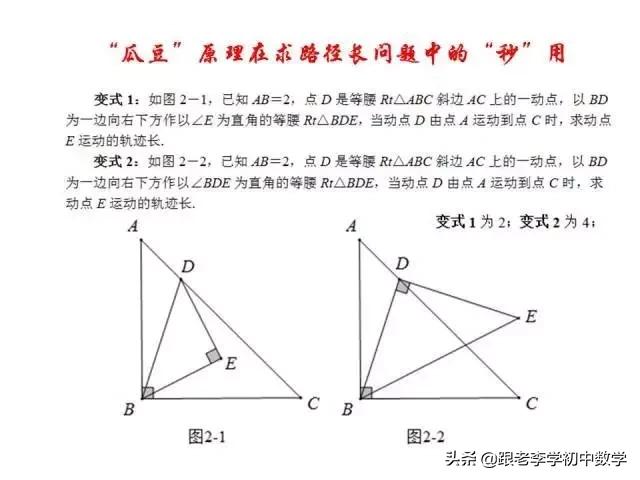
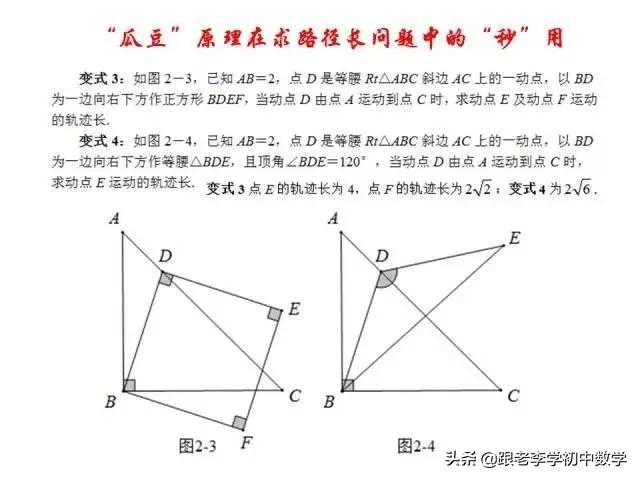
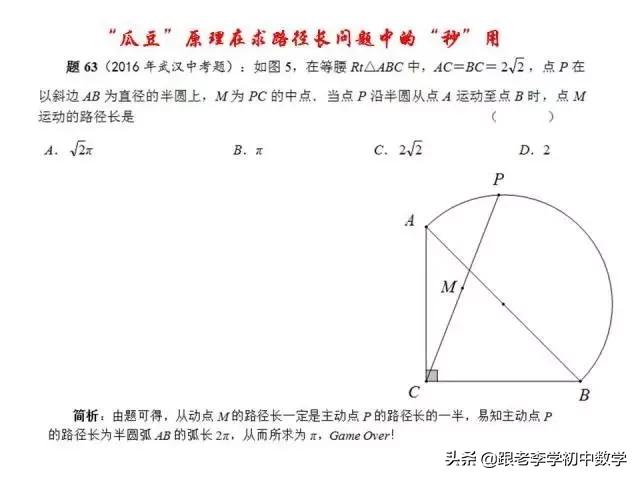
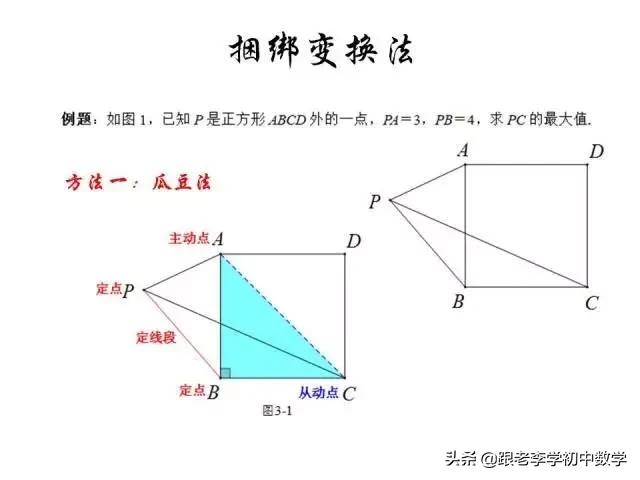
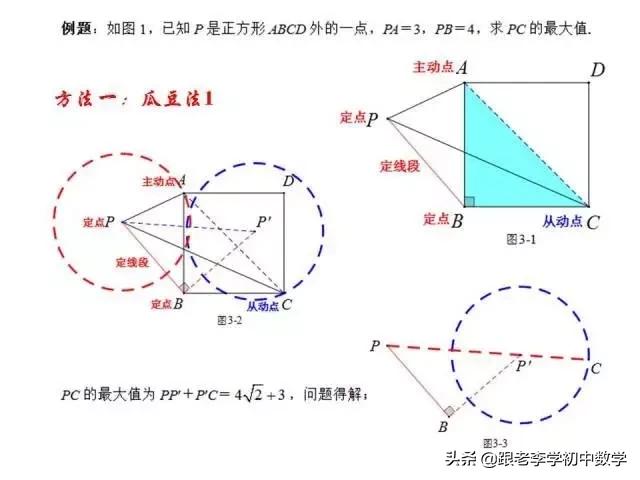
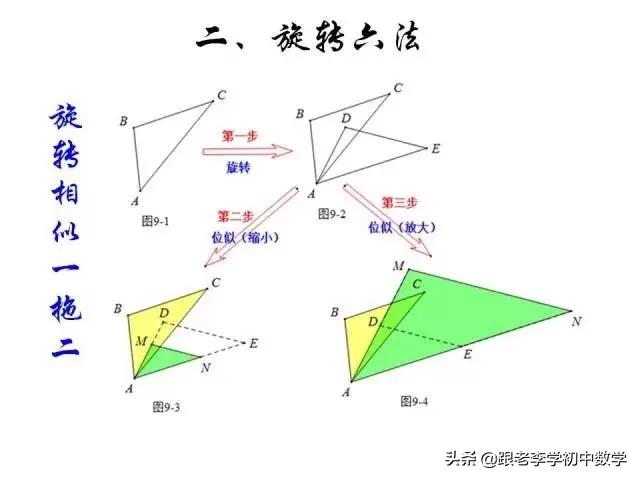
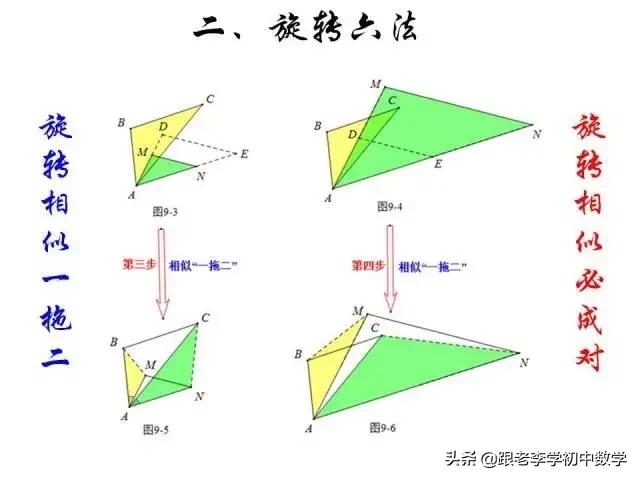
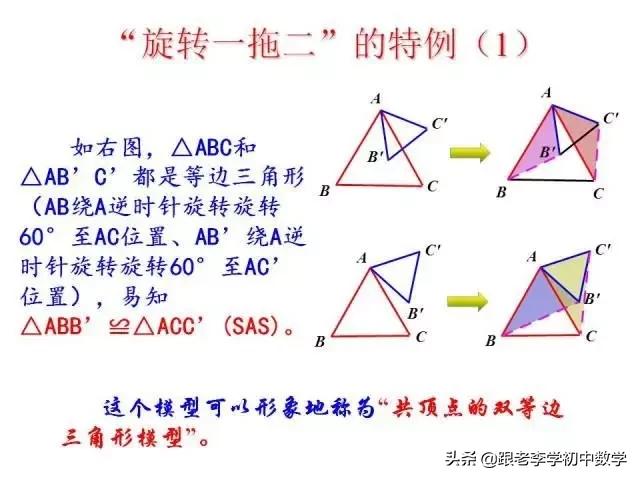
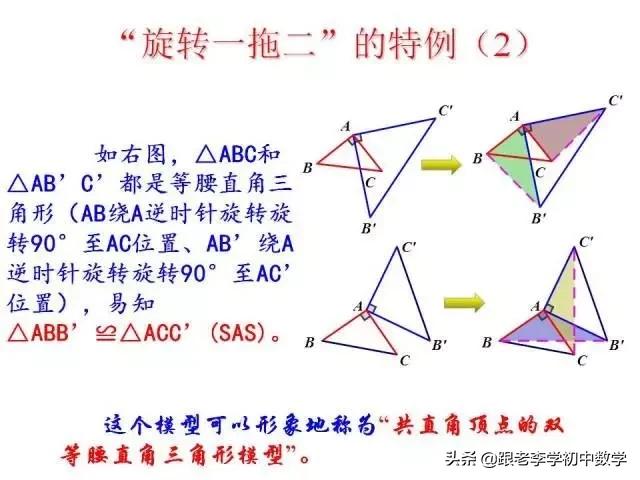
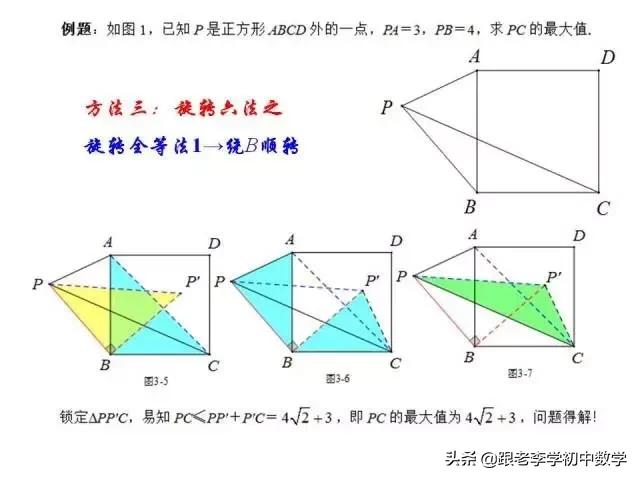
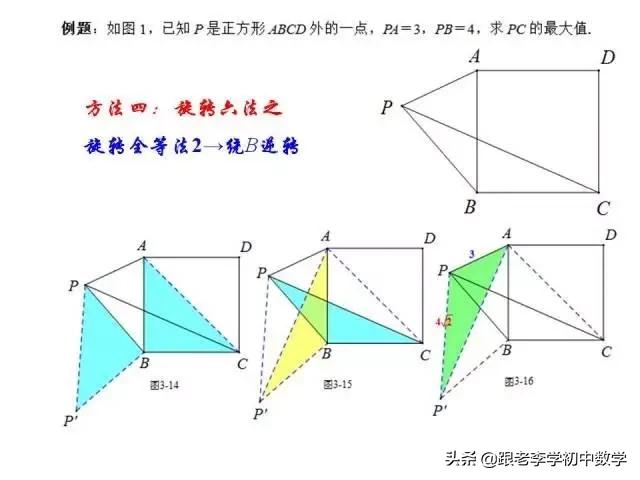
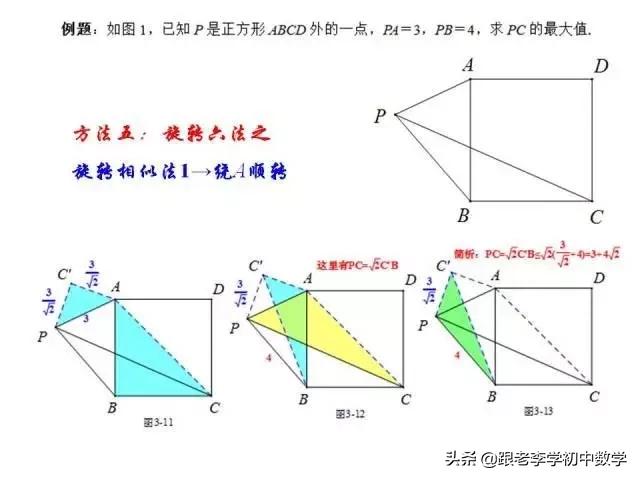
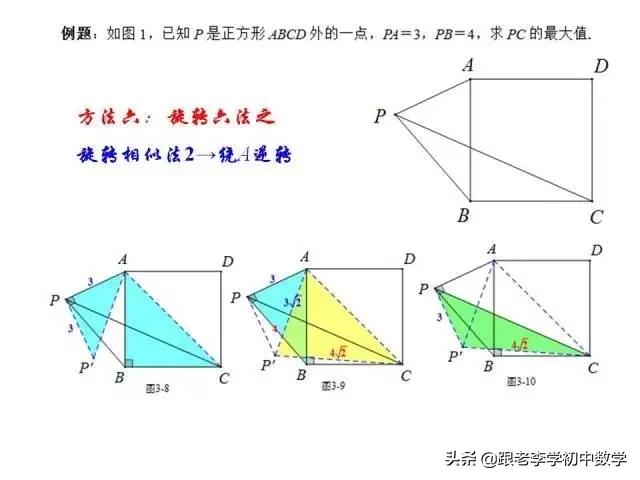
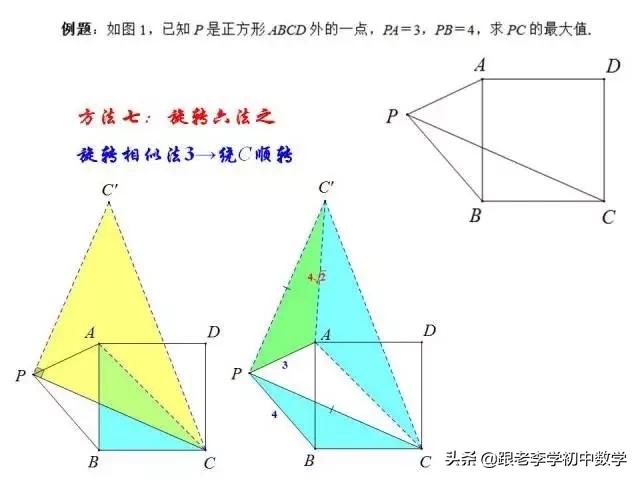
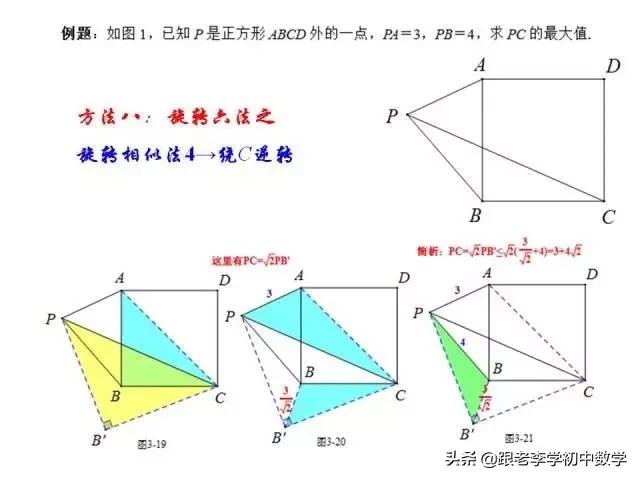
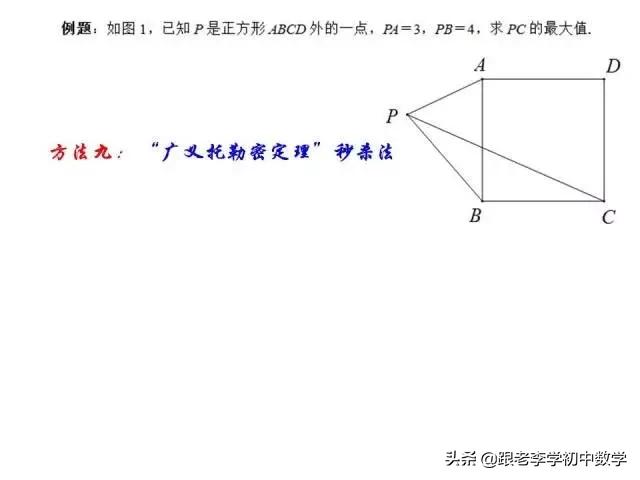
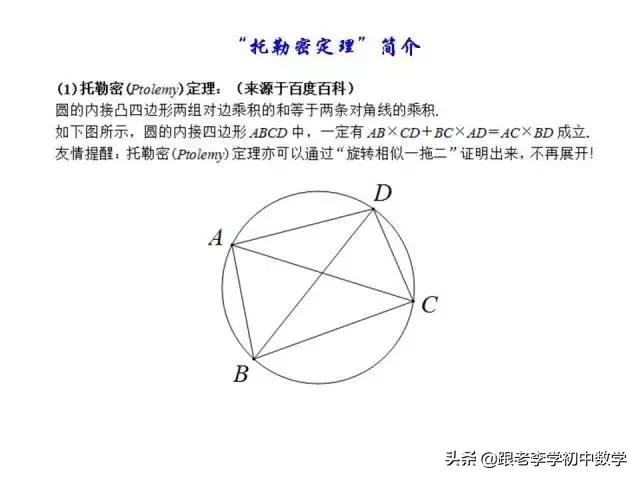
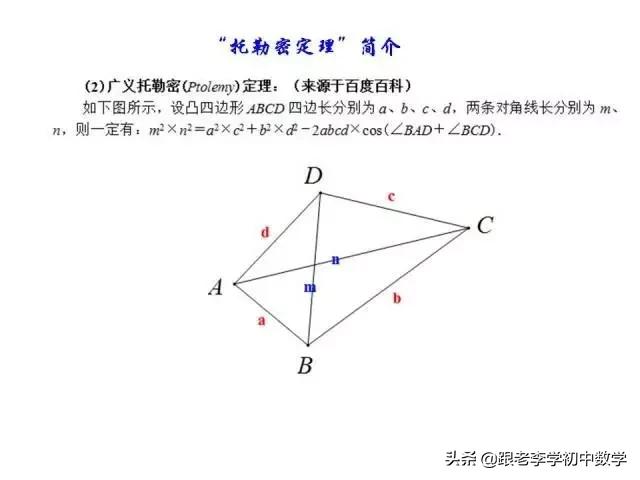
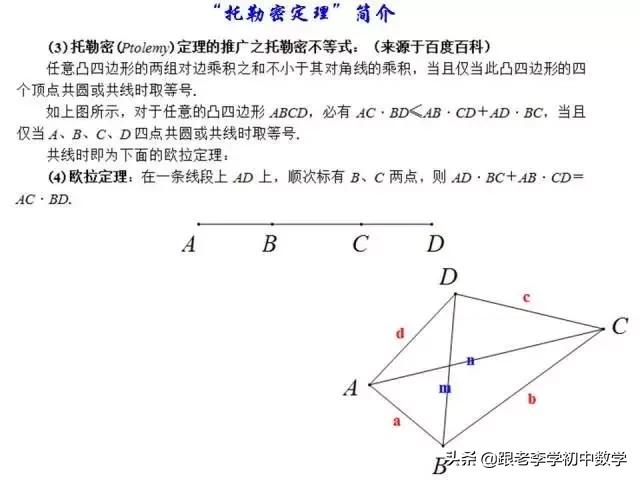
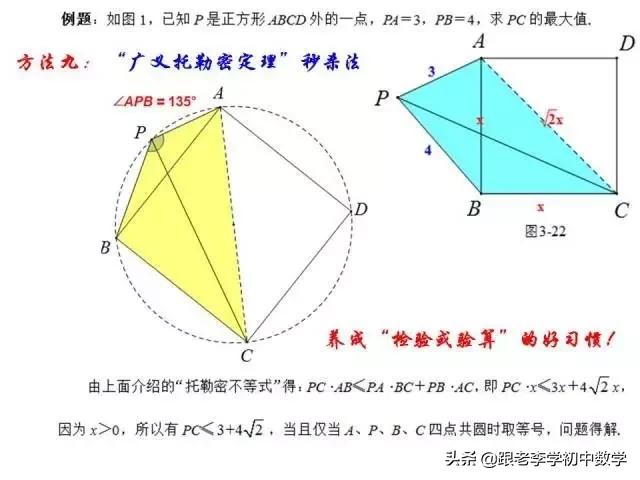
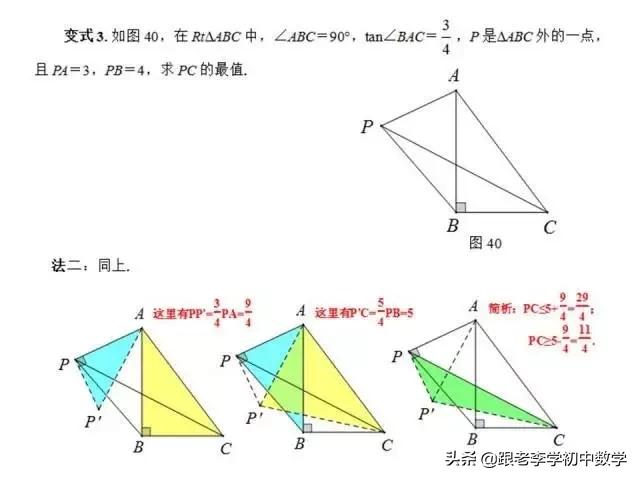
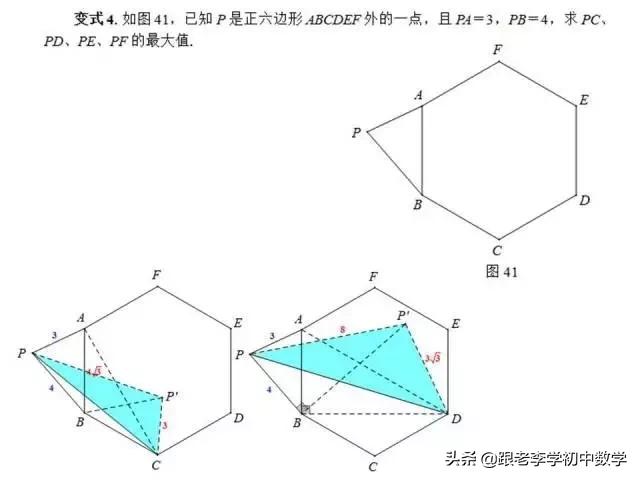
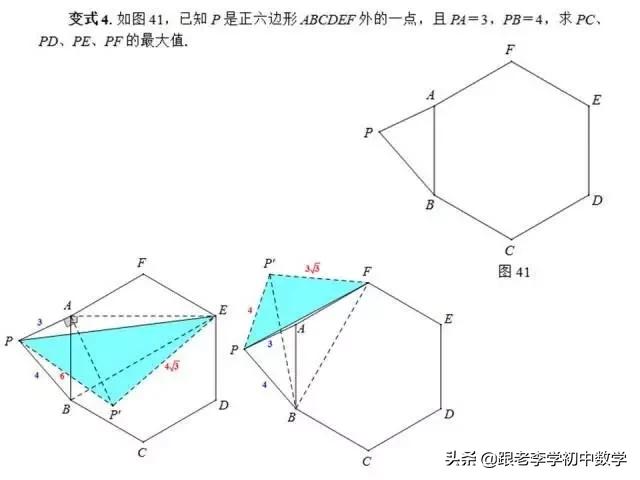
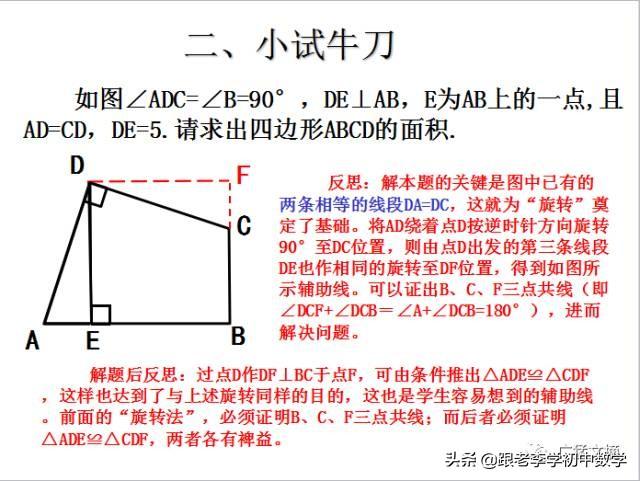
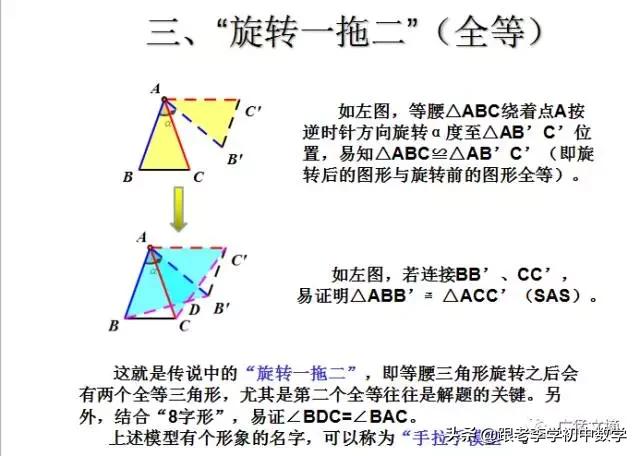
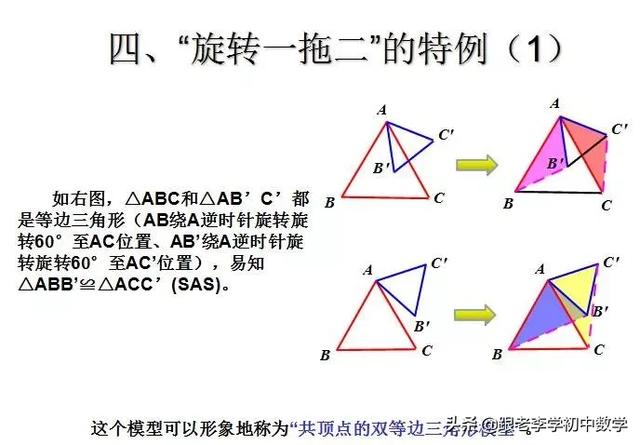
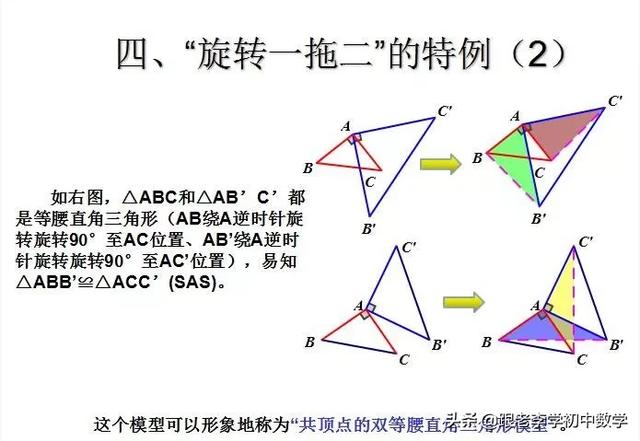
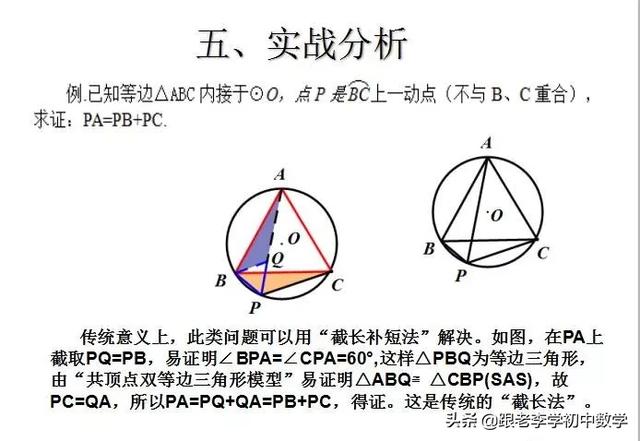
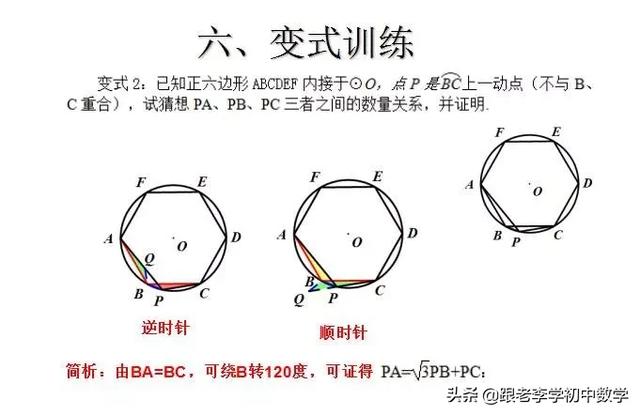
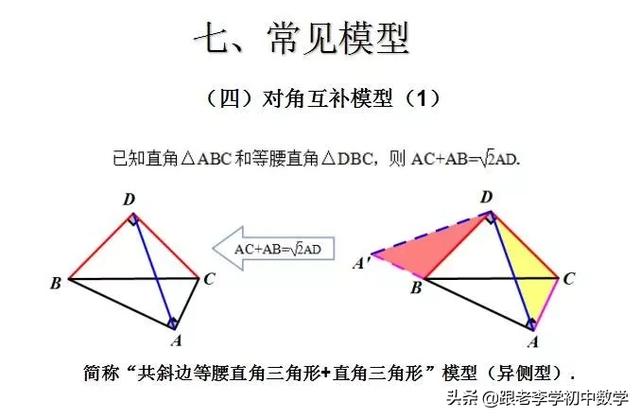
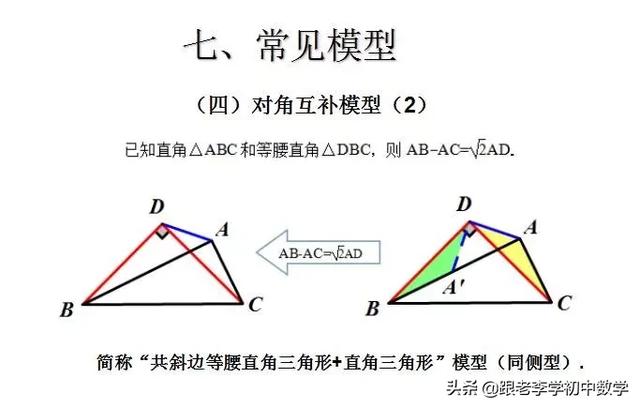
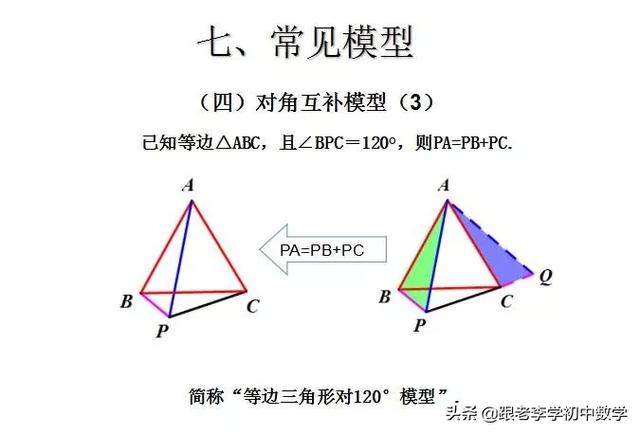
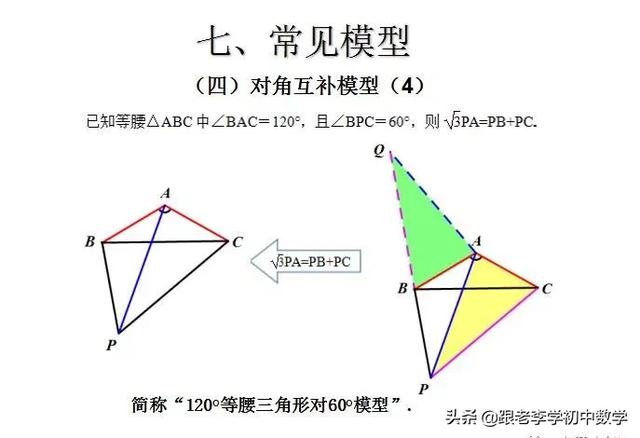
这一部分重点讲述有关“旋转”的一些常见的基本图形，用旋转法“一统”各种模型，使学生真正走进这些模型中里，以期学生在复杂的图形中识别或者构造这些基本图形，达到真正“通”之地步！

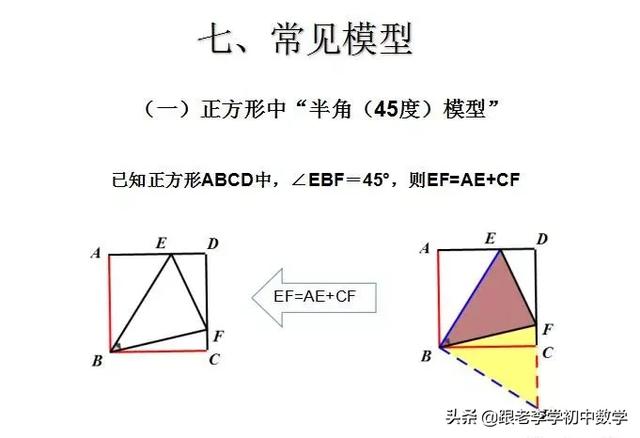
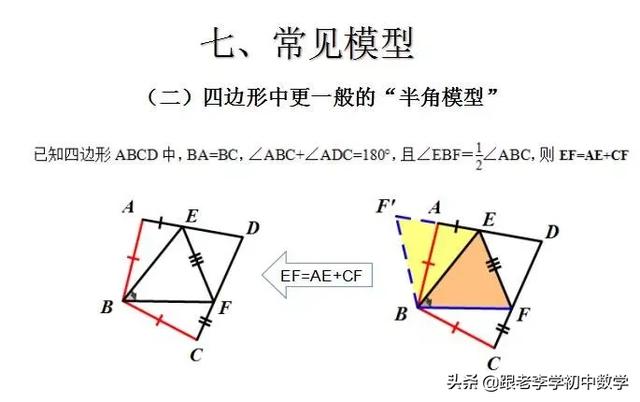
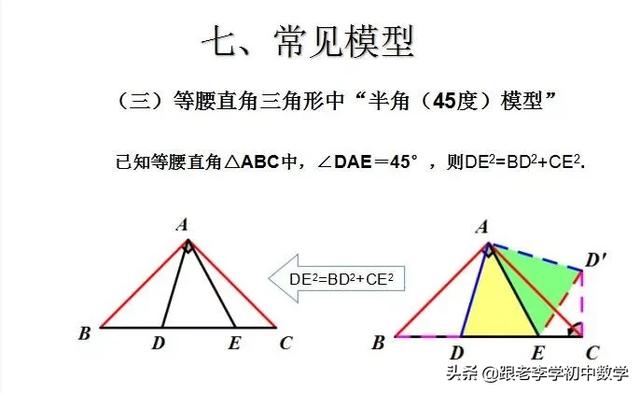
广告

一题一课.初中数学好题赏析

作者：刘彦永