MATLAB实现的势场法路径规划详尽教程

本文还有配套的精品资源，点击获取

简介：势场法路径规划是一种模拟物理力场原理，用于为移动机器人或无人车辆在复杂环境中寻找最优路径的技术。本MATLAB程序详细注解了实现过程，包括环境建模、势场构建、力场计算、路径搜索和优化等关键步骤。该程序不仅帮助理解势场法的基本原理和实现细节，还提升了MATLAB编程和数值计算能力，对多个领域具有应用价值。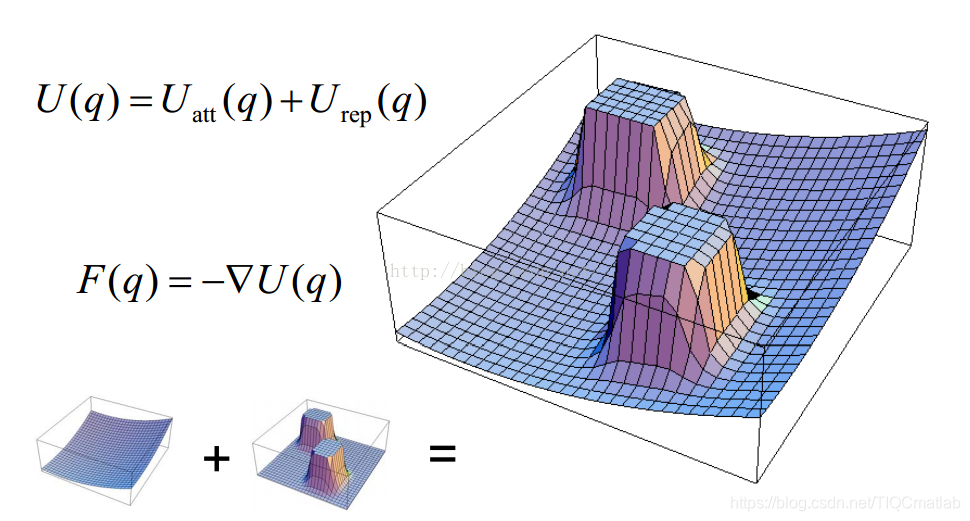

1. 势场法路径规划概述

1.1 势场法路径规划简介

势场法路径规划是一种在机器人导航和动态环境中寻找路径的常用技术。它依赖于构建势场环境，通过算法计算从起点到终点的最优路径，同时避免障碍物和潜在的陷阱。

1.2 势场法的起源与发展

最早由Khatib在1986年提出，势场法被广泛应用于移动机器人的路径规划领域。它通过模拟物理势场，如电场或重力场，将环境中的障碍物映射为斥力场，目标位置映射为引力场，机器人的路径规划则转化为寻求这两力场的平衡点。

1.3 势场法的应用领域

势场法路径规划不仅用于机器人领域，还扩展到无人机导航、自动驾驶汽车、虚拟现实、游戏开发等多个高技术领域。其核心优势在于直观的物理模型和相对简单的实现过程。

graph LR
    A[环境分析] --> B[势场构建]
    B --> C[力场计算]
    C --> D[路径搜索]
    D --> E[路径优化]
    E --> F[最终路径生成]

在上述流程中，环境分析是初步理解操作空间的过程。随后进行势场构建，包括引力场和斥力场的模型设计。之后，通过力场计算来确定每一位置的势能，进而搜索出路径。路径优化考虑避开局部最小值，优化路径平滑度，最后生成可执行的路径。上述流程可用Mermaid代码块来表示一个流程图，便于理解势场法路径规划的整体流程。

2. MATLAB环境搭建与基础操作

2.1 MATLAB软件环境介绍

2.1.1 MATLAB软件的安装与配置

MATLAB（Matrix Laboratory的缩写）是由MathWorks公司开发的一款高性能数值计算和可视化软件。它广泛应用于工程计算、算法开发、数据分析和可视化等领域。MATLAB的安装过程是相对简单的，但关键在于如何配置好环境以便能够充分发挥其功能。

首先，前往MathWorks官方网站下载MATLAB的安装包。下载完成后，双击安装文件开始安装过程。在此过程中，系统会引导用户选择安装的组件，其中包含核心MATLAB软件、工具箱（Toolboxes）、Simulink等。根据您的专业需求和个人兴趣，选择相应的工具箱进行安装。

安装完成后，需要进行环境配置。这包括设置MATLAB的路径，使其能够识别到安装的工具箱和自定义的脚本文件。可以通过MATLAB的界面，点击"Home"标签页下的"Set Path"按钮来管理路径。也可以在MATLAB命令窗口中使用 addpath 函数来动态添加路径。

2.1.2 MATLAB工作空间与工具箱概述

MATLAB的工作空间是用户在MATLAB环境中进行交互和编程的区域。在此区域中，用户可以创建和操作变量、执行函数调用，以及运行脚本和函数。工作空间中的内容可以通过 who 或 whos 命令查看，使用 clear 命令可以清除工作空间中的变量。

工具箱（Toolboxes）是MATLAB中专门针对某一领域开发的附加软件包。例如，Robotics Toolbox用于机器人运动学与动力学的分析和仿真，Image Processing Toolbox用于图像处理，Signal Processing Toolbox用于信号处理。每个工具箱都包含了一系列功能强大的函数和应用程序，极大地扩展了MATLAB的核心能力。

2.2 MATLAB编程基础

2.2.1 MATLAB基本语法结构

MATLAB的基本语法结构非常直观。它是一种矩阵导向的语言，所有的变量默认为矩阵（或数组）。以下是一些MATLAB的基本语法结构：

• 变量赋值：使用 = 进行赋值操作，例如 a = 5;
• 矩阵创建：使用方括号 [] 创建矩阵，例如 A = [1 2; 3 4];
• 数学运算：支持多种数学运算，如加法 + 、减法 - 、乘法 * 、除法 / ，以及点运算符（如 .^ 用于数组的元素对元素乘方）。
• 函数调用：通过输入函数名称和参数，例如 sin(0.5) 。
• 控制语句：包括 if 条件语句、 for 循环和 while 循环等。

2.2.2 矩阵操作与数组计算

MATLAB中最强大的功能之一是它的矩阵操作能力。例如，矩阵加法、乘法可以直接使用运算符进行：

A = [1 2; 3 4];
B = [5 6; 7 8];

C = A + B;  % 矩阵加法
D = A * B;  % 矩阵乘法

此外，MATLAB还支持矩阵的转置（使用单引号 ' ）、矩阵求逆（使用 inv 函数）等高级操作。这些操作让MATLAB在进行线性代数计算时显得游刃有余。

数组计算方面，MATLAB支持数组运算，允许直接对数组进行元素级别的操作，而不需要显式的循环语句。这在处理大规模数据集时显得特别高效。

2.2.3 图形用户界面（GUI）操作指南

MATLAB提供了一套图形用户界面（GUI）设计工具，使得用户可以不需要编写代码，通过拖放控件来设计交互式GUI应用程序。通过 guide 或 appdesigner 命令可以打开GUI设计环境。

GUI设计的关键在于布局控件、设置控件属性以及编写回调函数。回调函数是指用户在界面上进行操作（如点击按钮）时，MATLAB触发并执行的代码。以下是一个简单的GUI设计示例：

uicontrol('Style', 'pushbutton', 'String', 'Click Me', ...
          'Position', [***], 'Callback', @myCallback);

function myCallback(src, event)
    disp('Button clicked');
end

在上述示例中，创建了一个按钮控件，并为该按钮指定了一个回调函数 myCallback ，当按钮被点击时，控制台会显示"Button clicked"消息。

MATLAB的GUI功能允许非编程用户也能够创建强大的交互式应用程序，极大地拓宽了MATLAB的应用场景。

在继续深入学习MATLAB和势场法之前，一个良好的软件环境是必不可少的。通过本章的介绍，您应该已经具备了MATLAB环境搭建和基本操作的能力，为后续章节的深入学习打下了坚实的基础。在下一章中，我们将探索势场法理论基础和构建方法，以及如何在MATLAB中实现势场计算与路径生成。

3. 势场法建模与计算机制

3.1 势场法理论基础

势场法是一种将机器人运动规划问题转换为寻找势能场最小能量路径的优化问题的方法。势场法由Khatib于1986年提出，它基于物理学中的势能理论，将机器人的运动环境抽象成一个虚拟的势场，其中障碍物生成一个排斥势场，目标位置则生成一个吸引势场。

3.1.1 势场法基本概念与原理

势场法的基本原理是将机器人视为一个质点，通过计算质点在势场中的运动方程来规划其运动轨迹。机器人受到的势能由障碍物产生的排斥势能和目标产生的吸引势能组成。势场法的关键在于构建合理的势场函数，这要求势场具有以下特性：目标位置的吸引势场能够引导机器人移动到目标点，障碍物周围的排斥势场能够避免机器人碰撞障碍物。

3.1.2 势场与力场的关系

在势场法中，势场和力场是相互关联的。势场表示了系统中势能的分布，而力场则是势场的空间导数，表示了势能随位置变化产生的力。具体来说，力场是势场函数的负梯度。因此，通过计算势场的梯度，我们可以得到作用在机器人上的力，进而求解机器人的运动方程。

3.2 势场构建与数值计算

构建准确的势场模型是势场法成功应用的关键。势场的构建涉及到对环境的精确建模以及对势场函数的有效选择。

3.2.1 势场构建过程详解

势场构建通常包括以下几个步骤： 1. 环境建模：根据实际应用场景，获取环境地图，并将障碍物位置明确地标定出来。 2. 势场函数选择：选择合适的势场函数来表示吸引势场和排斥势场。常见的吸引势场函数形式有引力势能模型，排斥势场则通常使用斥力势能模型。 3. 参数设定：为势场函数设定适当的参数，这些参数决定了势场的分布特性，如力的强度和作用范围。 4. 势场合成：通过合成吸引势场和排斥势场，得到完整的势场分布图。

3.2.2 势场计算的数值方法

势场的计算需要借助数值方法进行，常见的数值计算方法包括有限差分法和有限元法。以下以有限差分法为例：

假设势场函数 ( U(x, y) ) 表示二维空间中的势能分布，那么势场 ( F(x, y) ) 可以通过计算 ( U(x, y) ) 在空间中的梯度获得：

% 假设 U 是势场函数
[Ux, Uy] = gradient(U, deltax, deltay);
F = -sqrt(Ux.^2 + Uy.^2);

在上述代码中， gradient 函数用于计算函数 ( U ) 在 ( x ) 和 ( y ) 方向上的梯度， deltax 和 deltay 表示空间步长。

3.2.3 势场函数的实现技巧

势场函数的实现需要考虑以下因素：

• 吸引势场 ：确保机器人能够被目标位置吸引，通常采用随距离增加而减少的势场函数。
• 排斥势场 ：在障碍物附近提供足够大的斥力，阻止机器人进入障碍区域。通常使用随距离减小而迅速增大的势场函数。
• 平滑过渡 ：势场在吸引和排斥区域之间应平滑过渡，以避免在路径上产生“震荡”，影响路径质量。

实现势场函数时，可能需要进行多次试验和调整以获得最佳性能。此外，势场函数应能够适应不同形状和大小的障碍物，并且在多障碍物环境中能够稳定工作。以下是MATLAB代码示例，展示如何实现一个基本的势场函数：

% 定义势场函数
function U = potential_field_function(x, y, goal, obstacle)
    % 参数：坐标点(x, y)，目标位置goal，障碍物位置obstacle
    % 计算到目标点的距离
    r_goal = sqrt((x-goal(1)).^2 + (y-goal(2)).^2);
    % 计算到障碍物的距离
    r_obstacle = sqrt((x-obstacle(1)).^2 + (y-obstacle(2)).^2);
    % 吸引势场函数
    U_goal = -1 / r_goal;
    % 排斥势场函数
    U_obstacle = 1 / r_obstacle;
    % 合成势场函数
    U = U_goal - U_obstacle;
end

在该函数中，机器人会受到目标位置的吸引势场和障碍物的排斥势场的共同作用。通过调整 ( U_goal ) 和 ( U_obstacle ) 的参数，可以对势场进行微调，以适应不同的规划环境和要求。

4. 力场计算与路径生成

4.1 力场计算理论

4.1.1 力场计算的基本公式

力场计算是路径规划中的核心过程，它依赖于势场法的基本公式和理论模型。在一个二维空间内，力场的计算可以通过以下公式来描述：

[ F(x, y) = -\nabla V(x, y) ]

其中 ( F(x, y) ) 表示在空间位置 (x, y) 处的力场值，( \nabla ) 表示梯度运算符，而 ( V(x, y) ) 是势场函数。势场函数通常由目标势场、障碍物势场和任何其他可能影响路径的额外势场组成。

4.1.2 力场中的梯度计算

梯度是一个向量运算，它给出了函数在某一点处的最大变化率及其方向。对于连续可导的势场函数 ( V(x, y) )，梯度可以用偏导数来计算：

[ \nabla V(x, y) = \left( \frac{\partial V}{\partial x}, \frac{\partial V}{\partial y} \right)^T ]

在实际编程实现中，梯度的计算通常使用差分方法近似，例如：

function [Fx, Fy] = calculateGradient(V, x, y)
    h = 1e-5; % 微分步长
    Fx = (V(x+h, y) - V(x-h, y)) / (2*h);
    Fy = (V(x, y+h) - V(x, y-h)) / (2*h);
end

4.2 路径搜索与生成

4.2.1 基于势场法的路径搜索策略

在路径搜索策略中，机器人或移动体被视为质点，它会受到势场的影响而沿着力场的负梯度方向移动。路径搜索策略的关键在于选择合适的步长，以及如何处理障碍物和局部最小值问题。一个简单的策略是：

function path = searchPath(startPoint, goalPoint)
    % 初始化路径数组
    path = [startPoint];
    while距离(path(end), goalPoint) > 容许误差
        % 计算当前位置的势场和梯度
        [V, Fx, Fy] = evaluatePotentialField(path(end));
        % 更新位置
        path(end+1) = path(end) + 步长 * [-Fx, -Fy];
        % 检查是否遇到障碍物
        if遇到障碍物(path(end+1))
            path(end+1) = backStep(path);
        end
    end
end

4.2.2 路径生成的具体实现步骤

路径生成步骤包括初始化路径点、计算每个点的力场、更新位置，直到达到目标位置或路径长度超过预设值。下面是一个简化的路径生成示例代码：

% 初始化参数和路径数组
startPoint = [x0, y0];
goalPoint = [xg, yg];
path = [startPoint];
currentPoint = startPoint;
while 距离(currentPoint, goalPoint) > 容许误差
    % 计算势场
    [V, Fx, Fy] = calculatePotential(currentPoint);
    % 更新位置
    currentPoint(1) = currentPoint(1) - 步长 * Fx;
    currentPoint(2) = currentPoint(2) - 步长 * Fy;
    % 检查边界条件
    if currentPoint(1) < x_min || currentPoint(1) > x_max || ...
       currentPoint(2) < y_min || currentPoint(2) > y_max
       break; % 跳出循环
    end
    % 更新路径数组
    path = [path; currentPoint];
end

4.2.3 路径生成的优化与调整

路径生成的优化和调整主要集中在减少计算复杂度、提高路径质量以及处理特殊情况（如局部最小值）。可以采用如下方法：

• 自适应步长调整：基于路径点的势场强度动态调整步长，势场强时减小步长，弱时增大。
• 动态势场调整：在势场计算中引入动态权重调整机制，当检测到局部最小值附近时增加权重，以避免陷入。
• 后处理优化：使用诸如贝塞尔曲线、样条插值等数学方法对生成路径进行平滑处理。

表格

以下是几种常见的路径生成策略对比表格：

| 策略名称 | 步长策略 | 障碍物处理 | 适用场景 | | ------------ | -------------- | ---------- | ---------------- | | 固定步长法 | 预设步长 | 忽略 | 障碍物简单且稀疏 | | 动态步长法 | 势场动态调整 | 忽略 | 障碍物复杂但稀疏 | | 反向步进法 | 固定步长 | 有效 | 障碍物密集且复杂 | | 路径平滑算法 | 固定或动态步长 | 忽略 | 后处理优化 |

mermaid 流程图

以下是基于势场法的路径生成流程图：

graph LR
    A[开始] --> B[初始化路径点]
    B --> C[计算当前点势场]
    C --> D[根据势场更新位置]
    D --> E{是否达到目标}
    E -- 是 --> F[路径完成]
    E -- 否 --> C

代码块

% 模拟路径生成的MATLAB代码
currentPoint = [1, 1]; % 初始位置
goalPoint = [10, 10]; % 目标位置
path = [currentPoint]; % 初始化路径数组

while norm(currentPoint - goalPoint) > 0.01
    % 计算当前位置势场梯度
    grad = gradientPotentialField(currentPoint);
    % 更新当前位置
    currentPoint = currentPoint - 0.1 * grad;
    % 保持路径点在设定范围内
    currentPoint(1) = max(min(currentPoint(1), 10), 1);
    currentPoint(2) = max(min(currentPoint(2), 10), 1);
    % 更新路径数组
    path = [path; currentPoint];
end

在上述MATLAB代码中， gradientPotentialField 函数用于计算给定点的势场梯度， norm 函数用于计算向量的模，确保路径点在设定的范围之内，防止移动超出边界。这段代码为路径生成的基础实现，可以通过调整步长和梯度计算方法来提高路径的生成质量。

5. 路径优化与平滑处理

在实际的路径规划应用中，简单的路径搜索算法往往不能满足复杂的实际需求。为了提高路径的质量和适应性，路径优化与平滑处理显得尤为重要。路径优化可以提升路径的效率和安全性，而平滑处理则可以确保路径的连贯性和可执行性。

5.1 路径优化的必要性

5.1.1 优化路径的目标与方法

路径优化的目的是生成一条满足特定要求的路径，这些要求通常包括最短路径、最小化转弯、最少的能量消耗等。路径优化通常采用启发式算法，如遗传算法、粒子群优化、蚁群算法等，这些算法能够在广阔的搜索空间中找到接近最优解的路径。

例如，蚁群算法通过模拟蚂蚁寻找食物的行为，使用信息素更新机制来引导路径搜索，最终收敛于最优或近似最优解。代码示例展示了如何使用蚁群算法进行路径优化：

import numpy as np

class AntColonyOptimizer:
    def __init__(self, distances, n_ants, n_best, n_iterations, decay, alpha=1, beta=1):
        """
        Ant colony optimizer for the traveling salesman problem.
        Args:
        - distances: 2D numpy.array of distances. The diagonal should be numpy.inf.
        - n_ants: Number of ants running per iteration
        - n_best: Number of best ants who deposit pheromone
        - n_iterations: Number of iterations
        - decay: Rate it which pheromone decays. The pheromone value is multiplied by decay, so 0.95 will lead to decay, 0.5 to much faster decay.
        - alpha: exponenet on pheromone, higher alpha give pheromone more weight. Default=1
        - beta: exponenet on distance, higher beta give distance more weight. Default=1
        """
        self.distances = distances
        self.pheromone = np.ones(self.distances.shape) / len(distances)
        self.all_inds = range(len(distances))
        self.n_ants = n_ants
        self.n_best = n_best
        self.n_iterations = n_iterations
        self.decay = decay
        self.alpha = alpha
        self.beta = beta

    def run(self):
        shortest_path = None
        all_time_shortest_path = ("placeholder", np.inf)
        for _ in range(self.n_iterations):
            all_paths = self.gen_all_paths()
            self.spread_pheromone(all_paths, self.n_best, shortest_path=shortest_path)
            shortest_path = min(all_paths, key=lambda x: x[1])
            if shortest_path[1] < all_time_shortest_path[1]:
                all_time_shortest_path = shortest_path            
            self.pheromone * self.decay
        return all_time_shortest_path

    def spread_pheromone(self, all_paths, n_best, shortest_path):
        sorted_paths = sorted(all_paths, key=lambda x: x[1])
        for path, dist in sorted_paths[:n_best]:
            for move in path:
                self.pheromone[move] += 1.0 / self.distances[move]

    def gen_path_dist(self, path):
        total_dist = 0
        for ele in path:
            total_dist += self.distances[ele]
        return total_dist

    def gen_all_paths(self):
        all_paths = []
        for _ in range(self.n_ants):
            path = self.gen_path(0)
            all_paths.append((path, self.gen_path_dist(path)))
        return all_paths

    def gen_path(self, start):
        path = []
        visited = set()
        visited.add(start)
        prev = start
        for _ in range(len(self.distances) - 1):
            move = self.pick_move(self.pheromone[prev], self.distances[prev], visited)
            path.append((prev, move))
            prev = move
            visited.add(move)
        path.append((prev, start)) # return to start
        return path

    def pick_move(self, pheromone, dist, visited):
        pheromone = np.copy(pheromone)
        pheromone[list(visited)] = 0

        row = pheromone ** self.alpha * (( 1.0 / dist) ** self.beta)
        norm_row = row / row.sum()
        move = np_choice(self.all_inds, 1, p=norm_row)[0]
        return move

def np_choice(a, size, p):
    return np.random.choice(a, size=size, replace=False, p=p)

# 假设距离矩阵是一个上三角矩阵
distances = np.triu(np.random.rand(10,10)) * 100
distances = (distances + distances.T) / 2  # Make it symmetric
np.fill_diagonal(distances, np.inf)  # No self loops

# 初始化蚁群优化器
ac = AntColonyOptimizer(distances=distances,
                        n_ants=10,
                        n_best=5,
                        n_iterations=100,
                        decay=0.95,
                        alpha=1,
                        beta=2)
shortest_path = ac.run()
print("Shortest path: {}".format(shortest_path))

上述代码定义了一个蚁群优化器类，并用它来解决旅行推销员问题。代码中展示了初始化蚁群优化器、运行优化算法、路径生成和信息素更新等过程。通过参数的调整，可以对算法的性能进行优化。

5.1.2 路径平滑的基本概念

路径平滑指的是通过数学方法对原始路径进行处理，以消除路径中的尖锐转折和突变，使得路径更加平滑。平滑后的路径不仅视觉上更加自然，而且降低了机器人或车辆的控制难度，提高了行驶安全性。

5.2 路径优化技术

5.2.1 常见的路径优化算法

除了蚁群算法，还有许多其他路径优化算法，例如模拟退火算法、遗传算法和A*算法的变种。这些算法各有特点，在不同的应用场合有不同的表现。

5.2.2 平滑处理的方法与技巧

路径平滑处理的方法通常涉及到数学优化问题，可以采用多项式拟合、贝塞尔曲线拟合等方法来平滑路径。例如，利用贝塞尔曲线拟合路径时，可以通过调整控制点的位置来获得平滑的路径。

import matplotlib.pyplot as plt
from scipy.special import comb

def factorial(n):
    return np.prod(np.arange(1, n + 1))

def bernstein_poly(i, n, t):
    return comb(n, i) * (t**(n - i)) * (1 - t)**i

def generate_bernstein_points(n):
    return [bernstein_poly(i, n, t) for i in range(n + 1)]

def bezier_curve控制点, t):
    n = len(控制点) - 1
    return sum(bernstein_poly(i, n, t) * P[i] for i in range(len(控制点))) for P in 控制点.T]

# 定义一些路径控制点
控制点 = np.array([(0, 0), (2, 3), (3, 4), (4, 0), (5, 5), (6, 0)])

# 计算贝塞尔曲线
t_values = np.linspace(0, 1, 100)
path = [bezier_curve(控制点, t) for t in t_values]

# 绘制贝塞尔曲线路径
plt.plot([p[0] for p in path], [p[1] for p in path], label="Bezier Curve")

plt.legend()
plt.show()

在上述代码中，通过使用贝塞尔曲线来生成平滑的路径。控制点的调整是关键，它决定了最终路径的形状和光滑程度。调整控制点的位置，可以实现路径的精细控制。

路径优化与平滑处理的策略不仅仅局限于上述方法。它们需要根据实际应用场景的特定需求进行调整和定制，以达到最佳的优化效果。在接下来的章节中，我们将介绍如何结合全局路径规划进一步提升势场法的性能。

6. 解决势场法局部最小值问题

势场法在路径规划中是一个强有力的工具，但它的应用也面临挑战，其中之一就是局部最小值问题。局部最小值是指在势场中存在一些点，这些点的势能低于周围区域，而这些点并非全局最小势能点。局部最小值可能会误导路径规划，导致路径搜索陷入局部最优而非全局最优。

6.1 局部最小值问题的产生

6.1.1 局部最小值的定义与特征

局部最小值是指在势场函数的某个区域内，存在一个点，在这个点上势场函数的值小于或等于周围所有点的函数值。局部最小值有以下几个特征：

• 局部最小值点周围的势场值要高于该点。
• 通常，势场法在这些点的梯度为零，即力的作用相互抵消。
• 局部最小值点并非总是路径的终点，有时它可能出现在路径中途。

局部最小值问题的产生，会导致路径规划算法无法找到目标位置，或在规划路径中存在无效的循环路径。

6.1.2 局部最小值对路径规划的影响

局部最小值的存在对路径规划的影响是显而易见的：

• 路径可能在局部最小值点停止，无法继续向目标移动。
• 规划出的路径可能不是最短的，或者不是最佳的路径，因为它可能在局部最小值点徘徊。
• 在复杂的环境中，局部最小值可能非常多，这会显著增加路径规划的复杂度。

为了有效地进行路径规划，需要采取措施应对局部最小值问题。

6.2 处理局部最小值的策略

6.2.1 避免局部最小值的算法改进

为了避免局部最小值对路径规划的影响，可以采取以下几种算法改进策略：

• 加入扰动机制 ：在势场函数中引入随机扰动，可以促使路径规划算法跳出局部最小值。
• 梯度修正 ：调整梯度算法，使其在遇到势场值变化缓慢或趋近零时，能够调整搜索方向。
• 势场函数调整 ：通过修改势场函数，比如增加一个吸引目标的势场，确保有指向目标的吸引力。

6.2.2 局部最小值处理的实证研究

在实证研究方面，有许多研究尝试解决势场法中的局部最小值问题，以下是一些有效的方法：

• 动态窗口法 ：通过为机器人在每个时间步设定一个可移动的窗口，动态地调整路径搜索范围和方向。
• 人工势场法与遗传算法结合 ：使用遗传算法优化参数，避免陷入局部最优解。
• 模拟退火法 ：该方法通过模拟物理退火过程，允许在某些情况下接受更差的解，增加跳出局部最小值的可能性。

通过这些策略的实施，可以有效地减少局部最小值对路径规划的影响，提高路径规划的可靠性。

在下一章节中，我们将探讨如何结合全局规划来创建一个更加高级的势场法版本，以此进一步提升路径规划的性能。

本文还有配套的精品资源，点击获取

简介：势场法路径规划是一种模拟物理力场原理，用于为移动机器人或无人车辆在复杂环境中寻找最优路径的技术。本MATLAB程序详细注解了实现过程，包括环境建模、势场构建、力场计算、路径搜索和优化等关键步骤。该程序不仅帮助理解势场法的基本原理和实现细节，还提升了MATLAB编程和数值计算能力，对多个领域具有应用价值。

本文还有配套的精品资源，点击获取