一元三次方程重根判别式_解一元二次方程方法技巧

点击上方蓝字"8020同学社"关注我们哦！

方法一：选择合适的方法解一元二次方程

方法名称	适用范围	说明
直接开平方法	形如x2=p或(mx+n)2=P(p≥0)	方程没有一次项时用直接开平方 法较为简单(最直接的方法)
配方法	适合所有一元二次方程	二次项系数为1，一次项系数为偶数时，用此方法较为简单(最基本的方法)
公式法	适合所有一元二次方程	配方法和公式法中，当各项系数均为整数，且较小时，首选公式法(万能方法)
因式分解法	一边为0，另一边易于分解成两个一次因式的积的形式的一元二次方程	方程没有一次项时用因式分解法较为简单;当方程中含有括号时,不要急于去括号,应观察是否能看作整体,直接因式分解(最简单的方法)

【温馨提示】

在没有规定解法时，解一元二次方程可以按下列次序选择解法：直接开平方法→因式分解法→公式法→配方法. 

Q:

例1用适当的方法解下列方程

(1))3x²-2x-2=0；(2)(x-1)²=3;

(3)2(x-3)=3x(x-3)；(4)x²-2x=4 

A:

解析(1)∵a=3，b=-2，c=-2，

∴b²-4ac=(-2)²-4×3×(-2)=28>0

                                             

(3) 移项得2(x-3) -3x(x-3)=0因式分解得(2-3x)(x-3)=0，

2-3x=0或x-3=0

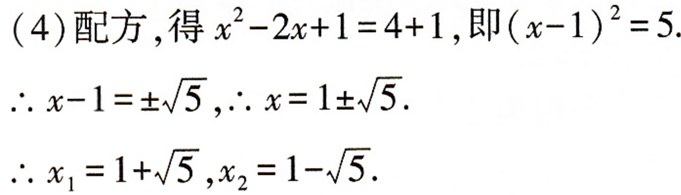
方法二：配方法在二次三项式中的应用方法

在二次三项式中应用配方法与一元二次方程的配方法类似，但也有不同：

(1) 化二次项系数为1.当二次项系数不是1时，可提取次项系数，但不能像解方程那样，除以二次项系数(因为二次三项式配方是恒等变形，而配方法解一元二次方程是同解变形).

(2) 加上一次项系数一半的平方，使其中的三项成为完全平方式，但又要使此二次三项式的值不变，故在加的同时，还要减去一次项系数一半的平方.

(3) 配方后将原二次三项式化为a(x+m)²+n(a≠0)的形式.

Q:

例2阅读材料：把形如ax²+bx+c的二次三项式(或其部分)配成完全平方式的方法叫做配方法配方法是完全平方公式的逆用，即a²±2b+b²=(a±b)².

                                             

的三种不同形式的配方(即“余项”分别是常数项、一次项、二次项——见横线上的部分).

请根据阅读材料解决下列问题：

(1)比照上面的例子，写出x²-4x+2三种不同形式的配方；

(2)将a²+ab+b²配方(至少写出两种形式)；

(3)已知a²+b²+c²-ab-3b-2c+4=0，求a+b+c的值.

A:

(1)x²-4x+2=(x-2)²-2 

                                             

方法三：一元二次方程根的判别式的应用方法

一元二次方程根的判别式的应用主要有以下三种情况：

(1)不解方程，由根的判别式直接判断根的情况；

(2)根据方程根的情况，确定方程中字母系数的取值范围；

(3)应用根的判别式证明方程根的情况(无实根、有两个不相等的实根、有两个相等的实根).

Q:

例3(1)关于x的一元二次方程kx²-3x-1=0有两个不相等的实数根，那么k的取值范围是____.

(2)关于x的方程ax²-2x-1=0有实数根，则a的取值范围是____.

(3)关于x的一元二次方程x²+(2m+1)x+m²-2=0有两个实数根，则m的最小整数解是____.

A:

解(1)∵关于x的一元二次方程kx²-3x-1=0有两个不相等的实数根，

∴k≠0且△=(-3)²-4×k×(-1)>0，                                             

∴△=4+4a≥0，∴a≥-1；

当a=0时，-2x-1=0有实数根，符合题意,

故a的取值范围为a≥-1.

(3) ∵关于x的一元二次方程x²+(2m+1)x+m²-2=0有两个实数根,

△=(2m+1)²-4×1×(m²-2)≥0, 

【温馨提示】

①根据一元二次方程根的情况确定字母参数或取值范围时，不要忽略隐含条件二次项系数不为0，否则这个参数的取值范围会增大，导致解题错误.

②对于形如ax²+bx+c=0的方程有实数根的问题要从a=0和a≠0两个方面去考虑.

方法四：一元二次方程根与系数的关系的应用方法

利用一元二次方程根与系数的关系求关于其根x₁、x₂的代数式的值的关键是把所给的代数式经过恒等变形，化为含x₁+x₂，x₁x₂的形式，然后把x₁+x₂，x₁x₂的值整体代入，即可求出所求代数式的值.

Q:

例4若a，b，是一元二次方程3x²+2x-9=0的两根，则

A:

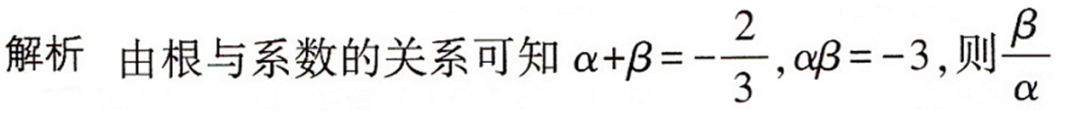
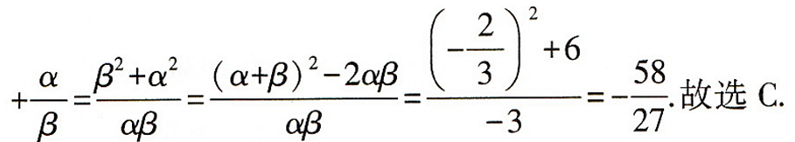
Q:

例5一元二次方程x²-4x+2=0的两根为x₁，x₂，则x₁²-4x₁+2x₁x₂的值为____.

A:

解 ∵一元二次方程x²-4x+2=0的两根为x₁，x₂，

∴x₁-4x₁=-2，x₁x₂=2

x₁²-4x₁+2x₁x₂=-2+2×2=2

答案2