语言已知底和高求三角形面积_三角形中的三角形

最新推荐文章于 2022-04-25 12:35:51 发布

夜雨微亭er

最新推荐文章于 2022-04-25 12:35:51 发布

阅读量690

点赞数

文章标签：语言已知底和高求三角形面积

本文链接：https://blog.csdn.net/weixin_36219894/article/details/112682041

版权

本文探讨了通过三角形的边长比值求解三角形面积的方法，以及如何利用这种方法推导平面几何中的梅涅劳斯定理和塞瓦定理。通过特定的图形构造和比例性质，文章详细展示了内三角形第一公式和第二公式，并指出这些公式在不同特殊情况下的应用，揭示了数学中从特殊到一般的研究方法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

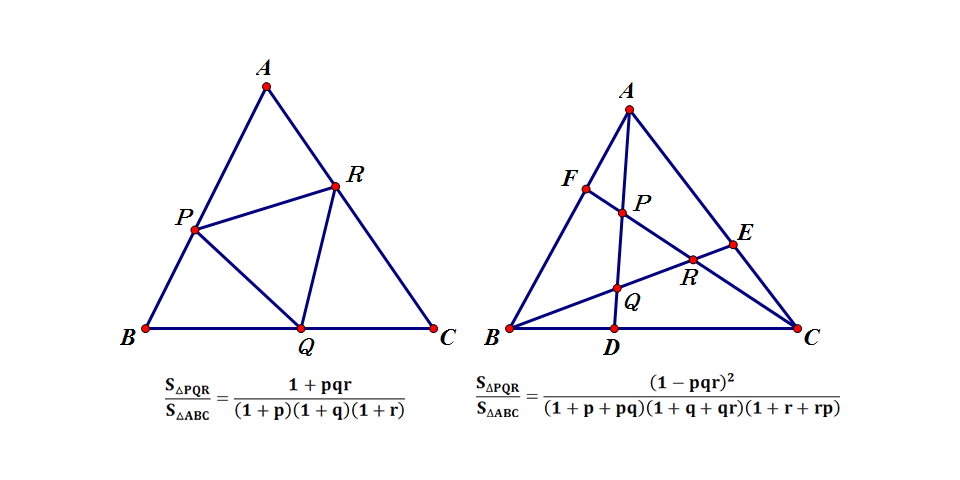
本文将研究两种关于三角形中的平面几何图形，并从中导出三角形面积的关系式，并以此给出平面几何中梅涅劳斯定理与塞瓦定理的一种证明方法。

先来看下面的图形：

内接与

，记

，

的面积为

，

的量表示不变，我们来推导

与

之间的关系。

当我们遇到这样的问题时，由于给出的已知条件是长度的比值，通过这个比值，我们就可以利用比例性质或者是杠杆原理来求出线段的长度，然后在小三角形内使用余弦定理，就可以求出

三边的长度，再利用秦九韶公式，便能够求出

，这种方法虽然可行，但是计算量实在过于庞大，我们应当寻求更为简洁办法。

（注：这里说的杠杆原理是一种利用杠杆平衡的方法来求解几何图形的比例问题，既可以长度，也可以是面积，或者是体积，我们将会在日后的文章单独深入的介绍。）

由于给出的已知条件是长度的比值，那么我们就可以猜想，

与

之间的关系也是一种比值关系，那么我们就可以从面积与面积的比值入手来求解，我们又看到图形中有五个三角形，它们之间存在着有一个共同角度的特点，这让我们想到了公式二，这样面积相比之后，角度可以消除，长度的比值又是已知可求的，于是方法便诞生了。

且看下面的推导：

很明显，

，

之所以选择这两个三角形，一方面是因为关联了已知

，另一方面就是有一个共同的角度A，同时

是联系

的。下面许多的比例式均由此法得到，我们可能会省去中间步骤。

同理：

，

而

，

于是：

。

我们姑且称此式为内三角形第一公式。

可以继续证明，当P、Q、R三点在三边的延长线上时，公式依然成立，只需要将p、q、r冠以正负号，具体符号见下图说明。

首先取定一个方向为正方向，如上图所示，我们以逆时针方向为正方向，即

为正向，那么P在A点B点之间，B点一侧的延长线上p为正，在A点一侧的延长线上为负，BC边上、AC边上同理。

事实上，我们只需要将线段向量化即可，然而有时候，我们只想要带方向的线段长度，而不是向量，我就定义这种带方向的线段长度为线段的数量，用不带箭头的一横表示，例如P在A点一侧的延长线上，

与

就是反向的，那么他们的比值

就是负值，否则就是正值。（注意：向量其实不存在这种除法运算，正确的表达有方向的线段的写法应该是

，这里，我们只是想给出相关的说明。）

特别的，当P、Q、R三点共线时，

的面积就变成了0，同时p、q、r又不可能为-1，所以根据公式，只能是

，即有

，之所以为-1，是因为当P、Q、R三点共线时，一定有一个点在一边的延长线上，如果不计它们的符号，那么则有

，这个结论就是平面几何中的

梅涅劳斯逆定理。如下图所示：

即有：

。

关于梅涅劳斯定理，还有很多其它的证明方法，我们日后将会给出。

如果P、Q、R分别是角平分线与对边的交点，由角平分线定理（见《三角形中的线段》）可知：

，

，代入第一公式，得：

。

如果P、Q、R是三条高线与对边的交点，那么：

，

，代入第一公式，得：

。

我们再来看一看下面的图形：

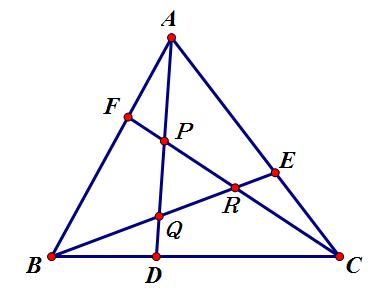
D、E、F分别为BC、CA、AB上的点，AD、BE、CF三条线，两两相交围城了

，我们记

，

，依然探讨

与

之间的关系。

与前面的问题使用同样的思路来推导。

同样的，有：

，

因为：

，

所以：

于是：

在三角形BCE中，以及AD，看成梅涅劳斯定理的利用图形，则有：

，可以得到：

在三角形BCE中，以及AD，看成梅涅劳斯定理的利用图形，则有：

，可以得到：

于是：

同理：

，

所以：

我们姑且称为内三角形第二公式。

当P、Q、R三点重合，即AD、BE、CF三条线段交于一点时，

就变成了0，由上式可得

，这个结论就是平面几何中的

塞瓦定理。如下图所示：

AQ、BR、CP交于一点，即有：

。

关于塞瓦定理，也有许多证明，我们将在日后给出。

总结：本文所讨论的两种几何图形，其特点是由一个三角形三边上的点通过连线所获得的一个新的三角形，这个新三角形在正常情况下处于原三角形的内部，但实际上，边长上的点在其延长线上也是成立的，只是需要引入符号，我们探究了这两个三角形的面积关系，这是两个三角形多种关系中的一种，并以此为基础得出了平面几何中的两个常用的定理，梅涅劳斯定理和塞瓦定理，可以说这是一种间接证明，也可以说是研究面积关系所得到的产物。

启示：从这篇文章里，我们可以受到一些启发，就是如果我们遇到一个问题，比如这里就是证明梅涅劳斯定理，我们其实可以间接研究与其相关问题而得出。也可以说成是当我们想要去探索和研究一个新的东西时，往往会得出意外的惊喜，比如我们本来想要研究两个三角形的面积关系，可没想到却意外地证明了梅涅劳斯定理和塞瓦定理，进而发现，原来它们都是我们研究成果的特例，这种惊喜才是我们真正要从数学那里学习的。