语言已知底和高求三角形面积_小学三角形专项学习——金字塔模型，我是给学奥数用的...

大家好，我是徽乡小居。这里分享一篇关于金字塔模型的专项学习，是专为奥数学生辅导用的。对于一般的学生可以学学其中的知识，看懂即可，可以开拓思维，从而对数学感兴趣。

几何专项：金字塔模型

今天我们将学习相似三角形当中另一个重要模型，金字塔模型。相似三角形具有的一些性质，金字塔模型同样具有。

一、金字塔模型

沙漏模型由一组平行线和一组相交线构成，且相交线的交点在平行线之间。如果交点在两条平行线的同一侧，就会构成一种新的模型，我们形象地称之为金字塔模型。在金字塔模型中也有相应的比例关系。

例1、如图EF与BC平行，AF∶FB＝1∶2。AE＝2，EF＝３，那么CE的长度是多少？AC的长度是多少？BC的长度是多少？

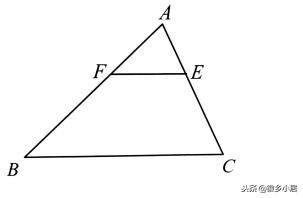
思路分析：由金子塔模型，AE∶EC＝AF∶FB＝１∶２，可求出CE＝２×２＝４，

AC＝２＋４＝６；EF∶BC＝AF∶AB＝１∶(1＋2)＝1∶3，可求出BC＝3×3＝9

练习题

1、如图所示，DE与BC平行，已知AD＝4，BD＝5，DE＝16，则BC的长度是多少？

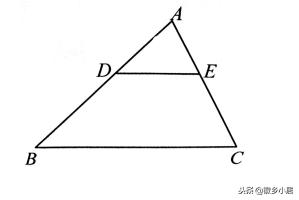
【答案】由金字塔模型，AD：AB=DE：BC=4:9；DE=16,可得出BC=36

例2、如图所示，DE与BC平行，已知AD＝4，BD＝5，△ADE的面积为32则四边形DECB面积是多少？

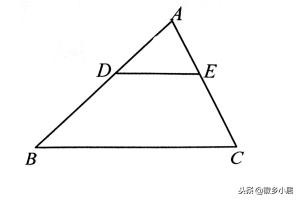
思路分析：由金字塔模型，S_△ADE∶S_△ABC＝AD²∶AB²＝42∶(4＋5)²＝16∶81，可求出S_△ADE＝32÷16×81＝162，所以四边形DEBC的面积是162－32＝130.

练习题

1、如图，直角三角形ABC中，AB＝4，BC＝6。又知BE∶EC＝1∶3，求△CDE的面积。

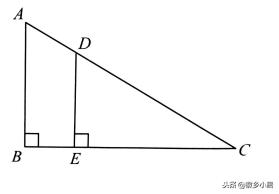
【答案】由金字塔模型知，DE：AB=CE：CB=3:4，则DE=4×3/4=3.又知道CE=6×3/4=4.5，可求出△CDE的面积为3×4.5÷2=6.75。

例3、已知三角形ADE的面积为3平方厘米，D是AB的三等分点(靠近A点)，且DE与BC平行，请求出三角形OBC的面积是多少平方厘米？

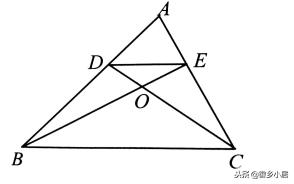
思路分析：图中既有沙漏模型，又有金字塔模型。

由金字塔模型知，AD∶AB＝1∶3，S_△ADE∶S_△ABC＝1∶9，可以求出S_△ABC＝3×9

＝27平方厘米，S_{四边形DECF}＝27－3＝24平方厘米。

由沙漏模型，OD∶OC＝DE∶BC＝AD∶AB＝1∶3，设△ODE的面积为1份，则△ODB的面积为3份，△OEC的面积为3份，△ODB的面积也为3份，△OBC的面积为9份，由此可知△OBC的面积为24÷(1＋3×2＋9)×9＝13.5平方厘米。

练习题

1、如右图所示，三角形ABC中，DE平行BC，DF平行AC，EF平行AB，已知△PQF的面积为54，△ADE的面积为96，那么 三角形ABC的面积是多少？

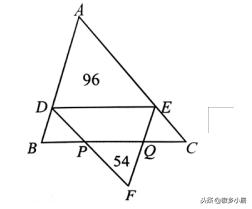
练习题答案

金字塔模型综合练习题

1、如图，三角形ABC的面积是1，D、E、F分别是相应的三等分点，三角形ADO的面积是多少？

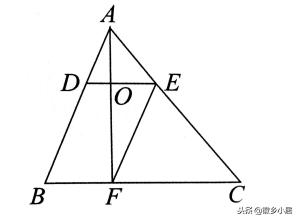
练习题答案，简要过程

2、如图，已知D点是BC的中点，E是AC的中点。三角形ABC由①至⑤这5部分组成，其中①的面积比④多6平方厘米。请问：三角形的面积是多少平方厘米？

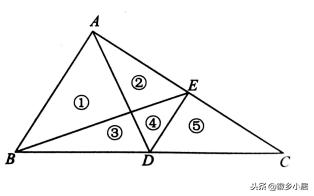
练习题答案，简要过程

3、如图，A、B、C分别是ED、EG、GF的中点，请问：三角形CDO的面积是三角形ABO面积的几倍？

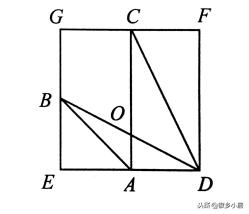
练习题答案，简要过程

4、如图，E、F是正方形ABCD的边AB，BC的中点，如果正方形的面积是１，那么阴影部分的面积是多少？

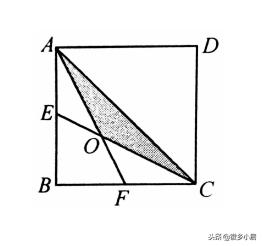
提示：连接OB 答案：1/6

发篇文章挺花时间的，希望对有需要的人带来帮助。欢迎收藏，转发，点赞。更多分享，下期见哦。