和与余数的和同余理解_关于同余问题，比较好理解的一种角度（前篇）

这个方法只能算作“比较好理解”的一种角度，并没有“特别巧妙”，等后面再思考这个问题时，可能会有更简单好懂的理解。

以下内容阅读前要先具备“因数和倍数”一系列知识，包括最大公因数和最小公倍数等等。

这篇来说“同余问题”。

先名词解释，“同余”指的是具有相同余数的数，余数自然和“谁除以谁余几”有关，所以一定是在整数除法中探讨的，自然，同余在整数范围内讨论。

有些小朋友们不想碰“同余问题”的原因，多半是带有“≡”符号的看起来特别不习惯，题目中提到“谁除谁”或者“谁被谁整除”一下子分不清感到乱，又或者是“a和b关于模数c同余”这种看起来得逐字逐词分析的文字有种好烦人的感觉等等。

所以，现在来尝试一下比较好理解的一种方式。

首先说余数。余数的话一定是有除法才有余数，比如8除以3，得到商2余2。要是和“同余”有关，也就是余数得相同，比如15除以13余数也是2，只不过两个被除数8和15没什么联系，两个除数3和13也没什么联系，只是余数相同。换个角度，如果我们规定除数都是3，那么除了8除以3余2之外，20除以3也余2，5除以3也余2，那么把这些除以3都余2的数排列一下：

5，8，11，14，17，20，23，26，29，32，35，38，41，…

别忘了加上2本身，因为2除以3商0余2，所以是：

2，5，8，11，14，17，20，23，26，29，32，35，38，41，…

然后观察。长得跟等差数列似的，每相邻两个数之间都差了3，而3刚好是除数。刚才提到余数和除法有关，那么“除以3”按照基础除法来说，等同于把被除数平均分成3份，如果以上数字都作为被除数，平均分成3份后肯定都要余2，因为2并没有3那么多，所以不够分。挑两个数，一个5，一个14，按照这种方式画个图：

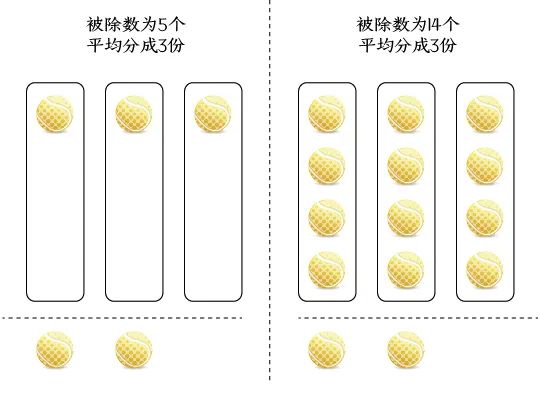
可以