抛物线交点式公式_关于抛物线大题的参考经验（1）：真·经验部分

最新推荐文章于 2021-11-30 18:47:50 发布

行不深

最新推荐文章于 2021-11-30 18:47:50 发布

阅读量3.4k

点赞数

文章标签：抛物线交点式公式

本文链接：https://blog.csdn.net/weixin_36333097/article/details/112351935

版权

本文分享了作者在解决高中数学抛物线大题时的经验，强调设元的重要性，提供了设点不设线的策略，并介绍了过焦点的割线、切线等常见模型及求解技巧。文章还涵盖了三角形面积、最值求解等专题，探讨了消元、均值不等式和求导放缩等方法，适合备考学生参考。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

本文将尝试结合近期数学模拟考试中及各种真题中的解几大题来谈谈本人高中面对抛物线大题时的经验. 由于水平和时间的限制, 本文中一定还有不少的缺点和错误, 恳请各位读者批评指正. 说明：下面的抛物线基本以开口朝右的为例, 当开口朝向不同, 或顶点不同时, 应学会灵活应变.

设元：设点不设线

这在大多数情况下都是很有效的.我高中三年里几乎没有在抛物线大题中将与抛物线相交的直线设为

或

而经常是这样设的——

图1：讲解图(1)

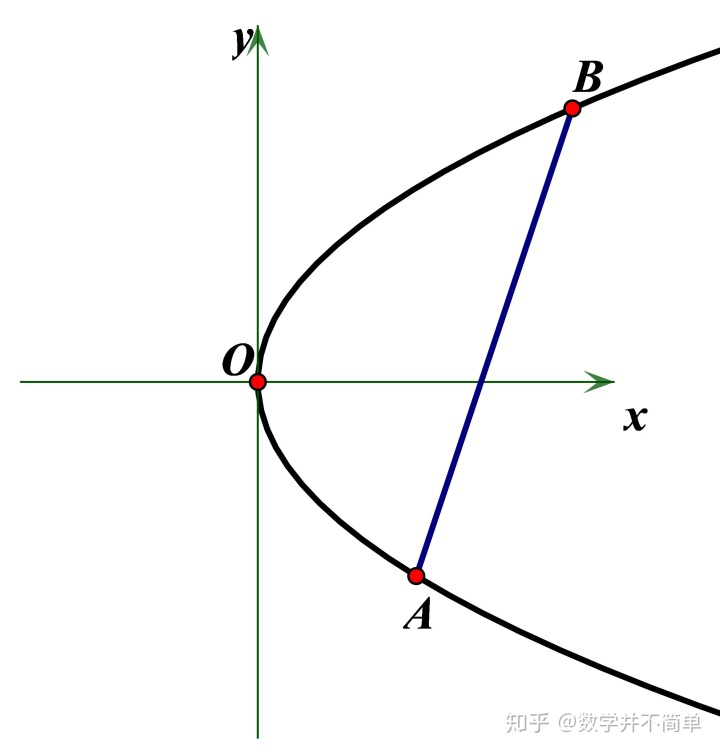
如图1, 图中的抛物线为
设

这样设的好处是, 能非常舒服的表示出三个要素：两个交点, 一条直线. 而如果是设

或

尽管我们可以通过韦达定理得出两个交点坐标的关系, 但每个交点的具体坐标的表达式会很复杂. 当然也有特殊情况, 以后可能会提到.

我们来看下面的例子(第一小问过于平凡, 省略了).

【例1】 (2019/2020宁波期末T21(II)) 已知抛物线
点

在抛物线上, 坐标为

过抛物线的焦点

且不垂直于

轴的直线

交抛物线

于

两点, 动点

满足

的垂心为原点

求证：动点

在定直线

上, 并求

的最小值.

图2：例1

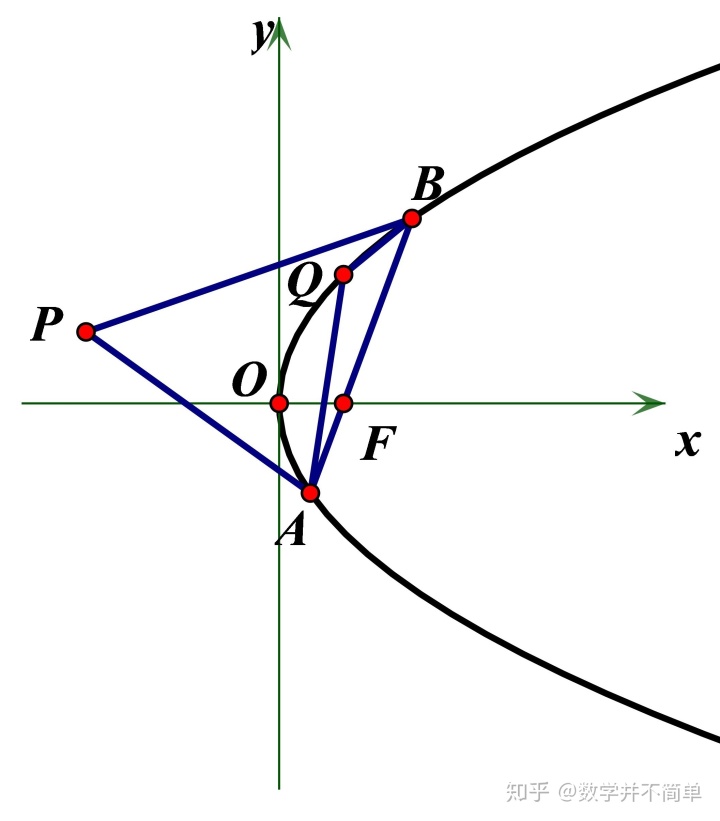
题目中的关键条件是垂心, 正常来讲会转化为三个垂直条件的其中两个, 但无论选哪两个都涉及到

点单个点的性态, 所以设点是个不错的选择.

证明与解 我们设

代入点
有

的垂心为原点

等价于

于是有

故可设出
的方程

由此得出
所以

在定直线

上.

而
点坐标又可以表示为

此时设

则

我们也不难发现, 这里设的

就是

的斜率的倒数, 但如果开始就设

的话我们就没那么容易单独解出

的坐标了. 然后显然可以将面积之比转化为距离之比. 然后就做完了. 具体过程如下.

于是, 我们有

故有

当
时取等. 故最小值为

一些模型

下面会给出一些抛物线大题中的模型, 以及一些相关结论. 值得注意的是, textbf{解答题一般是要求严格写出这些结论的求解过程的. } 将这些结论单列在这里写的主要原因有三: 一是选择题可以省去一些时间; 二是解答题可以用来验证正常求解的正确性; 三是在时间紧张的条件下可以直接写出结论.

我在例题讲解时遇到这些结论时就不多费口舌了.

过焦点的割线

本文中的例1已经出现这样的模型了. 在大题中主要用到的就是下面的结论.

结论1 若图1中抛物线的焦点
在直线

上, 则

(这个结论还是不要直接用了, 毕竟写个直线方程也不是一件难事)

切线

抛物线的切线在大题中是一个非常常见的模型. 如图3, 抛物线方程为

点

的坐标为

点

的坐标为

我们有以下结论.

图3：讲解图(2)

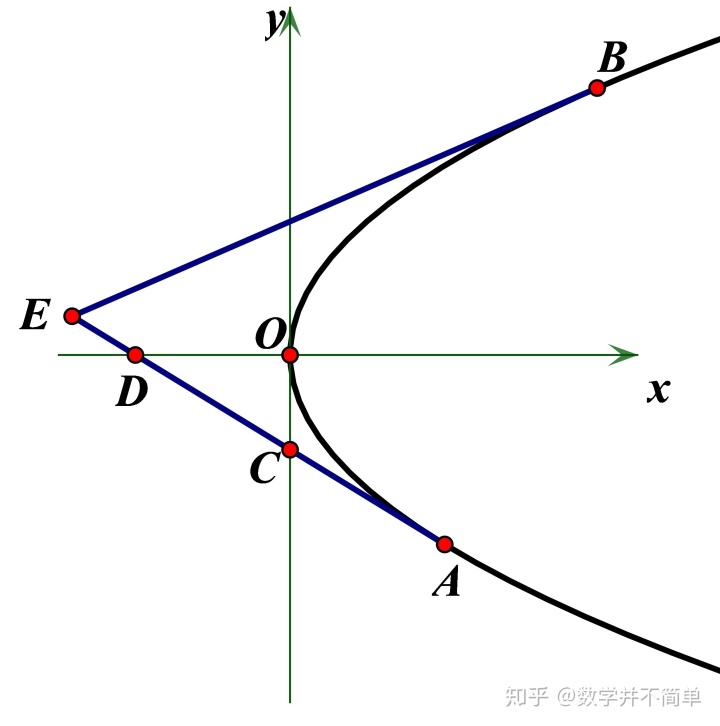
结论2 过
的抛物线的切线方程可表示为

这个结论并不是很好记, 利用下面的结论可以比较容易地表示出切线方程.

结论3 若过
的抛物线的切线与

轴,

轴的交点分别为

则

就是线段

的中点.

由这个结论可以得到

点横坐标为

点横坐标的相反数, 联立

两点快速解出直线方程.

对于两条切线的交点, 我们有这样的结论.

结论4 设过
的抛物线的切线交于点

其坐标为

我们看下面的例子.

【例2】 (2019/2020诸暨期末T21)过抛物线
的焦点

作直线

交抛物线

于

两点, 以

两点为切点作抛物线的切线, 两条切线交于

点.

(I)当直线
平行于

轴时, 求点

的坐标;

(II)当
时, 求直线

的方程.

开口朝向不同于上述结论中的朝向, 要灵活.

解 (I)设点和线为

根据结论4, 点
的坐标为

根据结论1, 知

再根据

平行于

轴, 知

故

做题(II)时要注意去掉上题用到过的条件

(II)我们有

于是有

代入
则

所以
的方程为

或

在题目简洁的条件下求解过程当然最好要写详细. 这里为了说明结论就省略了. 下面同理.

三角形的面积

有一条边平行于坐标轴的三角形的面积一般来说是很好表示的, 下面的结论主要用于处理一般三角形的面积.

结论5 以点
为顶点的三角形的面积可表示为

在没有学过行列式的条件下中式不易看懂, 右式不好记并且比较复杂. 所以我们一般采用后面的结论.

结论6 平面上有点
向量

那么

这个结论一般可以直接用.

上述结论其实在椭圆大题里也有用. 而特别的, 当三个点都在抛物线上时, 我们有更具体的结论.

结论7 以抛物线
上点

为顶点的三角形的面积可表示为

我们看下面的例子.

【例3】 (2019/2020湖州期末T21)已知点
是抛物线

的焦点, 直线

与抛物线

相切于点

连结

交抛物线于另一点

过点

作

的垂线交抛物线

于另一点

(I)若
求直线

的方程;

(II)求三角形
面积

的最小值.

图4：例3

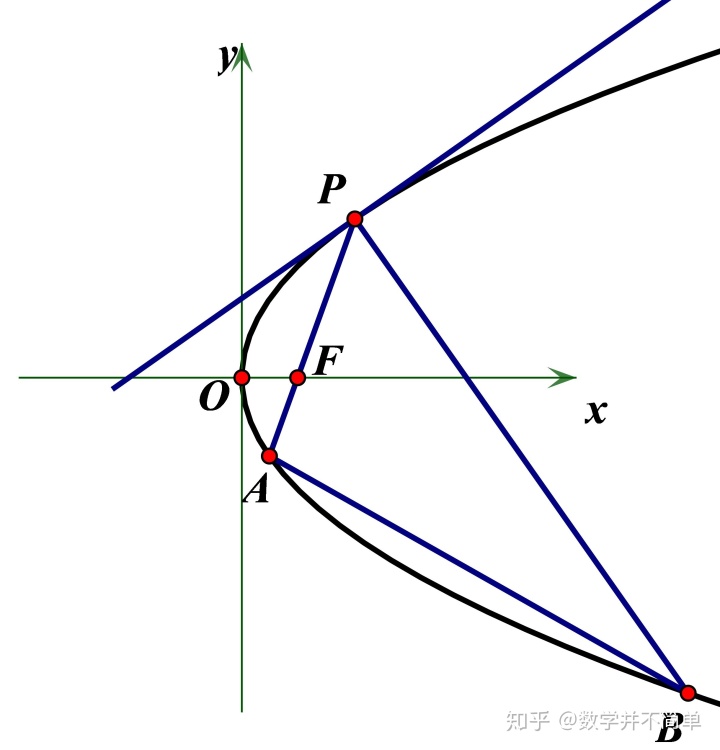
比较简单, 可以一步到位.

解 (I)设点为
由

知

故根据结论2,
可化简为

(II)本题去掉
的条件. 根据结论1知

根据结论2,

又知

由两直线垂直知

因此我们有
于是根据结论7, 三角形面积可表示为

当
即

时取等. 故三角形面积的最小值为

做题技术

高考抛物线大题大部分都是求最值, 其他还有一部分是证明、求取值范围、求值等. 所以下面的技术主要是针对如何求取最值. 对于其他的题目方法其实是类似的.

消元

求最值需要不等式放缩, 但放缩的前提是有一个便于放缩的式子, 而一般来说, 我们会希望这个式子是单变元的. 但我们设的元很可能不止一个, 因此我们需要通过消元将需要求的东西消成只含单变元的式子.

而我们消元一般有这样两种方法——

一、将其他未定元表示成其中一个未定元的形式.

例3就是一个好例子, 题中我们设出了

三个未定元, 根据提给信息得出了两个分别为

和

之间的关系式, 所以我们很自然的用

来表示

然后表示出三角形的面积, 结果也是非常理想. 这就是第一种方法. 值得注意的是, 在这个例子中, 用

表示

的结果也是很理想, 但如果要尝试用

表示

就会使问题变得繁琐, 因为用

表示出的

含根号, 表达式非常复杂, 相应

也会很复杂. 因此, 采取第一种方法进行消元时, 我们要选择一个合适的未定元, 并将其他的元表示成含该元的表达式.

二、将其他未定元表示成一个新的未定元的形式.

例1就是一个非常简单的例子, 题中我们设出了

两个未定元, 而待放缩的式子中都是

的形式, 于是我们会想到用

代替

和第一种方法类似, 我们要找一个合适的新变元. 使得待放缩式为只含单变元的简单式.

下面是一些关于放缩的技术.

运用均值不等式放缩

均值不等式在解几大题里一般是指算整数术平均值大于几何平均值, 即若

且

则

例1与例3都是简单的例子, 它们都是用到了二元均值不等式的化简形式:

其他还有别的例子, 下一部分会给出.

求导放缩

求导放缩就是把已知式或其中的一部分当作函数, 利用求导来探索所求式值关于未定元的单调性, 从而得出最值的方法. 说起来很容易, 我们来看下面的例子.

【例4】 (2019/2020台州期末T21)如图5, 过点
作直线

交抛物线

于

两点(点

在

之间), 设点

的纵坐标分别为

过点

作

轴的垂线交直线

于点

(I)求证：

(II)求
的面积

的最大值.

图5：例4

问题开始的部分非常简单, 我们可以一步到位.

证明与解 (I)根据已知条件
则

由于

在直线

上, 所以

证毕！

(II)
又

所以

所以

代入(I)中得到的
知

于是我们来到了求最值环节, 首先我们不难发现, 我们要限定

的范围, 否则当其绝对值趋于无穷大时, 面积也会趋于无穷大. 这里限制就需要用到还没有使用的条件“点

在

之间”.

因为点
在

之间, 所以

故

即

所以

为求最值, 我们将待放缩式求导, 并寻找极值点.

设
则

当

时,

故

在

上单调递增, 同理可知

在

上单调递减. 故

在

上的最大值为

区间内去掉

后最值不变, 故三角形面积的最大值为

值得一提的是, 本题我们也可以采用均值不等式进行处理.

因为
所以

当
即

时取等. 故三角形面积的最大值为

面对分式的放缩

这里的分式主要指分子和分母都是多项式的式子. 对于这种式子求最值方式作分类讨论没有什么意义, 我们来看一个非常经典(?)的例子.(这里第一小问过于基础, 此处从略)

【例5】 (2019浙江卷T21(II))如图6, 已知抛物线
过抛物线的焦点

的直线交抛物线于

两点, 点

在抛物线上, 使得

的重心

在

轴上, 直线

交

轴于点

且

在点

的右侧. 记

的面积分别为

求

的最小值及此时点

的坐标.

图6：例5

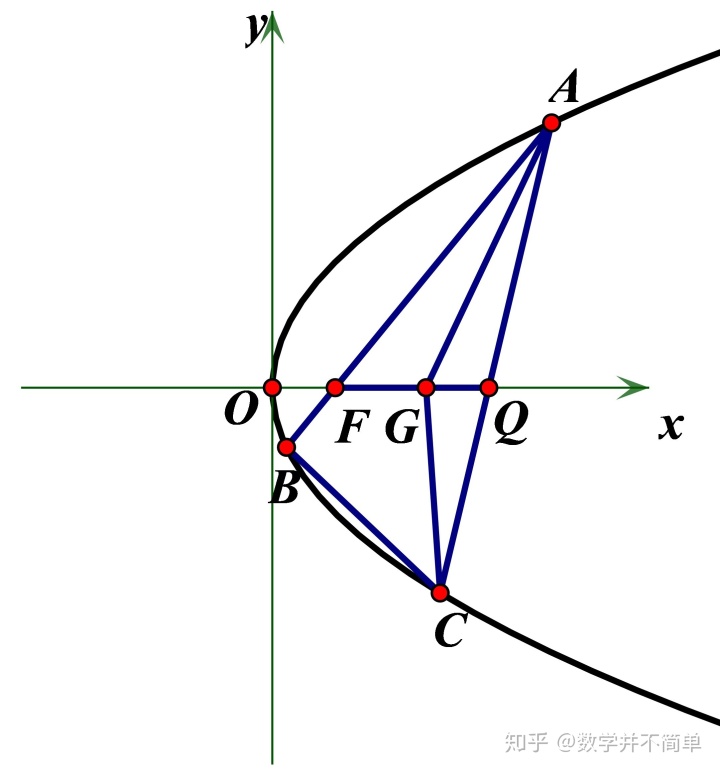
作为一道纯种浙江高考题, 这道题很复杂, 我们一步一步来. 首先是设元, 并列出不同元之间的关系.

解设
则

所以

点

为

的重心, 所以

由于

在

轴上, 所以

根据结论1,

又由于

在

右侧, 故

其后我们进行消元, 依赖关系式

和

注意到

可以互相简单地表示, 且

就是

的相反数, 所以将

或

作为单变元都是合理的选择. 我们这里把

作为单变元.

根据关系式, 我们有

于是

于是

所以
所以

于是面积比可以表示为

其实这道题在列出表达式过程中还有一个关键的因式分解步骤, 即分子分母同时提出和约去

这个想法很自然, 就不做深入探讨了.

于是我们将要求的面积比写成了只含单变元

的分式, 进入了放缩阶段. 首先我们注意到每一个

都是以

的形式在待放缩式中出现的, 所以自然想到换元代替

设
则

于是我们得到了一个分子分母均为二次多项式的分式, 这种式子我们并不是很容易处理., 所以我们不难想到对分子分母进行降次, 而降次方法类似于我们小学学习过的假分数化为带分数, 即将原式改写成一个数加上一个分子降次分母不变的分式, 像下面这样.

显然边上的

对放缩不会有什么影响, 所以我们只要考虑对边上的分式进行放缩, 其中分式的分子为一次多项式, 分母为二次多项式. 做到这一步对

进行求导也可以解决问题, 但我们这里给出一种更直接的方法. 我们由浅入深地看这几个关于正数

的分式:(1)

(2)

(3)

(4)

其中(1)就是我们很熟悉的对勾函数, 我们可以不加证明地给出下列结论.

结论8 对于对勾函数

(I)当
时, 函数在区间

上单调递增, 在区间

上单调递减. 特别地,

在

上的值域均为

在

上有最小值点

对应最小值为

在

上的值域均为

在

上有最大值点

对应最小值为

(II)当
时,函数在区间

上均单调递增, 在两个区间内的值域均为