双曲线和直线联立公式_【巧课易分享】高中数学：直线与抛物线的位置关系

巧课易教育

【基础回顾】 一、课本基础提炼 1．研究直线与抛物线的位置关系,一般是联立两曲线方程,但涉及抛物线的弦长、中点、距离等问题时,要注意“设而不求”、“整体代入”、“点差法”以及定义的灵活应用． 2．有关直线与抛物线的弦长问题,要注意直线是否过抛物线的焦点,若过抛物线的焦点,可直接使用公式|AB|＝x₁＋x₂＋p,若不过焦点,则必须用一般弦长公式 二、二级结论必备 过抛物线焦点的动直线与抛物线交于点A,B,则该抛物线在点A,B处的两切线的交点轨迹是抛物线的准线. 【技能方法】 1.直线与抛物线相交时的弦长问题 若直线过抛物线焦点,则求直线被抛物线截得的弦长|AB|,常用|AB|＝x₁＋x₂＋p；若直线不过抛物线焦点,则求直线被抛物线截得的弦长|AB|,常用,对于此类问题,应熟练地利用韦达定理设而不求计算弦长,另外注意与面积有关的问题,常用到弦长公式. 

例1．已知抛物线C：y²＝2px(p＞0)的焦点为F,若过点F且斜率为1的直线与抛物线相交于M,N两点,且|MN|＝8. (1)求抛物线C的方程； (2)设直线l为抛物线C的切线,且l∥MN,P为l上一点,求的最小值． 【解析】 (1)由题可知F, 则该直线方程为 代入y²＝2px(p＞0),得 设M(x₁,y₁),N(x₂,y₂), 则有x₁＋x₂＝3p. ∵|MN|＝8, ∴x₁＋x₂＋p＝8,即3p＋p＝8,解得p＝2, ∴抛物线的方程为y²＝4x. (2)设直线l的方程为y＝x＋b,代入y²＝4x,得x²＋(2b－4)x＋b²＝0. ∵l为抛物线C的切线,∴Δ＝0,解得b＝1. ∴l的方程为y＝x＋1. 设P(m,m＋1),则＝(x₁－m,y₁－(m＋1)),＝(x₂－m,y₂－(m＋1)), ∴＝(x₁－m)(x₂－m)＋[y₁－(m＋1)][y₂－(m＋1)] ＝x₁x₂－m(x₁＋x₂)＋m₂＋y₁y₂－(m＋1)(y₁＋y₂)＋(m＋1)². 由(1)可知：x₁＋x₂＝6,x₁x₂＝1, ∴(y₁y₂)²＝16x1x2＝16,y₁y₂＝－4.  , ＝1－6m＋m²－4－4(m＋1)＋(m＋1)² ＝2(m²－4m－3)＝2[(m－2)²－7]≥－14, 当且仅当m＝2,即点P的坐标为(2,3)时,的最小值为－14. 例２.抛物线y²=4x的顶点为O,点A的坐标为(5,0),倾斜角为的直线l与线段OA相交(不经过点O或点A)且交抛物线于M、N两点,求△AMN面积最大时直线l的方程,并求△AMN的最大面积. 【解析】由题意,可设l的方程为y=x+m,－5＜m＜0. 由方程组,消去y,得x²+(2m－4)x+m²=0 ,① ∵直线l与抛物线有两个不同交点M、N, ∴方程①的判别式Δ=(2m－4)²－4m²=16(1－m)＞0, 解得m＜1,又－5＜m＜0,∴m的范围为(－5,0) 设M(x₁,y₁),N(x₂,y₂)则x₁+x₂=4－2m,x₁•x₂=m²,  点A到直线l的距离为 ,从而=4(1－m)(5+m)²  ,当且仅当2－2m=5+m,即m=－1时取等号. 故直线l的方程为y=x－1,△AMN的最大面积为 ２．抛物线的中点弦问题. 解圆锥曲线的中点弦问题的一般方法是：联立直线和圆锥曲线的方程,借助于一元二次方程的根的判别式、根与系数的关系、中点坐标公式及参数法求解.若设直线与圆锥曲线的交点(弦的端点)坐标为A(x₁,y₁)、B(x₂,y₂),将这两点代入圆锥曲线的方程并对所得两式作差,得到一个与弦AB的中点和斜率有关的式子,可以大大减少运算量.我们称这种代点作差的方法为“点差法”. 例３．已知抛物线y²=4x的一条弦的斜率为3,它与直线交点恰为这条弦的中点M,则点M的坐标为_______． 【解析】 设弦端点P(x₁,y₁)、Q(x₂,y₂),弦PQ的中点M(x₀,y₀),则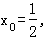x₁+x₂=2x₀=1,y₁+y₂=2y₀, 又 两式相减得(y₁+y₂)(y₁-y₂)=4(x₁-x₂) 即2y₀(y₁-y₂)=4(x₁-x₂),  ∴点M的坐标为 3.抛物线的切线问题 由于抛物线x²=2py(p≠0),可转化为函数,因此我们可以借助导数的几何意义来研究抛物线的切线. 例4. 已知抛物线x²＝2y,过抛物线的焦点F的直线l交抛物线于P,Q两点,过P,Q分别作抛物线的切线,两切线交于点A,则点A的纵坐标为________． 【解析】 由x²＝2y,得,∴y′＝x.设P(x₁,y₁),Q(x₂,y₂),∴抛物线在P,Q两点处的切线的斜率分别为x₁,x₂,∴过点P的抛物线的切线方程为y－y₁＝x₁(x－x₁),又∴切线方程为,同理可得过点Q的切线方程为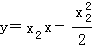,两切线方程联立解得 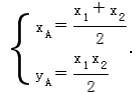又抛物线焦点F的坐标为,易知直线l的斜率存在,可设直线l的方程为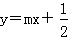,由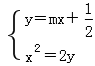,得x²－2mx－1＝0,所以x₁x₂＝－1,所以 ４．面积问题 求三角形或四边形的面积最值是高考中的常见问题,解决这类问题的基本方法是把面积表示为某一变量的函数,再转化为函数求最值,或利用基本不等式求最值. 例５．已知F为抛物线y2＝x的焦点,点A,B在该抛物线上且位于x轴的两侧,OA→•OB→＝2(其中O为坐标原点),则△ABO与△AFO面积之和的最小值是(　　) A．2

B．3 

 【解析】 设直线AB的方程为x＝ny＋m(如图), A(x₁,y₁),B(x₂,y₂), ∴x₁x₂＋y₁y₂＝2.  ∴y₁y₂＝－2. 联立得y²－ny－m＝0, ∴y₁y₂＝－m＝－2, ∴m＝2,即点M(2,0)． 又S_△ABO＝S_△AMO＋S_△BMO     当且仅当时,等号成立． 例６．已知抛物线y²=2px(p＞0),过动点M(a,0)且斜率为1的直线l与该抛物线交于不同的两点A、B,且|AB|≤2p. (1)求a的取值范围. (2)若线段AB的垂直平分线交x轴于点N,求△NAB面积的最大值.【解析】 (1)设直线l的方程为：y=x－a,代入抛物线方程得(x－a)²=2px,即x²－2(a+p)x+a²=0 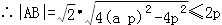.∴4ap+2p²≤p²,即4ap≤－p² 又∵p＞0, (2)设A(x₁,y₁)、B(x₂,y₂),AB的中点 C(x,y), 由(1)知,y₁=x₁－a,y₂=x₂－a,x₁+x₂=2a+2p, 则有 ∴线段AB的垂直平分线的方程为y－p=－(x－a－p),从而N点坐标为(a+2p,0) 点N到AB的距离为 从而 当a有最大值时,S有最大值为 ５.对称问题 根据圆锥曲线上存在不同两点关于某直线对称求参数范围，是一类典型问题，解决此类对称问题,要抓住三点： (1)中点在对称轴上； (2)两个对称点的连线与对称轴垂直； (3)两点连线与曲线有两个交点,故Δ＞0.一般通过“设而不求”、“点差法”得到对称点连线的方程,再与曲线方程联立,由判别式不等式求出参数范围. 例7.已知抛物线y＝ax²－1(a≠0)上总有关于直线x＋y＝0对称的相异两点,求a的取值范围. 解： 设A(x₁,y₁)和B(x₂,y₂)为抛物线y＝ax²－1上的关于直线x＋y＝0对称的两相异点,则 两式相减,得y₁－y₂＝a(x₁－x₂)(x₁＋x₂). 再由x₁≠x₂,得 设线段AB的中点为M(x₀,y₀),则 由M点在直线x＋y＝0上,得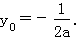 ∴直线AB的方程为 联立直线AB与抛物线的方程并消去y,得 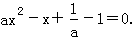 依题意,上面的方程有两个相异实根,  ∴a的取值范围是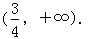 【基础达标】 1.(2014•潍坊模拟)过抛物线y²＝4x的焦点且斜率为的直线l与抛物线y²＝4x交于A,B两点,则|AB|的值为(　　) 

 【答案】A 【解析】 设A(x₁,y₁),B(x₂,y₂),抛物线的焦点为(1,0),则直线l的方程为,代入抛物线方程得3x²－10x＋3＝0. 根据抛物线的定义,可知|AB|＝x₁＋1＋x₂＋1＝ ２．已知直线y=k(x+2)(k＞0)与抛物线C:y²=8x相交A、B两点,F为C的焦点.若|FA|=2|FB|,则k=(　　) 　　

 　　　

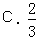
 【答案】Ｄ 【解析】 由直线方程知直线过定点即抛物线焦点(2,0),由|FA|=2|FB|知x_A+2=2(x_B+2) 联立方程用根与系数关系可求 ３．抛物线y=ax²与直线y=kx+b(k≠0)交于A、B两点,且此两点的横坐标分别为x₁,x₂,直线与x轴交点的横坐标是x₃,则恒有(　　) A.x₃=x₁+x₂ B.x₁x₂=x₁x₃+x₂x₃ C.x₁+x₂+x₃=0 D.x₁x₂+x₂x₃+x₃x₁=0 【答案】B 【解析】 解方程组,得ax²－kx－b=0,可知,代入验证即可. ４已知抛物线C的顶点坐标为原点,焦点在x轴上,直线y=x与抛物线C交于A,B两点,若P(2,2)为AB的中点,则抛物线C的方程为_______． 【答案】 y²=4x 【解析】 设抛物线为y²＝kx,与y＝x联立方程组,消去y, 得：x²－kx＝0, x₁+x₂＝k＝2×2,故y²=4x. 【能力提升】 1.设抛物线x²＝12y的焦点为F,经过点P(2,1)的直线l与抛物线相交于A,B两点,若点P恰为AB的中点,则|AF|＋|BF|＝(　　) A.12　　　

B.10 C.6　　　 

D.8 【答案】D 【解析】 设点A(x₁,y₁),B(x₂,y₂),则有y₁＋y₂＝2×1＝2,|AF|＋|BF|＝(y₁＋3)＋(y₂＋3)＝(y₁＋y₂)＋6＝8.故选D. 2.已知双曲线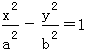(a＞0,b＞0)的两条渐近线与抛物线y²＝2px(p＞0)的准线分别交于A,B两点,O为坐标原点.若双曲线的离心率为2,△AOB的面积为3,则p＝(　　) A.1　　

 C.2　　

D.3 【答案】C 【解析】 由双曲线的离心率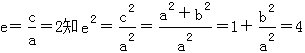.∴双曲线的渐近线方程为.由题意可设得p＝2或－2(舍去).故选C. 3.直线y＝x－3与抛物线y²＝4x交于A,B两点,过A,B两点向抛物线的准线作垂线,垂足分别为P,Q,则梯形APQB的面积为(　　) A．48　　

B．56 C．64　

D．72 【答案】A 【解析】 由题不妨设A在第一象限,联立y＝x－3和y²＝4x可得A(9,6),B(1,－2),而准线方程是x＝－1,所以|AP|＝10,|QB|＝2,|PQ|＝8, 故S_梯形APQB＝(|AP|＋|QB|)•|PQ|＝48. 4.过点(2,4)作直线与抛物线y²＝8x有且只有一个公共点,则这样的直线有条_______． 【答案】 2【解析】 注意到点(2,4)是抛物线上的点,用数形结合知满足题意的直线有两条,其一是过该点的切线；其二是过该点且与对称轴平行的直线.故填2.5.设F为抛物线C：y²＝4x的焦点,过点P(－1,0)的直线l交抛物线C于A,B两点,点Q为线段AB的中点.若FQ＝2,则直线l的斜率等于_______． 【答案】±1 【解析】 设A(x₁,y₁),B(x₂,y₂),直线l的方程为y＝k(x＋1),联立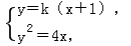得k²x²＋(2k²－4)x＋k²＝0,x₁＋x₂y₁＋y₂＝k(x₁＋x₂)＋2k＝,设Q(x₀,y₀),则,又F(1,0),,解得k＝±1 【终极突破】 1.(2015福建文19)已知点F为抛物线E：y²=2px(p＞0)的焦点,点A(2,m)在抛物线E上,且|AF|=3． (1)求抛物线E的方程； (2)已知点G(-1,0) ,延长AF交抛物线E于点B, 求证：以点F为圆心且与直线GA相切的圆,必与直GB相切． 【答案】 (1)y²=4x； (2)见解析 【解析】 (1)由抛物线的定义得．因为|AF|=3,即,解得p=2, 所以抛物线E的方程为y²=4x． (2)解法一：因为点A(2,m),在抛物线E：y²=4x上, 所以,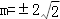由抛物线的对称性,不妨设 由,F(1,0)可得直线AF的方程为 ,得2x²-5x+2=0. 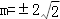解得x=2或,从而 又G(-1,0),所以 所以k_GA+K_GB=0,从而∠AGF=∠BGF,这表明点F到直线GA,GB的距离相等, 故以F为圆心且与直线GA相切的圆必与直线GB相切． 解法二：设以点F为圆心且与直线GA相切的圆的半径为r． 因为点A(2,m)在抛物线E：y²=4x上, 所以,由抛物线的对称性,不妨设 由,F(1,0)可得直线AF的方程为 ,得2x²-5x+2=0. 解得x=2或,从而 又G(-1,0),故直线GA的方程为 从而 又直线GB的方程为 所以点F到直线GB的距离 这表明以点F为圆心且与直线GA相切的圆必与直线GB相切． 2.设不同的两点A(x₁,y₁),B(x₂,y₂)在抛物线y＝2x²上,l是AB的垂直平分线. (1)当且仅当x₁＋x₂取何值时,直线l经过抛物线的焦点F？证明你的结论； (2)当直线l的斜率为2时,求l在y轴上的截距的取值范围. 【答案】 (1) x₁＋x₂＝0 ； (2)  【解析】 (1)F∈l⇔|FA|＝|FB|⇔A,B两点到抛物线的准线的距离相等,∵抛物线的准线是x轴的平行线,y₁≥0,y₂≥0,依题意y₁,y₂不同时为0,∴上述条件等价于 ∵x1≠x2,∴上述条件等价于x₁＋x₂＝0,即当且仅当x₁＋x₂＝0时,l经过抛物线的焦点F. 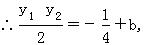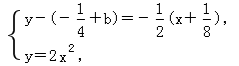(2)设l在y轴上的截距为b,依题意得l的方程为  由y＝2x²,得 过A,B的直线方程为∵直线AB与抛物线有两个不同交点,∴联立得32x²＋8x＋5－16b＝0,Δ＝－9＋32b＞0,.因此直线l在y轴上截距的取值范围是 3.如图,已知直线l与抛物线x²＝4y相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为(2,0)． (1)若动点M满足,求点M的轨迹C； (2)若过点B的直线l′(斜率不等于零)与(1)中的轨迹C交于不同的两点E,F(E在B,F之间),试求△OBE与△OBF面积之比的取值范围． 【答案】 (1) 以原点为中心,焦点在x轴上,长轴长为,短轴长为2的椭圆； (2)  【解析】 (1)由x²＝4y,得  ∴直线l的斜率为y′|_x＝2＝1, 故直线l的方程为y＝x－1, ∴点A坐标为(1,0)． 设M(x,y),则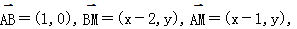 由得整理得 ∴动点M的轨迹C为以原点为中心,焦点在x轴上,长轴长为,短轴长为2的椭圆． (2)由题意知直线l′的斜率存在且不为零, 设l′的方程为y＝k(x－2)(k≠0),① 将①代入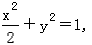 整理,得(2k²＋1)x²－8k²•x＋(8k²－2)＝0, 由Δ＞0得 设E(x₁,y₁),F(x₂,y₂),    由此可得,且0＜λ＜1. 由②知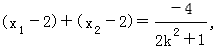 (x₁－2)•(x₂－2)＝x₁x₂－2(x₁＋x₂)＋4       又∵0＜λ＜1, ∴△OBE与△OBF面积之比的取值范围是