ANNOY索引算法

Annoy向量检索算法

官方包：https://github.com/spotify/annoy
(gensim自带AnnoyIndexer)
https://medium.com/@kevin_yang/

python 接口

pip install --user annoy

AnnoyIndex(f, metric) #返回一个只读索引，存储f维向量. Metric可以是 "angular", "euclidean", "manhattan", "hamming", or "dot".
a.add_item(i, v) # 添加item i (非负整数) 和对应的向量. 会给分配max(i)+1的空间
a.build(n_trees, n_jobs=-1) #生成一个由n_trees组成的森林。更多的树会有更高的精确度.生成之后，不能再添加别的item. n_jobs代表生成森林时的线程个数. n_jobs=-1代表使用所有的CPU核.
a.save(fn, prefault=False) #保存索引
a.load(fn, prefault=False) #加载索引文件。将会把所有数据加载到内存中 (using mmap with MAP_POPULATE). Default is False.
a.unload() #unloads.
a.get_nns_by_item(i, n, search_k=-1, include_distances=False) #returns the n closest items. During the query it will inspect up to search_k nodes which defaults to n_trees * n if not provided. search_k代表时间和准确率和速度的折中. include_distances为True将会返回两个item和distance
a.get_nns_by_vector(v, n, search_k=-1, include_distances=False) #same but query by vector v.
a.get_item_vector(i) #返回第i item的vector
a.get_distance(i, j) #返回i和j的距离. NOTE: this used to return the squared distance, but has been changed as of Aug 2016.
a.get_n_items() #返回索引的数据的个数
a.get_n_trees() #返回索引的树的个数
a.on_disk_build(fn) #prepares annoy to build the index in the specified file instead of RAM (execute before adding items, no need to save after build)
a.set_seed(seed) #will initialize the random number generator with the given seed. Only used for building up the tree, i. e. only necessary to pass this before adding the items. Will have no effect after calling a.build(n_trees) or a.load(fn).

注意：
没有对值执行边界检查，因此要小心。
使用归一化向量的欧几里德距离作为其角度距离，对于两个向量u，v等于sqrt（2（1-cos（u，v）））

n_tree在构建期间提供，并影响构建时间和索引大小。值越大，结果越准确，但索引越大。
search_k是在运行时提供的，会影响搜索性能。值越大，结果越准确，但返回时间越长。
如果未提供search_k，它将默认为n*n_tree，其中n是近似最近邻的数目。
否则，search_k和n_tree基本上是独立的，即如果search_k保持不变，n_tree的值不会影响搜索时间，反之亦然。
基本上，考虑到您可以负担的内存量，建议将n_tree设置得尽可能大，并且考虑到查询的时间限制，建议将search_k设置得尽可能大。

示例：

def __init__(self):
	self.index = AnnoyIndex(self.dim, 'angular')   # Length of item vector that will be indexed
	for i in range(len(self.vectors)):
	    self.index.add_item(i, self.vectors[i])
	    
	self.index.build(5) # 5 trees
	self.index.save(annoy_path)
	self.index.load(annoy_path) # super fast, will just mmap the file


def search(self, input_v):
      input_shape = input_v.shape
      candidates = []
      for i in range(input_shape[0]):
          input_i = np.array(input_v[i,:]).reshape(-1,1)
          candi_ids_i = self.index.get_nns_by_vector(input_i, self.top_k, search_k=-1, include_distances=False)

          candi_i = []
          ids = set()
          for i in range(self.top_k):
              id_i = self.id_lists[candi_ids_i[i]]
              if candi_ids_i[i] in ids:
                  continue
              vector_i = np.array(self.index.get_item_vector(candi_ids_i[i])).reshape(-1,1)
              dis_i = cos_sim(input_i, vector_i)
              candi_i.append((id_i, dis_i[0]))
              ids.add(id_i)
          candidates.append(candi_i)
      return candidates

C++接口

#include “annoylib.h”.

参考

https://blog.csdn.net/lsp1991/article/details/78127754
https://blog.csdn.net/lsp1991/article/details/78127754

算法目标

annoy 算法的目标是建立一个数据结构能够在较短的时间内找到任何查询点的最近点，在精度允许的条件下通过牺牲准确率来换取比暴力搜索要快的多的搜索速度。

算法流程

1: 建立索引

Annoy的目标是建立一个数据结构，使得查询一个点的最近邻点的时间复杂度是次线性。
Annoy 通过建立一个二叉树来使得每个点查找时间复杂度是O(log n)。

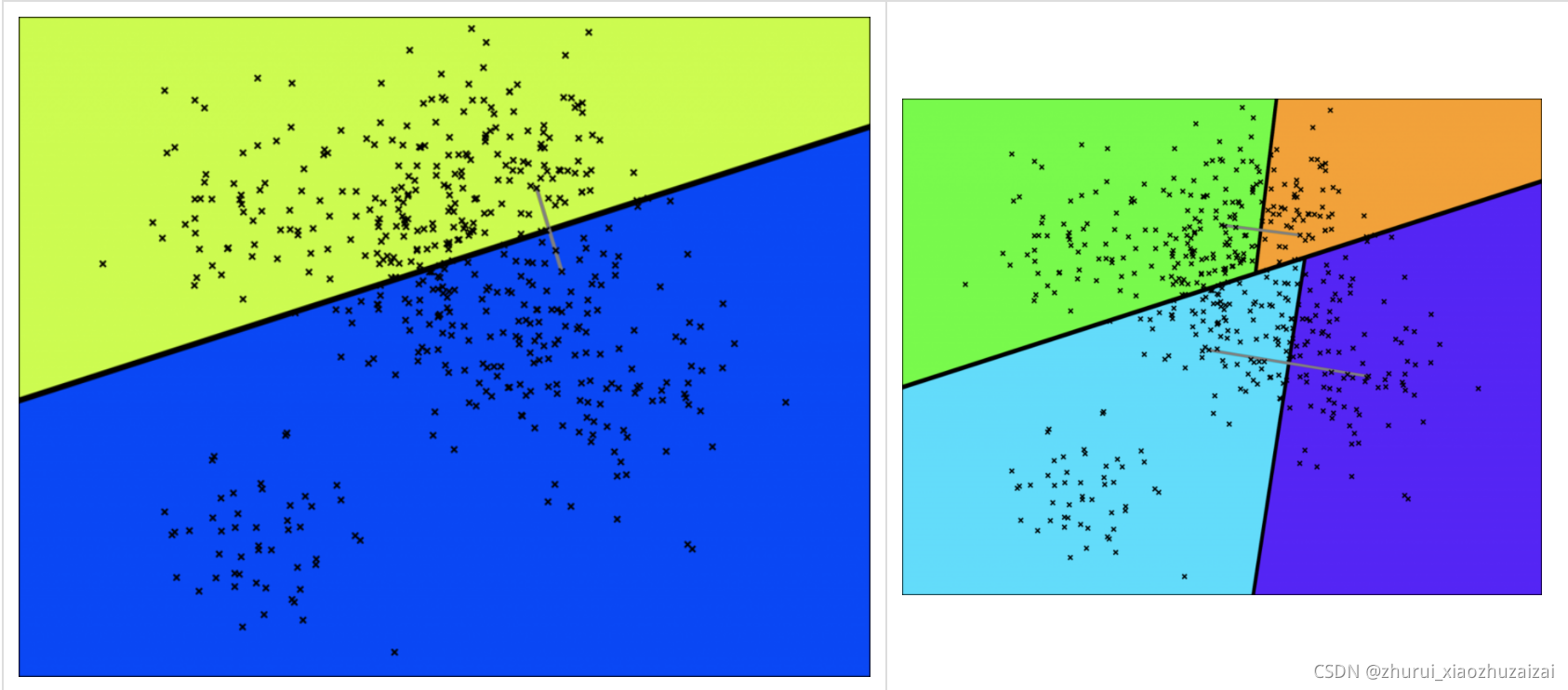
看下面这个图，随机选择两个点，以这两个节点为初始中心节点，执行聚类数为2的kmeans过程，最终产生收敛后两个聚类中心点。这两个聚类中心点之间连一条线段（灰色短线），建立一条垂直于这条灰线，并且通过灰线中心点的线（黑色粗线）。这条黑色粗线把数据空间分成两部分。在多维空间的话，这条黑色粗线可以看成等距垂直超平面。

接下里在超平面分割后的字空间内按照同样的方法继续确定超平面分割字空间，通过这样的方法我们可以将子空间的从属关系用二叉树来表示：

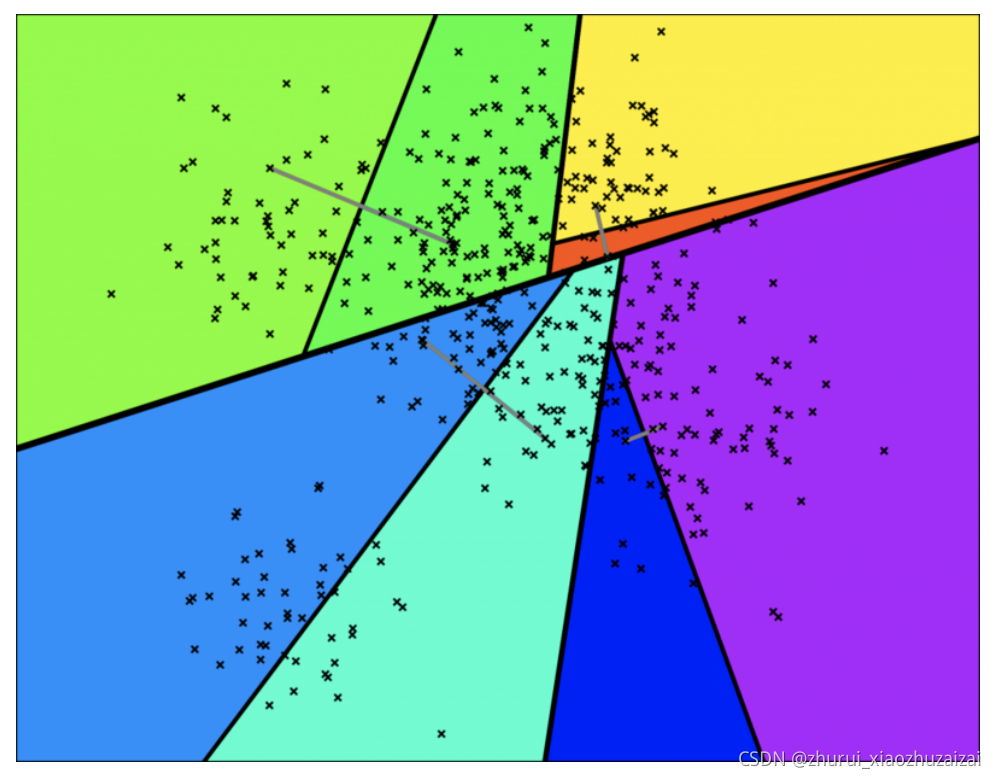
然后再继续分割，继续重复上述步骤，直到子节点包含的数据点数不超过 K 个，这里我们取 K = 10。

通过多次递归迭代划分的话，最终原始数据会形成类似下面这样一个二叉树结构。二叉树底层是叶子节点记录原始数据节点，其他中间节点记录的是分割超平面的信息。Annoy建立这样的二叉树结构是希望满足这样的一个假设: 相似的数据节点应该在二叉树上位置更接近，一个分割超平面不应该把相似的数据节点分割二叉树的不同分支上。对应的二叉树结构如下所示：

2 查询过程

通过上述步骤，我们建立了二叉树的结构用于表示上述点分布空间，每个节点都表示一个子空间，在点分布空间中接近的子空间在二叉树结构中表现为位置靠近的节点。

这里有一个假设，如果两个点在空间中彼此靠近，任何超平面都不可能将他们分开。
如果要搜索空间中的任意一个点，我们都可以从根结点遍历二叉树。
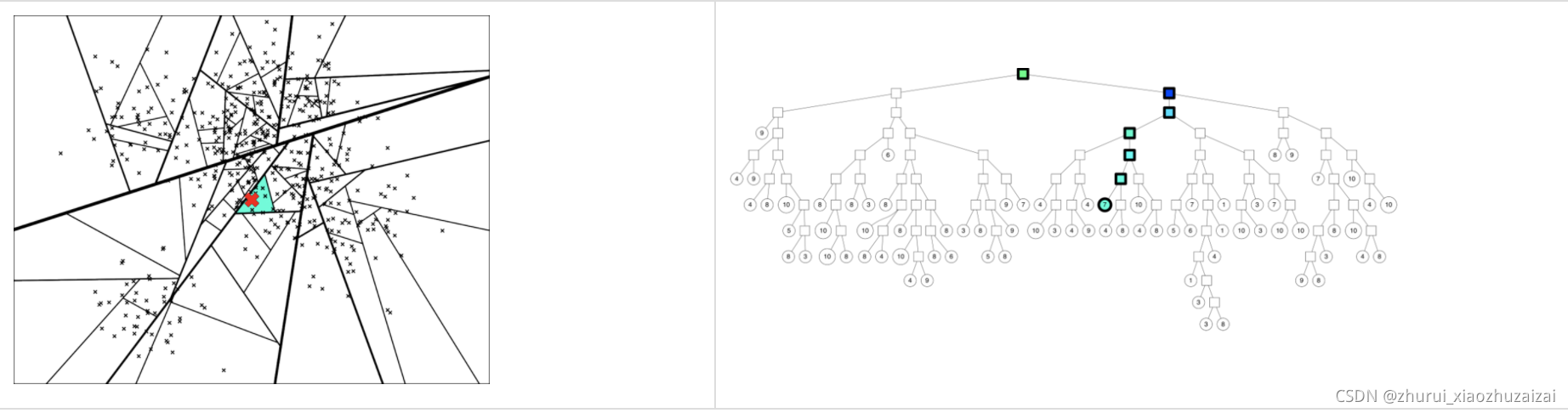
假设我们要找下图中红色 X 表示的点的临近点：查找的过程就是不断看他在分割超平面的哪一边。
从二叉树索引结构来看，就是从根节点不停的往叶子节点遍历的过程。通过对二叉树每个中间节点（分割超平面相关信息）和查询数据节点进行相关计算来确定二叉树遍历过程是往这个中间节点左孩子节点走还是右孩子节点走。
通过以上方式完成查询过程。

3 存在问题

但是上述描述存在两个问题：
（1）查询过程最终落到叶子节点的数据节点数小于 我们需要的Top N相似邻居节点数目怎么办？
（2）两个相近的数据节点划分到二叉树不同分支上怎么办？

4 解决方法

（1）如果分割超平面的两边都很相似，那可以两边都遍历；下面是是个示意图：

2） 建立多棵二叉树树，构成一个森林，每个树建立机制都如上面所述那样。多棵树示意图如下所示：

（3） 采用优先队列机制：采用一个优先队列来遍历二叉树，从根节点往下的路径，根据查询节点与当前分割超平面距离（margin）进行排序。

5:合并节点

每棵树都返回一堆近邻点后，如何得到最终的Top N相似集合呢？首先所有树返回近邻点都插入到优先队列中，求并集去重, 然后计算和查询点距离， 最终根据距离值从近距离到远距离排序， 返回Top N近邻节点集合。