说在最前面
对于大模型应用开发来说,我们可以在面试或者JD上看到,需要了解或者熟悉 模型剪枝、量化与蒸馏原理,听起来这些东西是不是比较高大上?嗯,确实挺高大上的,我们现在来说一下这几个概念和原理。
模型剪枝、量化与蒸馏,都可以认为是模型的压缩技术,先说,为什么会出现模型的压缩技术。
为什么会有模型压缩技术
如果熟悉嵌入式linux的小伙伴应该知道,嵌入式linux出现的原因,就是把能在PC端或者服务器端这种资源富余的硬件平台上的软件,比如linux操作系统,通过交叉编译、移植和内核裁剪的方式,将完整版的linux去掉一部分,直到裁剪版本的linux跑在资源相对紧张的嵌入式平台上。
模型压缩技术出现的原因也比较类似,为了降低模型的计算复杂度,减少对硬件的依赖,特别是在边缘端进行模型部署,比如手机、人脸追踪、人脸识别和特效生成的应用场景来说,算力机器有限,那么要想得到模型能力,就需要进行模型压缩。
为了在算力有限的场景上进行模型部署,需要模型压缩、优化加速、异构计算等放大突破算力限制瓶颈。这里的异构计算简单来说指的是提升设备的算力和性能。
模型压缩算法能够有效降低参数冗余,从而减少存储占用、通信带宽和计算复杂度,有助于深度学习的应用部署,对于移动端设备,计算复杂度是最重要的,因为本身移动端设备硬件条件有限,如果计算复杂度过高,会到导致模型在移动端设备跑不起来,存储占用和通信带宽想对来说不是最重要的。
模型压缩技术具体可以分为以下几种
-
线性或者非线性量化:
- 线性量化:将大模型中的权重或激活值按照固定的比例映射到有限的离散值集合中。例如,将权重值从一个连续的范围线性地映射到 8 位整数表示的范围 [-128, 127]。具体做法是先确定一个缩放因子,该因子通常根据权重或激活值的统计特性(如最大值、最小值)来计算,然后将原始值乘以缩放因子并进行舍入操作,得到量化后的整数。
- 非线性量化:根据大模型数据的分布特点,采用非均匀的量化策略。例如,对于经常出现的小数值采用较小的量化间隔,对于不常出现的大数值采用较大的量化间隔。常见的方法有基于对数变换的量化,先对数据进行对数变换,然后在变换后的空间进行均匀量化,最后再通过指数变换恢复。
通常有1/2 bits、int8和fp16等量化方式, 量化的应用价值一般是训练量化和部署量化,以前模型的原始参数一般是FP32,通过量化之后可以做到FP16,, 而现在的大模型量化 指的一般是FP32量化到 int8或者int4,量化程度很高。
-
结构或者非结构化剪枝:
- 结构化剪枝:以特定结构单元为单位对模型进行剪枝的方法。这些结构单元可以是神经元、卷积核、通道或整个层等。通过分析模型中这些结构单元的重要性,去除那些对模型性能影响较小的单元,从而达到压缩模型和提高计算效率的目的。例如,在卷积神经网络中,可以根据卷积核的权重大小或对输出的贡献度来决定是否保留该卷积核。
- 非结构化剪枝:结构化剪枝是对模型中的参数进行逐个评估和剪枝,不考虑参数的结构位置,只关注参数本身的重要性。通常根据参数的大小、梯度信息或其他度量指标来判断其对模型输出的影响,将那些不重要的参数置为零,从而实现模型压缩。例如,在全连接神经网络中,可以对每个权重参数进行单独的评估,将小于某个阈值的权重剪掉。
目前的技术一般是 deep compression, channel pruning 和 network slimming等,剪枝目前基本没有太大的商业价值
-
知识蒸馏与网络结构化
- 知识蒸馏:是一种模型压缩和迁移学习的技术,其核心思想是将一个大型、复杂且性能良好的模型(教师模型)的知识,通过某种方式传递给一个小型、简单的模型(学生模型)。教师模型通常在大规模数据集上进行了充分训练,具备丰富的知识和良好的泛化能力。知识蒸馏的过程是让学生模型学习教师模型的输出,而不仅仅是学习训练数据的标签。教师模型的输出除了最终的预测类别,还包含了类别的概率分布信息,这些信息被称为 “软标签”。学生模型通过最小化与教师模型软标签之间的差异,来学习到教师模型的知识
- 网络结构化: 网络结构化主要涉及对神经网络的结构进行设计和优化,以提高模型的性能、效率和可解释性。这包括选择合适的网络架构(如卷积神经网络、循环神经网络等)、调整网络的层数和神经元数量、引入特殊的模块(如残差块、注意力机制等)以及对网络进行剪枝、量化等操作。网络结构化的目标是使网络能够更好地提取数据特征,减少计算量和参数量,同时保持或提高模型的准确性。
包括 (squeeze-net, mobile-net,shuffle-net)等.
对于目前的阶段来说,虽然知识蒸馏属于压缩技术,但是对大模型的意义不在于压缩,而在于快速的训练大模型
剪枝
剪枝主要用于神经网络,旨在通过去除神经网络中不必要的连接、神经元或参数,来减少模型的复杂度和存储空间,同时尽量保持模型的性能。

剪枝,简单理解就是减掉模型的分支,剪枝分两种,非结构化剪枝和结构化剪枝。上图就是非结构化剪枝,剪枝前后都是4层,结构不变,而模型的参数减少,这里可以看到第二层和第三层 原本分别为4个神经元和三个神经元,剪枝之后变成3个神经元和2个神经元。对于模型来说,有极少部分参数是核心参数,起决定性作用,剪枝剪到核心参数,裁员裁到大动脉,就很尴尬了,但是你的剪枝,无法确认剪到的参数是不核心参数,简单来说,就是结果不可预估,可能剪完了之后结果很差。
剪枝的方式
-
非结构剪枝 :通常是连接级、细粒度的剪枝方法,精度想对较高,精度损失较少,但是依赖于特定的算法库或者硬件平台的支持,如果硬件不支持,那么计算量不变,精度丢失
-
结构剪枝 :是filter级或者layer级、粗粒度的剪枝方法,四层变两层,破坏了模型结构,精度想对较低,但剪枝策略更为有效,不需要特定算法库或者平台的支持,能够直接在深度学习框架上运行
-
局部方式:通过layer by layer方式、最小化输出FM重建误差的Channel Pruning, ThiNet Discrimination-aware Channel Pruning
-
全局方式 :通过训练期间对BN层 Gamma系数施加L1正约束的Network Slimming
目前一般以全局方式为主,工程上Pytorch支持剪枝支持的比较完善
我们以三个卷积,每个卷积大小为3×3×3为例对剪枝方式做说明,默认是3个蓝色的方块,每个方块有27的小方块,黄色的方块就是被剪掉的枝

Filter-level : 结构化剪枝 以前有3个核,剪完了之后变成2个核,简单,不受平台限制,精度降低
Group-level:每个核剪枝的位置都一样,固定某一层的固定某几个参数,精度比结构化高,但是依赖于硬件平台,不支持则剪枝无效
kernel-level: 第一个核剪第一层,第二个核剪上边两层,第三个核剪最下面的一层,属于层级别的剪枝。
vector-level:向量级别的剪枝,张量由向量构成,这里按照向量维度随机裁剪
fine-grained:微调剪枝,随机剪掉某个核的某个维度的某个参数,尽可能的保证剪枝的均匀化分布。剪枝最大的问题是损失明显,精度丢失较大,要想尽可能减少剪枝对模型精度的影响,那么就是随机、平均的剪,用这种方式尽可能的避免剪掉核心参数。
看起来剪枝的方式比较多,核心区别只是误差和程度上的区别,仍旧存在掉精度的问题,而且整体误差还是比较明显。
Train-Prune-Fine-tune
基于上文所描述的剪枝存在的问题,现在一般使用的剪枝方式是 Train-Prune-Fine-tune
Train-Prune-Fine-tune 的核心思想是先训练一次模型,训练之后可以了解哪些神经连接比较重要,哪些神经连接不重要,然后修剪那些不重要的神经连接,完了再次训练终于训练权重。

根据这一张图也可以很容易得看出Train-Prune-Fine-tune的策略
step1,将预训练好的模型先剪枝
step2,剪完之后,发现误差比较大,效果比较差,重新训练 retrain
step3, 训练完了之后,发现效果变好了,再剪枝
一点一点的剪枝,效果好继续剪,效果不行重新训练
看起来很完美,但是实际上,这里需要不断的剪枝->训练->剪枝->训练,而且,还不一定可以得到好的结果,因为 当某些特征以依赖于其他特征存在的方式被学习时,它们就变得 “脆弱”,对这些相互适应关系的任何破坏都可能对网络的性能产生负面影响。
简单的说
第一次剪枝效果ok,第二次剪枝不ok(因为剪多了),然后重新训练,发现训练不回去了,这就是所谓的负面影响了,这种情况就需要将 原始的参数 重新训练。
综上说,不管怎么剪枝,无法确定是不是会因为剪到大动脉导致最终的模型效果变差,你只能不断的试,结果不可控,目前的商业模型基本没有用剪枝的方式进行压缩。
写一个简单的代码来演示剪枝
虽然剪枝的弊端比较明显,但是还是写一个简单的代码说明一下剪枝,我们可以参考pytorch官网上的教程
https://pytorch.org/tutorials/intermediate/pruning_tutorial.html
我们通过如下的LetNet网络为例子

step1 打印模型可训练参数
import torch
from torch import nn
import torch.nn.utils.prune as prune
import torch.nn.functional as F
# 如果有cuda设备,比如说英伟达的显卡,那么使用cuda,否则使用cpu
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# 定义一个简单的卷积神经网络 LetNet, 具体可以参考 https://en.wikipedia.org/wiki/LeNet
# 对着上图的网络结构和代码一起看,会清晰很多
class LeNet(nn.Module):
def __init__(self):
super(LeNet, self).__init__()
# 定义第一个卷积层,输入通道数为 1,输出通道数为 6,卷积核大小为 5x5
self.conv1 = nn.Conv2d(1, 6, 5)
# 定义第二个卷积层,输入通道数为 6(注意,这里的输入是第一个卷积层的输出),输出通道数为 16,卷积核大小为 5x5。
self.conv2 = nn.Conv2d(6, 16, 5)
# 定义第一个全连接层,输入特征数为 16 * 5 * 5,输出特征数为 120(注意,这里的16是第二个卷积层的输出, 5*5是卷积层核的大小)。
self.fc1 = nn.Linear(16 * 5 * 5, 120) # 5x5 image dimension
# 定义第二个全连接层,输入特征数为 120,和第一个全连接层的输出一致,输出特征数为 84
self.fc2 = nn.Linear(120, 84)
# 定义第三个全连接层(这里是最后一个全连接层,作为模型最终输出),输入特征数为 84,输出特征数为 10,通常用于分类任务,这里假设有 10 个类别。
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
# 对第一个卷积层的输出应用 ReLU 激活函数,然后进行 2x2 的最大池化操作。
x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
# 对第二个卷积层的输出应用 ReLU 激活函数,然后进行 2x2 的最大池化操作。
x = F.max_pool2d(F.relu(self.conv2(x)), 2)
# 将卷积层的输出展平为一维向量,以便输入到全连接层。
x = x.view(-1, int(x.nelement() / x.shape[0]))
# 对全连接层fc1 fc2的输出应用 ReLU 激活函数。
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
# 通过最后一个全连接层得到最终的输出。
x = self.fc3(x)
return x
model = LeNet().to(device=device)
module = model.conv1
print(list(module.named_parameters()))
print("****")
print(list(module.named_buffers()))
输出结果如下:
[('weight', Parameter containing:
tensor([[[[ 2.8847e-02, 1.6308e-01, 7.8459e-02, 9.6718e-02, 1.4053e-01],
[-3.1480e-02, -1.9329e-01, -1.9911e-01, -5.7951e-02, 1.8997e-01],
[ 1.5439e-01, 1.4040e-03, 1.4090e-02, -8.0705e-02, 1.0796e-01],
[ 2.0710e-02, -3.5245e-02, -1.4670e-01, -1.8876e-01, 5.9700e-02],
[-2.5253e-02, 6.7459e-02, 1.4084e-01, 9.6539e-02, -9.4472e-02]]],
[[[ 1.2126e-01, 1.6421e-01, -3.7869e-02, -9.1170e-02, 3.0834e-02],
[-1.6871e-01, -7.1490e-02, 1.1854e-01, 1.3708e-01, -1.9421e-01],
[-5.2601e-02, -6.7760e-02, 1.7454e-01, 5.3142e-02, 4.6876e-03],
[ 8.8183e-02, 9.2670e-03, 1.5786e-01, 1.9395e-01, 1.5891e-01],
[ 1.6427e-01, 1.5186e-02, -1.9195e-01, -8.1249e-02, 1.9786e-01]]],
[[[ 8.4535e-02, 6.7166e-02, 2.3100e-02, 9.1294e-02, 8.0377e-02],
[-4.3604e-02, -1.1008e-02, 1.2441e-01, 1.9734e-02, 1.4928e-01],
[ 2.7477e-02, -1.5665e-01, -1.6053e-01, -4.7977e-02, 1.1194e-01],
[-7.2902e-02, 9.3897e-02, -1.8859e-01, -1.7526e-01, -4.4377e-02],
[ 1.6332e-01, -9.3463e-02, 8.9367e-02, -8.6662e-02, 1.4050e-01]]],
[[[-3.4423e-02, -5.9990e-02, -1.2821e-01, 5.2414e-02, 4.6388e-02],
[ 7.6127e-02, -8.6144e-05, -5.7394e-02, 4.3566e-02, -1.0349e-02],
[-1.6979e-01, 3.6493e-02, 1.1092e-01, -4.7735e-02, -1.1013e-01],
[ 1.9785e-01, 9.2437e-02, -4.4610e-02, 1.8850e-01, -4.3535e-02],
[ 6.2000e-02, -7.1997e-02, 4.0342e-02, 9.4967e-03, -1.6454e-01]]],
[[[ 1.6918e-01, -1.6595e-01, -9.1678e-02, -1.8477e-01, 1.7569e-01],
[-1.8553e-02, -9.5934e-02, 6.5001e-02, 1.0591e-02, -5.2795e-02],
[-1.8706e-01, -1.0165e-01, 1.2755e-01, 9.2844e-02, -1.5418e-01],
[ 8.3733e-04, -3.3268e-02, -8.1822e-02, 1.3949e-01, 5.1215e-02],
[-6.5676e-02, -7.2729e-02, -1.5418e-02, -1.0513e-01, -2.2491e-02]]],
[[[ 5.4835e-03, 6.6486e-02, -1.4393e-01, 6.0576e-02, 1.1888e-01],
[ 1.7925e-01, 8.8718e-02, -5.2512e-02, 1.4236e-01, 5.6841e-02],
[ 1.6356e-01, -7.6898e-02, -3.8401e-02, 6.9536e-02, 1.8011e-01],
[ 2.5562e-02, 1.5606e-01, 6.9030e-02, 1.0406e-01, -1.2452e-01],
[-1.9237e-01, -1.9331e-01, -1.3024e-01, 3.3731e-02, -1.2747e-01]]]],
requires_grad=True)), ('bias', Parameter containing:
tensor([ 0.1911, 0.0568, 0.1551, -0.0818, -0.0975, 0.1054],
requires_grad=True))]
****
[]
这里我们可以看到权重参数打印出来了,而模型缓存里边没有东西
step2,加上随机非结构化剪枝
# 模型结构请复制上边的代码
model = LeNet().to(device=device)
module = model.conv1
print(list(module.named_parameters()))
print("named_buffers: ****")
print(list(module.named_buffers()))
# 用于对神经网络模块进行非结构化随机剪枝操作 指定要进行剪枝的参数名称为weight,也可以是 bias
# amount 用于指定剪枝的比例或数量
# 如果 amount 是一个介于 0 到 1 之间的浮点数,它表示要将参数中 amount 比例的元素置为零。例如,amount = 0.3 表示将参数中 30% 的元素随机置为零
# 如果 amount 是一个整数,它表示要将参数中指定数量的元素置为零
# 这里是将 module 中的元素中30%置为0
prune.random_unstructured(module, name="weight", amount=0.3)
print("after random_unstructured named_parameters: ****")
print(list(module.named_parameters()))
print("after named_buffers named_parameters: ****")
print(list(module.named_buffers()))
输出结果
D:\env\python\langchain_env\python.exe "D:/env/PyCharm 2024.2.1/plugins/python-ce/helpers/pydev/pydevd.py" --multiprocess --qt-support=auto --client 127.0.0.1 --port 59462 --file G:\lession\AI2\demo\demo_16\pruning\pruning_test_01.py
已连接到 pydev 调试器(内部版本号 242.21829.153)[('weight', Parameter containing:
tensor([[[[ 0.1259, 0.1056, -0.0044, -0.0566, -0.1191],
[-0.1704, -0.0386, 0.1850, 0.1916, 0.0628],
[ 0.1035, 0.0135, 0.1306, -0.1616, 0.0801],
[-0.0570, -0.0702, -0.1025, -0.1461, -0.1081],
[ 0.0395, -0.1821, 0.1265, -0.0153, -0.1435]]],
[[[ 0.0862, -0.1205, -0.1185, -0.0739, -0.0279],
[-0.0600, 0.1785, 0.1385, 0.1838, 0.1686],
[-0.1951, -0.0297, -0.1229, 0.0650, 0.0111],
[-0.0714, -0.1751, -0.1297, -0.1336, 0.1358],
[ 0.1042, -0.0561, -0.0056, -0.1520, -0.0855]]],
[[[-0.1729, 0.1573, -0.0632, 0.0004, -0.0377],
[-0.0008, 0.1021, -0.1880, 0.1801, -0.1965],
[ 0.1121, 0.0556, 0.1849, -0.1727, -0.1362],
[ 0.1283, -0.1411, 0.1765, 0.0503, -0.1723],
[ 0.1850, 0.0229, -0.0300, -0.0165, 0.0332]]],
[[[-0.1117, 0.1264, -0.1936, -0.1620, -0.0880],
[-0.0457, -0.0659, -0.1022, -0.1281, 0.0431],
[-0.1771, 0.0860, -0.1162, -0.0766, -0.1174],
[ 0.1235, -0.0451, -0.1574, 0.0869, -0.0290],
[-0.1791, -0.1134, 0.1185, 0.1290, 0.1455]]],
[[[ 0.0773, -0.0465, -0.0746, 0.1275, -0.0199],
[-0.0007, 0.1906, -0.1434, 0.1895, 0.1852],
[-0.0071, 0.0498, 0.0186, 0.0034, -0.1598],
[ 0.1947, 0.0202, -0.1518, -0.0151, -0.0089],
[-0.0354, -0.0471, -0.0182, -0.0196, -0.0756]]],
[[[ 0.0625, -0.1876, 0.0605, -0.1334, -0.0050],
[-0.1753, -0.0958, 0.0762, -0.1613, -0.1074],
[-0.0935, -0.0596, 0.0970, 0.0934, -0.1374],
[-0.1294, -0.0456, 0.1378, -0.1242, 0.1026],
[-0.1281, 0.0311, -0.0672, -0.0548, -0.0604]]]], requires_grad=True)), ('bias', Parameter containing:
tensor([-0.0883, 0.0313, 0.0666, -0.0269, -0.0662, 0.1418],
requires_grad=True))]
named_buffers: ****
[]
after random_unstructured named_parameters: ****
[('bias', Parameter containing:
tensor([-0.0883, 0.0313, 0.0666, -0.0269, -0.0662, 0.1418],
requires_grad=True)), ('weight_orig', Parameter containing:
tensor([[[[ 0.1259, 0.1056, -0.0044, -0.0566, -0.1191],
[-0.1704, -0.0386, 0.1850, 0.1916, 0.0628],
[ 0.1035, 0.0135, 0.1306, -0.1616, 0.0801],
[-0.0570, -0.0702, -0.1025, -0.1461, -0.1081],
[ 0.0395, -0.1821, 0.1265, -0.0153, -0.1435]]],
[[[ 0.0862, -0.1205, -0.1185, -0.0739, -0.0279],
[-0.0600, 0.1785, 0.1385, 0.1838, 0.1686],
[-0.1951, -0.0297, -0.1229, 0.0650, 0.0111],
[-0.0714, -0.1751, -0.1297, -0.1336, 0.1358],
[ 0.1042, -0.0561, -0.0056, -0.1520, -0.0855]]],
[[[-0.1729, 0.1573, -0.0632, 0.0004, -0.0377],
[-0.0008, 0.1021, -0.1880, 0.1801, -0.1965],
[ 0.1121, 0.0556, 0.1849, -0.1727, -0.1362],
[ 0.1283, -0.1411, 0.1765, 0.0503, -0.1723],
[ 0.1850, 0.0229, -0.0300, -0.0165, 0.0332]]],
[[[-0.1117, 0.1264, -0.1936, -0.1620, -0.0880],
[-0.0457, -0.0659, -0.1022, -0.1281, 0.0431],
[-0.1771, 0.0860, -0.1162, -0.0766, -0.1174],
[ 0.1235, -0.0451, -0.1574, 0.0869, -0.0290],
[-0.1791, -0.1134, 0.1185, 0.1290, 0.1455]]],
[[[ 0.0773, -0.0465, -0.0746, 0.1275, -0.0199],
[-0.0007, 0.1906, -0.1434, 0.1895, 0.1852],
[-0.0071, 0.0498, 0.0186, 0.0034, -0.1598],
[ 0.1947, 0.0202, -0.1518, -0.0151, -0.0089],
[-0.0354, -0.0471, -0.0182, -0.0196, -0.0756]]],
[[[ 0.0625, -0.1876, 0.0605, -0.1334, -0.0050],
[-0.1753, -0.0958, 0.0762, -0.1613, -0.1074],
[-0.0935, -0.0596, 0.0970, 0.0934, -0.1374],
[-0.1294, -0.0456, 0.1378, -0.1242, 0.1026],
[-0.1281, 0.0311, -0.0672, -0.0548, -0.0604]]]], requires_grad=True))]
after named_buffers named_parameters: ****
[('weight_mask', tensor([[[[1., 1., 1., 1., 1.],
[0., 1., 1., 1., 1.],
[0., 0., 1., 1., 1.],
[1., 1., 1., 0., 1.],
[1., 1., 0., 0., 1.]]],
[[[0., 1., 1., 1., 1.],
[0., 0., 0., 1., 1.],
[0., 0., 1., 0., 0.],
[1., 1., 1., 1., 1.],
[1., 0., 0., 0., 1.]]],
[[[1., 1., 1., 0., 1.],
[1., 1., 1., 1., 1.],
[0., 0., 1., 0., 0.],
[1., 1., 1., 0., 1.],
[1., 1., 0., 1., 1.]]],
[[[1., 1., 1., 0., 1.],
[1., 1., 1., 0., 0.],
[1., 0., 0., 0., 1.],
[1., 0., 1., 0., 1.],
[1., 1., 0., 0., 1.]]],
[[[0., 0., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[0., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 0., 1.]]],
[[[1., 0., 1., 1., 0.],
[1., 1., 1., 1., 0.],
[1., 1., 1., 1., 1.],
[0., 0., 1., 1., 0.],
[1., 1., 1., 1., 0.]]]]))]
进程已结束,退出代码为 0
我们重点看 weight_mask 这个数组

剪枝之前模型缓存为空,剪枝之后模型缓存增加了一个 weight_mask ,这里为0表示 weight被清零,1表示不被清零,这里0占全部的30%,换句话说,这个0对应位置的参数被剪掉了。
如果不想看mask,也可以直接使用 module.weight 输出
print(module.weight)
结果如下

可以对比一下,相同位置的weight被置为了0
对于剪枝的关键方法为 prune.random_unstructured(module, name=“weight”, amount=0.3)
我们也可以使用其他的剪枝方法,例如 prune.l1_unstructured(module, name=“bias”, amount=3)
prune.l1_unstructured 函数用于对神经网络模块的参数进行非结构化剪枝。非结构化剪枝意味着剪枝操作是独立地对参数张量中的每个元素进行判断和处理,而不考虑参数的特定结构(如卷积核、通道等)。该函数基于 L1 范数(即绝对值之和)来选择要剪枝的元素,会将参数中绝对值最小的若干元素置为零,从而减少模型的复杂度和计算量
小伙伴可以使用上边的方法进行替换,并查看结果,这里就不做赘述了
剪枝可以参考如下文章
https://medium.com/@souvik.paul01/pruning-in-deep-learning-models-1067a19acd89
https://deepgram.com/learn/model-pruning-distillation-and-quantization-part-1
量化
量化是商业落地最早压缩技术,结果可控,明确的知道我应该怎么对模型进行参数量化,量化的精度和算力和存储空间 的关系是确定的,而且对精度的影响很小。
一般模型的参数都以FP32的精度存储,通过量化后得到FP16,或者INT8,甚至是INT4,以FP32需要400M显存为例,那么FP16占用200M,INT8占用100M,INT4占用50M,这样可以明显的看到 显存的要求下降非常明显,甚至可以到达数量级。
回顾量化的历史,根基权重所需要的位数,分别出现过以下的量化技术
二值神经网络:在运行时权重和激活只取两种值(例如 +1, -1)的神经网络,以及在训练时计算参数的梯度
三元权重网络:权重约束位 1,0,-1的神经网络
XNOR神经网络(异或神经网络):过滤器和卷积层数的输入是二进制的。XNOR网络主要使用二进制运算来近似卷积
基于的思路都是计算机基本都是二进制的,所以总想向着二进制方向去做,效率高,只是现实看到的效果比较尴尬,所以这三种技术都被工业淘汰了。
最终剩下的是 INT8量化部署和混合精度训练,这里需要注意的是,量化分为部署和训练两个方向。
这里进行一下说明:
对于混合精度,在模型内部参数存储的时候,模型内部会被分为两部分,参与正在计算的参数(FP32,高精度表示),和还没有参与计算的参数(FP16,低精度表示),这样可以达到的效果是,模型是16位,但是训练效果是32位的。我们比较熟悉的QLora的思想和这个是一样的,属于量化版本的混合精度训练。
INT8量化部署:FP32在推理期间被INT8取代,而训练(training)仍然是FP32。TensorRT,TensorFlow,Pytorch,MxNet和许多其他深度学习软件基本都启用量化
对于混合精度来说,因为 模型内部会被分为两部分,而且进度不一致,所以不可避免的存在量化 Quantize 和反量化 Dequantize的操作,以FP32和INT8为例,根据FP32 和INT8的转换机制,一些框架简单的引入了Quantize和Dequantize层,模型训练过程中涉及到精度转化问题,需要把8bit反量化到32bit保证模型精度,当从模型的卷积层或者全连接层送入或者取出时,它将FP32转化为INT8合作和相反。
对于训练,QLora,模型本来是16位,模型的一部分参数会转化到8bit或者4bit,这部分是不参与训练,或者是不重要的。当需要计算的时候8->16反量化。
对于推理,模型一开始就是8bit的场景,模型内部的计算也是8bit,输出也是8bit,但是这种方式不可落地,**因为AI需要接受数据,且数据不能有区别,而数据默认是32bit,但是模型是8bit的,所以数据量化操作,转成8bit。再把8bit的计算结果,在输出的时候要转成32bit,最早的思路,权重、模型内部是8bit,而数据是原有位数,这样可以兼容各种场景,但是模型全都用8bit,精度不理想。
所以现在模型的操作是,模型的参数在保存过程,一部分被保存为是8bit,另外一部分是32bit或者16bit,对于神经网络的核心或者比较重要的参数,比如说激活,被保存为精度更高的参数,这部分参数占比比较小,这里占据的算力和存储空间不高,带来的收益很高。
所以所谓的8bit/4bit是大部分非核心参数,32bit是少部分的核心参数,所以需要多次的量化和反量化。这里设计的目的是在降低模型算力依赖的前提下,尽可能的保证模型的精度结果。
量化原理
推理量化原理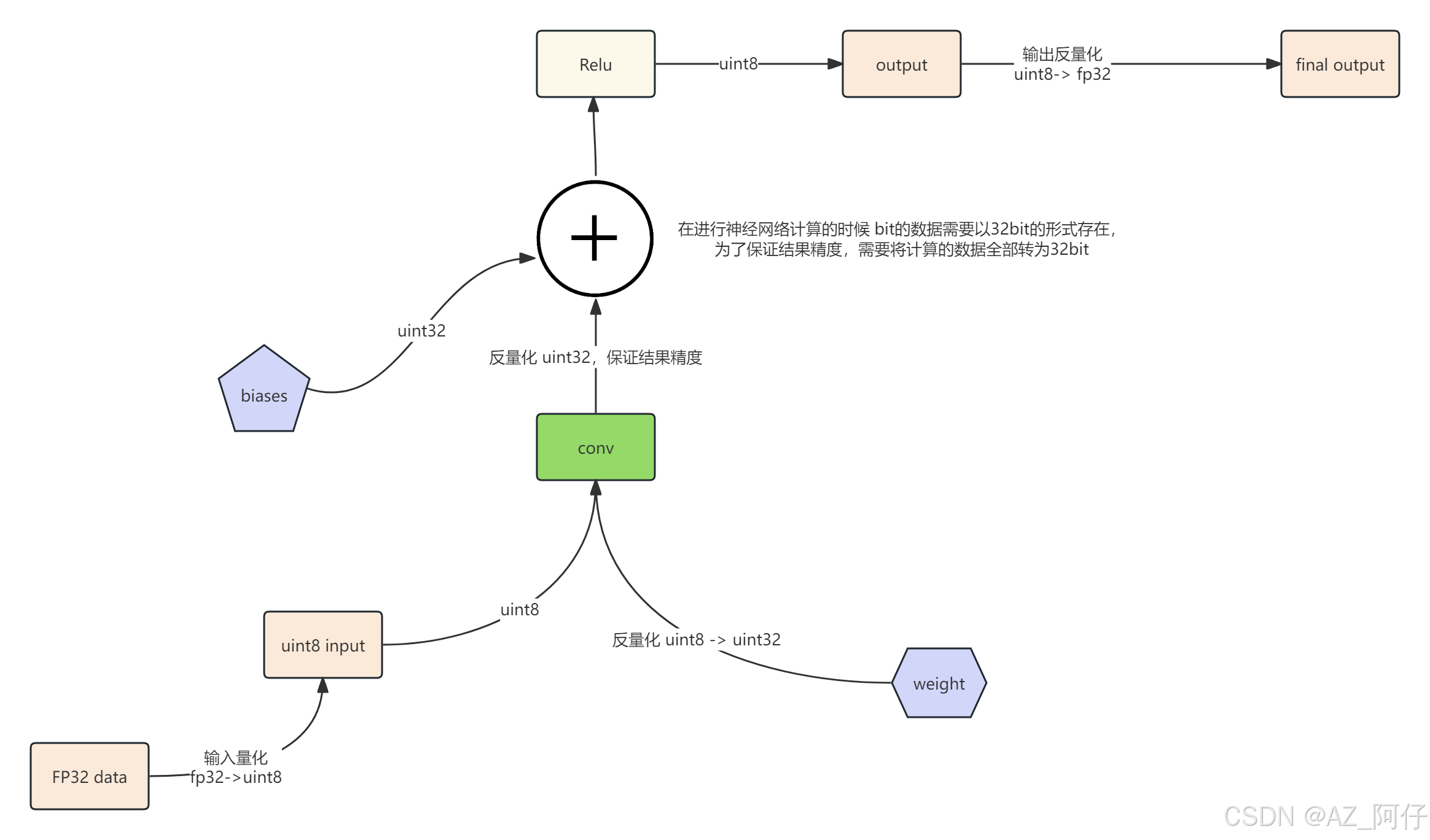
模型的权重是8bit,输入也要从32bit->8bit,这个过程是量化过程
在进行神经网络计算的时候 bit的数据需要以32bit的形式存在,为了保证结果精度,需要将计算的数据全部转为32bit
计算完成之后需要转为8bit
这里圈圈加号和 conv 指的是计算
输出的时候以32bit输出,这里最后是反量化
32bit -> 8bit(输入量化) -> 32bit(计算) -> 8bit(计算输出) -> 32 bit(输出反量化)
训练量化原理

这里和上边推理的区别是,训练的计算过程使用的是 fp32 -> int8 量化得到的低精度数据,这样可以让训练计算更快,虽然精度有丢失,但是因为是在训练过程,所以可以通过训练轮次弥补,这样的目的是节约算力和显存,这是老的方式,现在将正在参与计算的数据为32bit,而没有参与的为8bit,这样收益更高。
量化的原理:
我们一般谈LLM的精度,会涉及到FP32,FP16,BF16,INT8,INT4等字样。这些字段确定了LLM中一个参数所占的内存空间(如FP32指4字节浮点数,FP16和BF16指2字节浮点数,其中BF具有更多的指数位,INT8/4分别占8/4个比特)。其中INT8/4就涉及了模型量化,一个浮点数如何量化成一个定点数。

将数据限制到可度量的范围之内,这个数据原本可能是不可度量的,数据是由范围的(有最小值,最大值),也可能是无范围的(理论数据,无法穷举),非量化数据不可控。

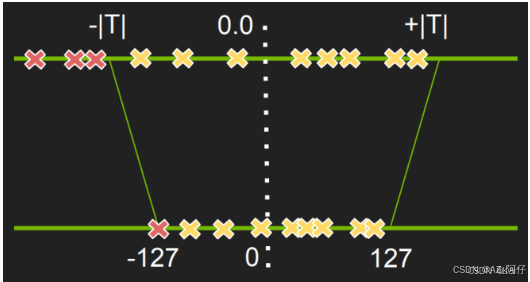
上图是有范围的[-max, max] 将数据量化到 [-127,127] ,压缩方式,用每个数据求余 127
如果是无范围,例如下图,就需要使用期望和方差,通过概率的方式取得.
本质上归一化是特殊的量化,归一化是控制在[-1,1], 而量化不一定是[-1,1]
任何的精度转化都会造成误差,但是AI计算的结果不是数值,而是趋势。量化在同一度量内做压缩,趋势是不变的。或者说比例是不变的。
100个西瓜里边有10个是熟的,和10个西瓜里边有1个是熟的,概率是一样的。
32->8 意味如果原先的模型大小为400M,那么量化之后为100M,但是低精度的丢失可能只有0.1%
通过pytorch写一个简单的量化代码
量化训练和推理实际上在各大框架例如llamafactory、deepspeed、vllm等基本都有参数可以直接配置
pytorch支持三种量化模式 Eager Mode Quantization, FX Graph Mode Quantization (maintenance) 和PyTorch 2 Export Quantization.
Eager Mode Quantization模式
先画出 量化和反量化的示意图
# original model
# all tensors and computations are in floating point
previous_layer_fp32 -- linear_fp32 -- activation_fp32 -- next_layer_fp32
/
linear_weight_fp32
# dynamically quantized model
# linear and LSTM weights are in int8
previous_layer_fp32 -- linear_int8_w_fp32_inp -- activation_fp32 -- next_layer_fp32
/
linear_weight_int8
我们通过pytorch编写代码,对简单的浮点模型进行动态量化,从而得到一个量化后的模型,并用这个量化后的模型进行推理
import torch
# 定义了一个名为 M 的自定义神经网络模块,该模块继承自 torch.nn.Module
class M(torch.nn.Module):
def __init__(self):
super().__init__()
# 创建了一个全连接层(线性层),其输入特征维度为 4,输出特征维度同样为 4。
self.fc = torch.nn.Linear(4, 4)
def forward(self, x):
# 将输入 x 传入全连接层 self.fc 进行计算。
x = self.fc(x)
return x
# 创建浮点模型实例
model_fp32 = M()
# quantize_dynamic函数用于对模型model_fp32 进行动态量化 , 得到 model_int8 的量化模型
model_int8 = torch.ao.quantization.quantize_dynamic(
model_fp32, # 传入的原始浮点模型
{torch.nn.Linear}, # 指定要进行动态量化的层类型集合,这里仅对 torch.nn.Linear 层进行量化
dtype=torch.qint8) # 指定量化后权重的数据类型为 8 位有符号整数(qint8)
# 运行模型
# input_fp32 = torch.randn(4, 4, 4, 4):生成一个形状为 (4, 4, 4, 4) 的随机张量作为输入数据。
input_fp32 = torch.randn(4, 4, 4, 4)
res = model_fp32(input_fp32)
print("model_fp32 res :" ,res)
# 将输入数据传入量化后的模型 model_int8 进行推理,得到输出结果 res
res = model_int8(input_fp32)
print("model_int8 res :" , res)
执行结果如下:
model_fp32 res : tensor([[[[ 0.3565, -0.2000, -0.4994, 0.0820],
[-0.2279, -0.3742, -0.2948, 0.2280],
[-0.2226, 0.3240, 0.0349, 0.1893],
[-0.4087, -1.0508, 0.5890, 0.0887]],
[[-0.3755, 0.4109, -0.9321, 0.0309],
[-0.0420, 0.9241, 1.2993, -0.0532],
[ 1.1547, -0.0789, 0.4885, -0.7394],
[ 0.4218, 0.1953, 0.7137, -0.3886]],
[[-0.1653, 0.6656, 0.7983, 0.0809],
[ 0.2181, -0.8939, 0.3759, 0.2098],
[-0.6793, -0.6435, 0.4489, 0.3754],
[-0.7492, -0.2926, 0.9994, 0.2567]],
[[ 2.2567, -0.3970, -0.3725, -0.0704],
[-0.1881, 0.1320, 0.2411, 0.2454],
[-0.0437, -0.4827, 0.0760, -0.3365],
[ 0.0266, 0.1265, -0.6846, -0.9112]]],
[[[ 0.4364, -1.1336, 0.0398, 0.3837],
[-0.1089, 0.5299, -0.6152, 0.7637],
[-0.3211, -0.9955, -0.1011, 0.1304],
[-0.6383, -0.5328, -0.0178, -0.4972]],
[[ 0.9327, 0.5798, -1.4510, -0.4448],
[-1.6345, 0.6200, -0.4151, 0.3484],
[ 1.1405, -0.4279, -0.1717, -0.2500],
[ 0.3051, 0.6367, 0.5340, -0.2015]],
[[-0.6563, 0.9344, -0.3421, -0.5038],
[ 0.3084, 0.3071, -0.0576, -0.4660],
[-0.5305, -0.4718, 0.4257, 0.4876],
[ 0.3400, -0.3453, 1.3450, -0.5786]],
[[ 1.0682, 0.6175, 0.0216, -0.8930],
[ 1.2664, 1.5189, 0.2069, -1.4319],
[ 1.4972, -0.4164, -0.0229, -0.8929],
[ 1.0214, 0.9937, 0.0706, -0.9203]]],
[[[ 0.5845, -0.7439, 0.6737, -0.1020],
[ 1.5555, -0.4336, 0.6417, -1.5540],
[ 0.3889, 0.4116, -0.2148, -0.3325],
[ 0.5916, -0.3409, 1.0166, -0.5657]],
[[ 0.5843, -0.3682, -0.3594, -0.0262],
[ 1.0278, -0.1169, 0.6151, 0.0651],
[ 1.6569, 0.4136, -0.3569, -1.1152],
[ 0.2567, -0.6466, 0.5466, -0.2920]],
[[ 0.0111, 0.3382, -0.1712, 0.5870],
[ 1.7966, -0.2876, 0.5484, -0.5106],
[ 0.2765, 0.2856, 1.5201, -0.6876],
[ 1.7085, -0.1518, -0.1245, -0.9372]],
[[ 0.5541, 0.7709, -0.4871, -0.5233],
[-0.2174, 0.5302, 1.2849, 0.1405],
[ 0.6776, -0.2705, 0.3988, -0.6156],
[ 0.5735, -1.6873, 0.7682, -0.3928]]],
[[[ 1.1603, -0.3293, 0.3162, -0.9144],
[ 0.1107, 0.7725, 0.3894, -0.1335],
[ 0.3665, -1.0724, 0.4536, 0.1758],
[ 0.7073, 0.0709, 0.1007, -1.1306]],
[[ 0.9111, 1.1792, -0.4199, -0.4962],
[ 0.7538, 0.0661, -0.5941, -0.4690],
[ 0.5921, -0.0428, -0.0592, 0.5561],
[ 0.5649, -1.2655, 0.3147, 0.1076]],
[[ 0.9094, 1.0980, -0.4399, -0.0375],
[ 0.9450, 0.7133, -1.0305, -1.2454],
[ 0.5015, 0.3320, -0.1408, -0.2287],
[ 0.0280, 0.3813, 0.1162, 0.7217]],
[[ 1.8927, -0.1550, -0.1346, -1.2432],
[-0.2845, -0.8825, 0.3373, 0.1608],
[-0.0470, -0.5052, 0.2978, 0.3721],
[-0.7857, 0.0376, -0.1707, -0.3394]]]], grad_fn=<ViewBackward0>)
model_int8 res : tensor([[[[ 3.5738e-01, -2.0755e-01, -4.9105e-01, 8.5995e-02],
[-2.1986e-01, -3.6999e-01, -2.8580e-01, 2.2565e-01],
[-2.2048e-01, 3.3459e-01, 1.8449e-02, 1.7884e-01],
[-4.0232e-01, -1.0547e+00, 5.8953e-01, 9.6773e-02]],
[[-3.6798e-01, 4.1035e-01, -9.3803e-01, 2.1173e-02],
[-3.8174e-02, 9.3247e-01, 1.2992e+00, -5.9201e-02],
[ 1.1580e+00, -7.7440e-02, 5.0100e-01, -7.3884e-01],
[ 4.2498e-01, 1.9771e-01, 7.0763e-01, -4.0071e-01]],
[[-1.6474e-01, 6.5901e-01, 7.8431e-01, 8.3070e-02],
[ 2.2974e-01, -8.9334e-01, 3.7613e-01, 1.9901e-01],
[-6.7655e-01, -6.2189e-01, 4.4495e-01, 3.6576e-01],
[-7.3860e-01, -2.7653e-01, 1.0009e+00, 2.5198e-01]],
[[ 2.2539e+00, -4.0048e-01, -3.7603e-01, -7.9526e-02],
[-1.8630e-01, 1.4705e-01, 2.3093e-01, 2.4536e-01],
[-4.5256e-02, -4.8932e-01, 7.0491e-02, -3.2773e-01],
[ 2.6187e-02, 1.3689e-01, -6.9845e-01, -9.0944e-01]]],
[[[ 4.4776e-01, -1.1409e+00, 3.8927e-02, 3.7916e-01],
[-1.1839e-01, 5.4322e-01, -6.2408e-01, 7.6779e-01],
[-3.3349e-01, -9.9912e-01, -9.6877e-02, 1.4297e-01],
[-6.4175e-01, -5.2181e-01, -3.2209e-02, -4.9879e-01]],
[[ 9.2955e-01, 5.9049e-01, -1.4535e+00, -4.4537e-01],
[-1.6555e+00, 6.3407e-01, -4.2315e-01, 3.5683e-01],
[ 1.1251e+00, -4.2742e-01, -1.7263e-01, -2.5028e-01],
[ 3.1550e-01, 6.4716e-01, 5.3056e-01, -2.1040e-01]],
[[-6.5684e-01, 9.3185e-01, -3.4785e-01, -4.9725e-01],
[ 3.2228e-01, 3.0826e-01, -6.5159e-02, -4.7477e-01],
[-5.3289e-01, -4.5344e-01, 4.1878e-01, 4.8401e-01],
[ 3.4660e-01, -3.5043e-01, 1.3577e+00, -5.7008e-01]],
[[ 1.0655e+00, 6.0805e-01, 3.8773e-02, -8.9096e-01],
[ 1.2724e+00, 1.5334e+00, 2.0968e-01, -1.4333e+00],
[ 1.4880e+00, -4.0941e-01, -3.4672e-02, -8.9296e-01],
[ 1.0269e+00, 9.8944e-01, 8.8968e-02, -9.1806e-01]]],
[[[ 5.8434e-01, -7.2582e-01, 6.7314e-01, -1.0416e-01],
[ 1.5585e+00, -4.4544e-01, 6.4250e-01, -1.5504e+00],
[ 3.9141e-01, 3.9972e-01, -2.1605e-01, -3.2850e-01],
[ 5.9250e-01, -3.3627e-01, 1.0151e+00, -5.6254e-01]],
[[ 5.8680e-01, -3.7199e-01, -3.4970e-01, -2.0862e-02],
[ 1.0176e+00, -1.2040e-01, 6.1987e-01, 6.4901e-02],
[ 1.6435e+00, 4.1589e-01, -3.6433e-01, -1.1111e+00],
[ 2.4683e-01, -6.4637e-01, 5.5104e-01, -2.9894e-01]],
[[ 6.2749e-04, 3.3675e-01, -1.5939e-01, 5.8240e-01],
[ 1.7824e+00, -2.9670e-01, 5.4719e-01, -5.0942e-01],
[ 2.7578e-01, 2.8778e-01, 1.5197e+00, -6.9634e-01],
[ 1.7006e+00, -1.4611e-01, -1.1813e-01, -9.4039e-01]],
[[ 5.4569e-01, 7.8096e-01, -4.9597e-01, -5.2528e-01],
[-2.1755e-01, 5.3476e-01, 1.2838e+00, 1.3696e-01],
[ 6.6702e-01, -2.6744e-01, 3.9892e-01, -6.0350e-01],
[ 5.8418e-01, -1.7023e+00, 7.7769e-01, -3.9902e-01]]],
[[[ 1.1631e+00, -3.1933e-01, 3.1454e-01, -9.2499e-01],
[ 1.1118e-01, 7.8712e-01, 3.8413e-01, -1.3850e-01],
[ 3.6816e-01, -1.0921e+00, 4.5635e-01, 1.8038e-01],
[ 7.1953e-01, 5.2051e-02, 1.0683e-01, -1.1293e+00]],
[[ 9.0984e-01, 1.1928e+00, -4.2730e-01, -5.0434e-01],
[ 7.4940e-01, 7.6533e-02, -5.9944e-01, -4.6153e-01],
[ 5.8557e-01, -3.3866e-02, -5.0223e-02, 5.5207e-01],
[ 5.6632e-01, -1.2683e+00, 3.1562e-01, 1.1571e-01]],
[[ 9.0091e-01, 1.0841e+00, -4.3131e-01, -2.3634e-02],
[ 9.5618e-01, 7.0351e-01, -1.0313e+00, -1.2423e+00],
[ 5.0289e-01, 3.2720e-01, -1.4384e-01, -2.2672e-01],
[ 2.8805e-02, 3.8617e-01, 1.0606e-01, 7.1082e-01]],
[[ 1.8785e+00, -1.5905e-01, -1.1905e-01, -1.2360e+00],
[-2.7714e-01, -8.9719e-01, 3.4041e-01, 1.5959e-01],
[-6.0962e-02, -5.0425e-01, 3.0391e-01, 3.7808e-01],
[-7.8925e-01, 4.1119e-02, -1.7848e-01, -3.3774e-01]]]])
Post Training Static Quantization 模式
Post Training Static Quantization 训练后静态量化模式 量化了模型的权重和激活。它在可能的情况下将激活融合到前面的层中。它需要使用代表性数据集进行校准,以确定激活的最佳量化参数。训练后静态量化通常是当存储器带宽和计算节省都很重要时使用的静态量化,通常用在CNN网络。
量化流程图如下
# original model
# all tensors and computations are in floating point
previous_layer_fp32 -- linear_fp32 -- activation_fp32 -- next_layer_fp32
/
linear_weight_fp32
# statically quantized model
# weights and activations are in int8
previous_layer_int8 -- linear_with_activation_int8 -- next_layer_int8
/
linear_weight_int8
代码
import torch
# 定义一个浮点模型,这个浮点模型某些层可以被静态量化
class M(torch.nn.Module):
def __init__(self):
super().__init__()
# 创建一个 QuantStub 模块,用于将浮点张量转换为量化张量。
self.quant = torch.ao.quantization.QuantStub()
# 创建一个二维卷积层,输入通道数为 1,输出通道数为 1,卷积核大小为 1x1。
self.conv = torch.nn.Conv2d(1, 1, 1)
# 创建一个 ReLU 激活函数层。
self.relu = torch.nn.ReLU()
# 创建一个 DeQuantStub 模块,用于将量化张量转换为浮点张量。
self.dequant = torch.ao.quantization.DeQuantStub()
def forward(self, x):
# 将输入张量从浮点表示转换为量化表示。
x = self.quant(x)
# 将输入数据传入卷积层进行计算。
x = self.conv(x)
# 对卷积层的输出应用 ReLU 激活函数。
x = self.relu(x)
# 将量化后的张量转换回浮点表示。
x = self.dequant(x)
return x
# 创建浮点模型实例 model_fp32
model_fp32 = M()
# 训练后静态量化模式 必须要设置模型为评估模式
model_fp32.eval()
# get_default_qconfig 获取适用于 x86 架构的默认量化配置。量化配置包含了关于如何观察激活值和权重的信息,例如使用何种量化方案(对称或非对称量化)以及校准技术(MinMax 或 L2Norm 校准)。
# model_fp32.qconfig 将获取到的量化配置应用到模型上
model_fp32.qconfig = torch.ao.quantization.get_default_qconfig('x86')
# fuse_modules 函数用于将多个模块融合为一个模块,以减少量化过程中的计算开销。这里将 conv 层和 relu 层融合在一起
model_fp32_fused = torch.ao.quantization.fuse_modules(model_fp32, [['conv', 'relu']])
# 校准模型 准备模型进行静态量化,prepare 函数用于为模型插入观察器(observers),观察器会在后续的校准过程中记录激活值的统计信息,以便确定量化参数
model_fp32_prepared = torch.ao.quantization.prepare(model_fp32_fused)
# 模型校准
# 生成一个形状为 (4, 1, 4, 4) 的随机张量作为输入数据
input_fp32 = torch.randn(4, 1, 4, 4)
# 将输入数据传入准备好的模型进行前向传播,观察器会记录激活值的统计信息,从而确定量化参数
model_fp32_prepared(input_fp32)
# 转换为量化模型 convert函数将观察后的模型转换为量化模型。它会对模型的权重进行量化,计算并存储每个激活张量的缩放因子和偏置值,同时将关键操作替换为量化实现
model_int8 = torch.ao.quantization.convert(model_fp32_prepared)
# 运行量化模型,在推理过程中,相关的计算将以 8 位整数(int8)进行,从而减少内存占用和计算量。
res = model_int8(input_fp32)
print(res)
执行结果
tensor([[[[2.6431, 1.2218, 0.4987, 1.6956],
[0.0000, 1.2966, 1.6956, 1.5210],
[1.2717, 0.0748, 2.4935, 3.1667],
[0.0499, 0.0499, 0.6483, 0.0000]]],
[[[0.8478, 0.0000, 0.3242, 1.0223],
[0.6234, 1.0223, 1.0223, 0.3491],
[2.9922, 2.0197, 1.0971, 0.2992],
[0.1995, 1.2717, 2.0945, 0.8228]]],
[[[0.6234, 1.5709, 0.8977, 0.0000],
[1.6706, 0.9475, 1.3215, 1.0971],
[0.0000, 0.1247, 1.5210, 2.8675],
[0.5236, 1.7205, 0.0249, 2.5434]]],
[[[0.7480, 0.8478, 1.3964, 1.6208],
[0.1496, 0.1995, 0.1247, 0.2992],
[0.5486, 0.9475, 0.0000, 2.8426],
[2.3439, 1.6208, 0.2992, 0.0000]]]])
量化感知训练 Quantization Aware Training for Static Quantization
量化意识训练(QAT)模拟与其他量化方法相比,训练过程中量化的效果允许更高的准确性。我们可以进行静态,动态或重量量化的QAT。在训练过程中,所有计算均在浮点状态下进行,fake_quant 模块通过逼近和舍入来模拟量化的效果,以模拟INT8的效果。在模型转换后,将重量和激活进行量化,并在可能的情况下将激活融合到前一层中。通常更适用于CNN网络,与静态量化相比,它的精度更高。
量化流程图如下
# original model
# all tensors and computations are in floating point
previous_layer_fp32 -- linear_fp32 -- activation_fp32 -- next_layer_fp32
/
linear_weight_fp32
# model with fake_quants for modeling quantization numerics during training
previous_layer_fp32 -- fq -- linear_fp32 -- activation_fp32 -- fq -- next_layer_fp32
/
linear_weight_fp32 -- fq
# quantized model
# weights and activations are in int8
previous_layer_int8 -- linear_with_activation_int8 -- next_layer_int8
/
linear_weight_int8
这里给一个简单的网络,加上模拟的数据进行训练,最后得到量化模型后进行推理
import torch
import torch.nn as nn
import torch.optim as optim
# 定义一个浮点模型,其中一些层可从量化感知训练(QAT)中受益
class M(torch.nn.Module):
def __init__(self):
super().__init__()
# QuantStub用于将张量从浮点型转换为量化型
self.quant = torch.ao.quantization.QuantStub()
# 定义一个二维卷积层,输入通道数为1,输出通道数为1,卷积核大小为1x1
self.conv = torch.nn.Conv2d(1, 1, 1)
# 定义一个二维批量归一化层,输入通道数为1
self.bn = torch.nn.BatchNorm2d(1)
# 定义一个ReLU激活函数层
self.relu = torch.nn.ReLU()
# 新增一个全局平均池化层,将特征图转换为向量,输出大小为(1, 1)
self.global_avg_pool = nn.AdaptiveAvgPool2d((1, 1))
# 新增一个全连接层,输入特征数为1,输出类别数为2
self.fc = nn.Linear(1, 2)
# DeQuantStub用于将张量从量化型转换回浮点型
self.dequant = torch.ao.quantization.DeQuantStub()
def forward(self, x):
# 将输入张量从浮点型转换为量化型
x = self.quant(x)
# 对输入张量应用卷积操作
x = self.conv(x)
# 对卷积后的张量应用批量归一化
x = self.bn(x)
# 对批量归一化后的张量应用ReLU激活函数
x = self.relu(x)
# 应用全局平均池化操作
x = self.global_avg_pool(x)
# 调整张量形状,将其展平为(batch_size, num_features)形式
x = x.view(x.size(0), -1)
# 通过全连接层得到类别分数
x = self.fc(x)
# 将张量从量化型转换回浮点型
x = self.dequant(x)
return x
# 创建一个模型实例
model_fp32 = M()
# 检查是否有可用的 CUDA 设备
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model_fp32.to(device)
# 为使模块融合操作生效,需将模型设置为评估模式
model_fp32.eval()
# 附加全局量化配置,该配置包含要附加的观察器信息。
# 对于服务器推理使用 'x86',对于移动推理使用 'qnnpack'。
# 其他量化配置(如选择对称或非对称量化以及MinMax或L2Norm校准技术)也可在此指定。
model_fp32.qconfig = torch.ao.quantization.get_default_qat_qconfig('x86')
# 在适用的情况下,将激活层与前层进行融合
# 这需要根据模型架构手动完成
model_fp32_fused = torch.ao.quantization.fuse_modules(model_fp32,
[['conv', 'bn','relu']])
# 为量化感知训练准备模型。此操作会在模型中插入观察器和伪量化节点
# 模型需设置为训练模式,以便量化感知训练逻辑生效
# 这些观察器会在校准期间观察权重和激活张量
model_fp32_prepared = torch.ao.quantization.prepare_qat(model_fp32_fused.train())
def training_loop(model, num_epochs=10, batch_size=4):
# 定义交叉熵损失函数,用于计算模型输出和真实标签之间的损失
criterion = nn.CrossEntropyLoss()
# 定义随机梯度下降(SGD)优化器,用于更新模型的参数
optimizer = optim.SGD(model.parameters(), lr=0.001, momentum=0.9)
for epoch in range(num_epochs):
running_loss = 0.0
for i in range(10): # 模拟10个批次的数据
# 生成随机输入数据,形状为(batch_size, 1, 4, 4),
# 这里在真实场景需要将输入数据转换为合适的格式,数据根据当前的网络进行预处理,得到合适的张量再进行训练
inputs = torch.randn(batch_size, 1, 4, 4).to(device)
# 生成随机标签,范围是0到1,形状为(batch_size,)
labels = torch.randint(0, 2, (batch_size,)).to(device)
# 清空优化器的梯度
optimizer.zero_grad()
# 前向传播,计算模型的输出
outputs = model(inputs)
# 计算损失
loss = criterion(outputs, labels)
# 反向传播,计算梯度
loss.backward()
# 根据计算得到的梯度更新模型参数
optimizer.step()
# 累加当前批次的损失
running_loss += loss.item()
print(f'Epoch {epoch + 1}, Loss: {running_loss / 10:.3f}')
# 运行训练循环
training_loop(model_fp32_prepared, num_epochs=10000, batch_size=4)
# 将经过训练的模型转换为量化模型。此操作会执行以下几件事:
# 对权重进行量化,计算并存储每个激活张量的缩放因子和偏差值,
# 在适当的地方融合模块,并将关键操作符替换为量化实现。
model_fp32_prepared.eval()
model_int8 = torch.ao.quantization.convert(model_fp32_prepared)
# 运行模型,相关计算将以int8类型进行
input_fp32 = torch.randn(4, 1, 4, 4).to(device)
res = model_int8(input_fp32)
print(res)
执行结果如下:
...
Epoch 96, Loss: 0.702
Epoch 97, Loss: 0.691
Epoch 98, Loss: 0.698
Epoch 99, Loss: 0.695
Epoch 100, Loss: 0.691
tensor([[-0.3969, -0.3219],
[-0.3969, -0.3437],
[-0.3969, -0.3031],
[-0.3969, -0.3062]])
因为我们使用的是随机模拟数据,所以loss不可能下降到一个可用的状态,如果需要实际应用,请自行完成数据集处理
可以参考的文档
https://zhuanlan.zhihu.com/p/548174416
https://pytorch.org/docs/stable/quantization.html
https://pytorch.org/blog/quantization-aware-training/
https://arxiv.org/pdf/1712.05877
https://zhuanlan.zhihu.com/p/64744154
https://jjjymmm.cn/index.php/archives/109/
知识蒸馏
什么是知识蒸馏?
年来,神经模型在几乎所有领域都取得了成功,包括极端复杂的问题。然而,这些模型体积巨大,有数百万(甚至数十亿)个参数,因此不能部署在边缘设备上。
知识蒸馏指的是模型压缩的思想,通过一步一步地使用一个较大的已经训练好的网络去教导一个较小的网络确切地去做什么。“软标签”指的是大网络在每一层卷积后输出的feature map。然后,通过尝试复制大网络在每一层的输出(不仅仅是最终的损失),小网络被训练以学习大网络的准确行为。


相比量化,知识蒸馏也存在不可控性,但是知识蒸馏的效果远远优于剪枝。
前提,Teacher模型的效果好,一般这种模型体量大,模型大,对数据的处理效果处理好,早期做模型部署的时候,因为太大,导致容易受限制,所以希望设计出一个小的模型,但是又能够得到大的模型的效果
所以需要有一个student 模型,参数比teacher设计更小(部署的是student模型),因为参数量的问题,导致student 在常规训练的方式得到的能力和效果永远比不上teacher。
那么有没有什么办法,让student的能力逼近teacher?有的小伙伴,有的。
让teacher带着student进行学习,teacher自己不参与训练,告诉student该怎么训练,让student自己训练。
知识蒸馏的流程
将数据集同时给到teacher和student,数据给到student之后,会得到一个常规的分类损失的输出,因为这个模型很小,所以得到的效果不好,这个时候需要借助teacher模型,数据给到teacher之后teacher可以得到一个比较接近目标的特征,这里的特征可以认为就是现实生活中的知识,具有极高的参考意义,
这时候将teacher的特征给到 student,最后让student的特征和teacher的特征进行相似度计算,简单的说student参考老师对数据的理解,并且在老师对数据理解的基础上对于数据增加了自己的理解,这个时候就有一个比较好的结果,而且中间训练速度也很快。
问题是训练的时候有两个损失,一个是teacher的,一个是student的,那么怎么处理
模型调整的时候需要参考损失,这时候student会参考teacher的损失,尤其是刚开始的时候,比较依赖老师,损失权重比刚开始是 teacher:student = 9:1, 逐步训练之后,student的能力增加,损失权重比 修改到 teacher : student = 7 : 1,再进一步学习,student能力进一步提升,损失权重比 修改到 teacher : student = 5 : 1 … 直到摆脱teacher
基于响应的知识可以用于不同类型的模型预测。例如,在目标检测任务中的响应可能包含bounding box的偏移量的logits;在人类姿态估计任务中,教师模型的响应可能包括每个地标的热力图。最流行的基于响应的图像分类知识被称为软目标(soft target)。软目标是输入的类别的概率,可以通过softmax函数估计为

Zi是第i个类别的logit,T是温度因子,控制每个软目标的重要性。软目标包含来自教师模型的暗信息知识(informative dark knowledge),
通过温度值控制不同的阶段,student模型在学习过程中对 teacher的依赖程度,随着训练的进行,T值会不断的减少,生成模型输出的就是概率分布,而学习学的也是概率分布,生成模型最大的成本在于数据,而蒸馏是一个不用标注数据的方式 的训练方式。
蒸馏也存在风险,模型的学习能力取决于模型的大小,部署需要模型足够小,所以需要蒸馏,但是模型变小之后存在风险,模型过小,学习能力不够,无法学习复杂度较大的问题,怎么学都学不会,这个时候的蒸馏就没有意义。
而对于大模型来说,关注点不是部署,而是为了能力,这个时候,如果student 不比 teacher小多少的情况下,那么蒸馏就一定有效果。
用代码解释蒸馏
import torch
from transformers import AutoTokenizer, AutoModelForCausalLM
from torch.optim import AdamW
from torch.utils.data import Dataset, DataLoader
import torch.nn.functional as F
import logging
# 配置日志记录,设置日志级别为 INFO,指定日志格式包含时间、日志级别和具体信息
logging.basicConfig(level=logging.INFO, format='%(asctime)s - %(levelname)s - %(message)s')
# ========== 配置参数 ==========
class Config:
# 模型设置,指定教师模型和学生模型的名称
teacher_model_name = "Qwen/Qwen-7B"
student_model_name = "Qwen/Qwen-1.8B"
# 训练参数
batch_size = 16 # 每个训练批次的样本数量
num_epochs = 3 # 训练的轮数
learning_rate = 2e-5 # 学习率,控制模型参数更新的步长
max_seq_length = 512 # 输入序列的最大长度
temperature = 5.0 # 蒸馏损失计算中的温度参数
alpha = 0.7 # 蒸馏损失权重,用于平衡软目标蒸馏损失和学生自训练损失
# 设备设置
device = "cuda" if torch.cuda.is_available() else "cpu" # 如果有可用的 GPU 则使用 CUDA,否则使用 CPU
grad_accum_steps = 4 # 梯度累积步数,用于模拟更大的批次大小
# 创建配置对象
config = Config()
# ========== 数据加载 ==========
class DistillationDataset(Dataset):
def __init__(self, tokenizer, sample_texts):
# 初始化分词器
self.tokenizer = tokenizer
# 用于存储处理后的样本
self.examples = []
# 遍历输入的文本样本
for text in sample_texts:
# 使用分词器对文本进行编码
encoding = tokenizer(
text,
max_length=config.max_seq_length, # 最大序列长度
padding="max_length", # 填充到最大长度
truncation=True, # 截断过长的序列
return_tensors="pt" # 返回 PyTorch 张量
)
# 将编码后的样本添加到列表中
self.examples.append(encoding)
def __len__(self):
# 返回数据集的样本数量
return len(self.examples)
def __getitem__(self, idx):
# 根据索引获取样本,并去除多余的维度
return {
"input_ids": self.examples[idx]["input_ids"].squeeze(),
"attention_mask": self.examples[idx]["attention_mask"].squeeze()
}
# ========== 模型初始化 ==========
def load_models():
try:
# 加载教师模型(冻结参数),使用预训练的模型权重,指定设备映射和数据类型
teacher = AutoModelForCausalLM.from_pretrained(
config.teacher_model_name,
device_map="auto",
torch_dtype=torch.bfloat16
).eval() # 将教师模型设置为评估模式
# 加载学生模型,使用预训练的模型权重,指定设备映射和数据类型
student = AutoModelForCausalLM.from_pretrained(
config.student_model_name,
device_map="auto",
torch_dtype=torch.bfloat16
).train() # 将学生模型设置为训练模式
return teacher, student
except Exception as e:
# 记录模型加载失败的错误信息
logging.error(f"Failed to load models: {e}")
# 抛出异常
raise
# ========== 蒸馏损失函数 ==========
class DistillationLoss:
@staticmethod
def calculate(
teacher_logits, # 教师模型的输出 logits,形状为 [batch, seq_len, vocab]
student_logits, # 学生模型的输出 logits,形状为 [batch, seq_len, vocab]
temperature=config.temperature,
alpha=config.alpha
):
# 计算软目标蒸馏损失
# 对教师模型的 logits 应用 softmax 函数,并除以温度参数
soft_teacher = F.softmax(teacher_logits / temperature, dim=-1)
# 对学生模型的 logits 应用 log_softmax 函数,并除以温度参数
soft_student = F.log_softmax(student_logits / temperature, dim=-1)
# 计算 KL 散度损失
kl_loss = F.kl_div(
soft_student,
soft_teacher,
reduction="batchmean", # 按批次求平均值
log_target=False
) * (temperature ** 2) # 乘以温度的平方
# 计算学生自训练损失(交叉熵)
# 去除学生模型 logits 的最后一个时间步
shift_logits = student_logits[..., :-1, :].contiguous()
# 取教师模型 logits 预测的标签,并去除第一个时间步
shift_labels = teacher_logits.argmax(-1)[..., 1:].contiguous()
# 计算交叉熵损失
ce_loss = F.cross_entropy(
shift_logits.view(-1, shift_logits.size(-1)),
shift_labels.view(-1)
)
# 结合软目标蒸馏损失和学生自训练损失
return alpha * kl_loss + (1 - alpha) * ce_loss
# ========== 训练流程 ==========
def train():
try:
# 初始化组件
# 加载预训练的分词器
tokenizer = AutoTokenizer.from_pretrained(config.teacher_model_name)
# 加载教师模型和学生模型
teacher, student = load_models()
# 数据集示例
sample_texts = [
"大模型的预训练过程是怎样的",
"如何评估大模型的性能优劣",
"大模型在自然语言处理中的应用场景有哪些",
"大模型的参数规模对其性能有何影响",
"大模型的训练数据需要满足什么条件",
"大模型的微调技术有哪些要点",
"大模型的推理速度如何提升",
"大模型的泛化能力是如何体现的",
"大模型的多模态融合是指什么",
"大模型在医疗领域的应用前景如何"
]
# 创建数据集对象
dataset = DistillationDataset(tokenizer, sample_texts)
# 创建数据加载器,指定批次大小
dataloader = DataLoader(dataset, batch_size=config.batch_size)
# 优化器设置,使用 AdamW 优化器,对学生模型的参数进行优化
optimizer = AdamW(student.parameters(), lr=config.learning_rate)
# 混合精度训练,使用梯度缩放器
scaler = torch.cuda.amp.GradScaler()
# 训练循环
step_count = 0 # 记录训练步数
# 将学生模型移动到指定设备
student.to(config.device)
for epoch in range(config.num_epochs):
for batch_idx, batch in enumerate(dataloader):
# 将批次数据移动到指定设备
inputs = {k: v.to(config.device) for k, v in batch.items()}
# 教师模型前向传播(不计算梯度)
with torch.no_grad(), torch.cuda.amp.autocast():
teacher_outputs = teacher(**inputs)
# 学生模型前向传播
with torch.cuda.amp.autocast():
student_outputs = student(**inputs)
# 计算蒸馏损失
loss = DistillationLoss.calculate(
teacher_outputs.logits,
student_outputs.logits
)
# 反向传播(带梯度累积)
scaler.scale(loss / config.grad_accum_steps).backward()
if (batch_idx + 1) % config.grad_accum_steps == 0:
# 梯度裁剪,防止梯度爆炸
torch.nn.utils.clip_grad_norm_(student.parameters(), 1.0)
# 参数更新
scaler.step(optimizer)
scaler.update()
optimizer.zero_grad()
step_count += 1
# 学习率调整(示例)
lr = config.learning_rate * min(step_count ** -0.5, step_count * (300 ** -1.5))
for param_group in optimizer.param_groups:
param_group['lr'] = lr
# 打印训练信息
if step_count % 10 == 0:
logging.info(f"Epoch {epoch + 1} | Step {step_count} | Loss: {loss.item():.4f}")
# 保存蒸馏后的模型
student.save_pretrained("./distilled_qwen")
tokenizer.save_pretrained("./distilled_qwen")
# 记录模型保存成功的信息
logging.info("Model saved successfully.")
except Exception as e:
# 记录训练失败的错误信息
logging.error(f"Training failed: {e}")
if __name__ == "__main__":
# 启动训练过程
train()
这里需要科学上网,保证网络通常,代码的意义请参考蒸馏原理和代码注释

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








