Hierarchical Clustering of 3D Objects and its Application to Minimum Distance Computation 阅读笔记

3D对象的层次聚类及其在最小距离计算中的应用

摘要

本文提出了一种新的迭代算法，用于自动生成复杂3D场景中包含的对象的层次聚类（hierarchical clustering of the objects）。

所提出的面向对象的表示形式比八叉树（octrees）（传统的面向场景的分层表示形式（scene-oriented hierarchical representation））具有优势。

我们的方法可以提高最小距离计算等任务的运行速度。

我们在大型合成3D场景（synthetic 3D scenes） 上进行了实验。

导论

分层表示（Hierarchical representations）

• 分层表示将复杂的问题分解成一组有层次的更简单的表示形式。
• 分层表示可以用于运动计划（motion planning）、任务组织（task organization）、图像处理（image processing）等领域。

3D层次结构（3D hierarchical structures）

• 3D层次结构可以解决碰撞检测（collision detection）、可见性分析（visibility analysis）、路径规划（path planning）等空间推理问题。
• 3D层次结构生成方法包括 面向场景（scene-oriented） 和 面向对象（object-oriented） 两种。
  • 面向场景：
    • 定义：将给定场景视为一个整体，在层次结构的每个级别上逐步细分其体积。
    • 分类：包括二元空间分区树（Binary Space Partitioning trees）、八叉树（Octress）和扩展八叉树（Extended Octrees）。
    • 不足：由于场景中包含的对象被视为场景的一部分，而不是被视为单个实体，因此许多需要处理单个对象（例如，最小距离计算）的基本任务可能会性能显著下降。
  • 面向对象：
    • 定义：关注场景中包含的单个对象，而不是整个场景。
    • 分类：包括对象内表示（intra-object representations） 和 对象间表示（intra-object representations） 两种。
      • 对象内表示 将每个单个对象分解成基本几何图元（basic geometric primitives） 的层次结构（hierarchy）。例如构造实体几何（Constructive Solid geometry，简称为CSG）就是一种基本几何图元。
      • 对象间表示 对对象进行分组。

对象间表示

A Generic Algorithm for Constructing Hierarchical Representations of Geometric Object

自底向上的启发式贪心聚类方法，将对象逐步分组为二叉树。

• 维护一个节点集合，该集合中所有节点都没有父节点。
• 对每一个节点对计算凸包，为凸包直径最小的节点对生成父节点。

Efficient Generation of Object Hierarchies from 3D Scenes

• 从全连接图中提取最小生成树（MST），保留场景中每对对象的分组成本、
• 成本函数基于万有引力定律。
• 从MST生成n元树。

优点：效率高。
缺点：随着分组的进行，成本函数缺乏更新。

例：

• 全连接图，和它的MST：
  
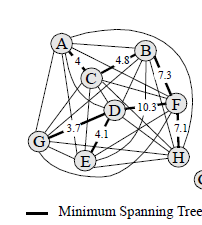
• 二元聚类树：将MST中的边根据权重递增排序，依次组合每条边连接的2个顶点。
  即：先组合G和D，然后组合A和C，然后组合GD和E，……
  缺点：太深了，因此要继续生成n元树。
  
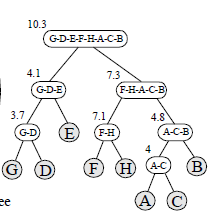
• n元树：合并可兼容的聚类
  权重最小的两条边定义$F_0$，即GDE。
  迭代地：
  • 计算$F_i$的均值${\mu }_i$和标准差${\sigma }_i$。
  • 如果某一条边的权重$w$，满足$w<{\mu }_i+2{\sigma }_i$，则将该边加入$F_i$。
  • 当没有满足条件的边时，按照相同的方法生成新的家族$F_{i+1}$。
    生成的家族为： F 0 = { 3.7 , 4 , 4.1 , 4.8 } F_0=\{3.7,4,4.1,4.8\} F0​={3.7,4,4.1,4.8}， F 1 = { 7.1 , 7.3 } F_1=\{7.1,7.3\} F1​={7.1,7.3}， F 2 = { 10.3 } F_2=\{10.3\} F2​={10.3}。
    通过合并相邻且权重边属于同一家族的聚类，生成n元图。
    

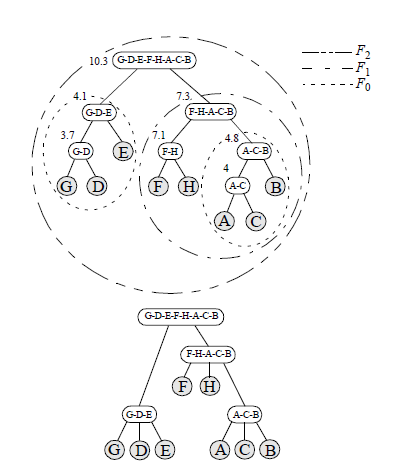
本文方法

• 定义了一个更合理直观的代价函数。
• 迭代过程。通过对前一级的 边界球（bounding sphere）（即包含所有对象的n维球）进行分组，来构建 层次结构（hierarchy） 的每一个层级（level）。当只剩单个边界球时，迭代停止。
• 包括三个阶段：
  1. 建立全连接图。每条边的权重为：在当前级别上，对该球对进行 分组（group） 的 代价（cost）。
  2. 计算该图的最小生成树MST
  3. 对MST的边基于代价进行聚类。

第一阶段：全连接图生成

以层次结构中的第 $\lambda$ 层级为例， S = { S 1 , . . . , S N } S=\{S_1,...,S_N\} S={S1​,...,SN​}是该层中出现的$N$个球。
$S_i$ 的半径为 $r_i$，3D球心为 $C_i$。

• 一开始，这些球就是他们所包含的对象的边界球
• 如果两球$S_i$和$S_j$被分组，它们将被他们的 最小边界球$S_{ij}$ 代替。

分组过程建立了一个全连接图，图中的每个节点代表了第 $\lambda$ 层级的的一个球，每条边的权重代表了将其两端的球分组的代价。

分组代价函数（grouping cost function）

背景：

• 过去使用的代价函数基于两个对象间的attraction force，或启发式地认为大小相似的两个对象应该被合并。
• 我们的方法结合两者优点，既考虑最小边界球的大小，又考虑填充因子。

填充因子（filling factor）：

• 定义： 衡量 原来的两个球 占 分组后的球（即它们的最小边界球） 的比率。（填充的程度）
• 背景： 过去的算法使用直径的比率作为填充因子，（一维）。如图，它会将a、b、c三种情况都判断为有相同的填充因子，显然是不合理的。
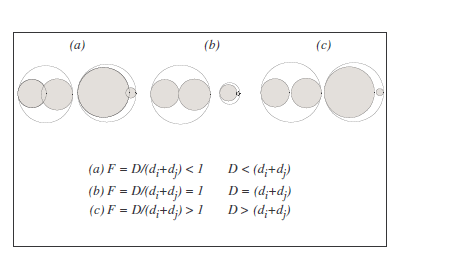
• 方法： 使用 原本两个球的体积和 与 最小边界球的体积 的 比率 作为 填充因子，是对空白空间的度量
  • 每个球$S_i$都有一个填充因子$F_i$，$F_i$可以迭代计算。$$F_{ij}=(F_{i}Vo{l}_i+F_{j}Vo{l}_j-Vo{l}_{overlap})/Vo{l}_{ij}$$

边界球大小：

• 目的： 保证分组的单调性增长。
• **方法：**使用其半径$r$进行度量。

分组代价函数：
假设球$S_i$和$S_j$的最小边界球$S_{ij}$的半径为$r_{ij}$。代价函数为：$${\zeta }_{ij}=r_{ij}^3/F_{ij}$$
两球越小越接近，分组代价函数就越小。

第二阶段：MST生成

对一个有$N$个节点和$M$条边的图。
使用Kruskal算法，可以在$O(MlogN)$的时间内生成MST。

第三阶段：对象聚类和新层级生成

• 最底层级由所有初始球组成。
• 使用X-means算法，根据分组代价，生成MST中所有边的簇。
• 新层级生成过程：根据一组簇中的边合并节点，生成的新的球与未被合并的球组成新的层级。

X-means算法

对k-means算法进行改进，但是中心点的数目是可增加的，输入给定一个中心点数目的范围，从下界开始，达到上界时终止。

X-means：

1. 执行正常的k-means算法直至收敛
2. 尝试增加新的中心点。
3. 如果中心点数目达到上界，终止算法。否则，goto 1。

两种增加中心点的方法：

• 每次分裂一个簇的中心点：
  • 选择一个簇进行分裂，在原中心点附近增加一个中心点，执行k-means算法。计算收敛后的簇集的得分，判断是否增加该中心点。
  • 时间复杂度为$O(K_{max})$，复杂度较高。
• 每次分裂所有的簇：
  • 使用一种启发式方法，每次将所有的簇都各分成两半，执行k-means算法。计算收敛后的簇集的得分，判断是否保留这些分裂。
  • 时间复杂度为$O(log{K}_{max})$，但是每次都成倍地增加簇的数目，步子迈得太大了。

本文方法：

1. 先分裂所有的簇（即使用第二种方法）。对每一个簇，将其中心点分为两个子中心点——在某一 随机方向 上 相对移动 与区域大小成比例的一段距离。
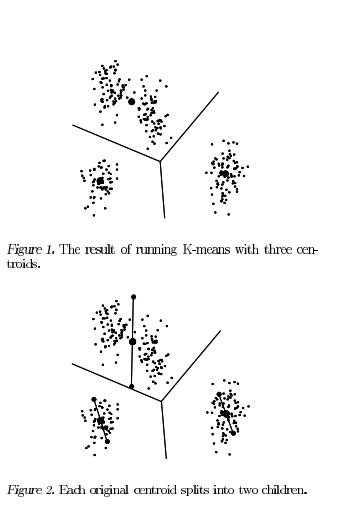
2. 对每一个父簇，以两个子中心点为初始中心点，运行一个局部的 k-means（k=2）算法，得到收敛后的结果。
   
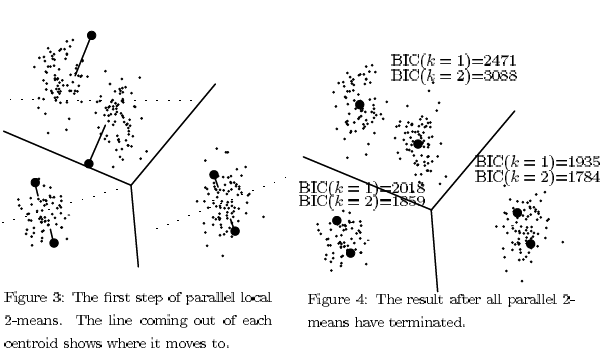
3. 判断对每一个簇所进行的分裂操作是否有意义，即获得的子模型相对父模型效果是否有提升。
   BIC Scoring
   

BIC Scoring：
贝叶斯信息量准则（Bayesian information criterion，BIC）：

• 是在有限集合中进行模型选择的准则。（越低越好）

极大似然估计（Maximum Likelihood Estimation，MLE）：

• 用于估计一个概率模型的参数。
• 给定一个概率分布$D$，已知其概率密度函数（连续分布）或概率质量函数（离散分布）为$f_D$，以及一个分布参数$\theta$ ，我们可以从这个分布中抽出一个具有$n$个值的采样$X_1,X_2,\dots ,X_n$，利用$f_D$计算出其似然函数：
  $$L(\theta \mid x_1,\dots ,x_n)=f_{\theta }(x_1,\dots ,x_n)$$
  最大似然估计会寻找关于$\theta$的最可能的值（即，在所有可能的$\theta$取值中，寻找一个值使这个采样的“可能性”最大化）。从数学上来说，我们可以在$\theta$的所有可能取值中寻找一个值使得似然函数取到最大值。这个使可能性最大的$\hat{\theta }$值即称为$\theta$的最大似然估计。

数据$D$、一系列候选模型$M_j$（不同的模型对应不同的$K$值）
使用后验概率$Pr[M_j|D]$来评价模型的得分。

假定簇中的点都符合高斯分布，求解在什么样的参数下，方差最小，满足高斯分布的概率最大。方差使用欧氏距离。
$R$是所有点的数量

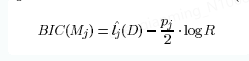
$$BIC(M_j)=\widehat{l_j}(D)-\frac{p_j}{2}\cdot \text{log}R$$
$\frac{p_j}{2}\cdot logR$是惩罚因子，对自由变量的惩罚。

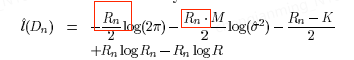
$R_n$是由${\sum }_i$求和得到的。

总结：

• $BIC(\varphi )={\hat{l}}_{\varphi }(D)-\frac{p_{\varphi }}{2}\cdot logR$
  其中：
  • $\varphi$指模型。
  • $D$指所有的数据。
  • ${\hat{l}}_{\varphi }(D)$是模型$\varphi$的最大对数似然。
  • $p_{\varphi }$是模型$\varphi$中参数的个数，作为模型复杂度的惩罚因子。
  • $R$是点的数目。
• X-Means算法假设：identical spherical assumption
  • 数据由$X$个高斯函数产生，每个高斯函数有一样的方差$\sigma$（每个维度上的变量不相关，协方差矩阵为$diag(\sigma )$）、不同的均值${\mu }_i$；
  • 数据生成时，根据概率$p_i$选择一个高斯函数$g_i$，然后生成一个点。
  • 似然函数为：
    $${\hat{l}}_{\varphi }(D)=\sum _{i=1}^R[logp(g_i)]$$

新层级生成过程

假设当前层级为$\lambda$层级。
假设 ξ = { E 0 , E 1 , . . . , E k , . . . E m } \xi=\{E_0,E_1,...,E_k,...E_m\} ξ={E0​,E1​,...,Ek​,...Em​}是当前簇中所有边的集合，且这些边按照其代价升序排列。

依次对$E_k(k=0,1,...,m)$执行以下操作，假设边$E_k$连接球$S_i$和球$S_j$：

• 如果$S_i$和$S_j$没被合并（merge）过，直接将$S_i$和$S_j$合并，使用它们的最小边界球$S_{ij}$作为一个新的对象。$S_{ij}$对应一个填充因子$F_{ij}$。
• 如果$S_i$或$S_j$已经被其他球合并过了，（将它们被合并产生的新球分别称作$S_I$和$S_J$），则计算$S_I$和$S_J$的代价${\zeta }_{IJ}$。如果${\zeta }_{IJ}\le {\zeta }_m$，则将$S_I$和$S_J$合并；否则不合并。

生成新的层级，即第$\lambda -1$层

实验

方法被用于复杂的合成3d场景。

场景层次结构

如图展示了一个包含24个对象的场景。

下图展示了该场景层次结构的每一个层级。
其中：

• 深色实心球体 表示 在之前的层级中被合并的对象。
• 深色线框球体 表示 在当前层级将要被合并的对象。
• 浅色线框球体 表示 在当前层级中不会被合并的对象。

最小距离计算

确定与 给定直线段 距离最近 的 对象。如下图所示。