使用图神经网络解决旅行商问题
由 Senem Isik 和 Michael Atkin 编写,是斯坦福 CS224W 课程项目的一部分。
旅行商问题是计算机科学中的一个经典问题,在物流和遗传学领域有着各种实际应用。在本文中,我们将展示如何使用 GNN 来解决该问题。
您是否曾梦想过踏上横跨美国的公路之旅?想象一下自己沿着 66 号公路行驶,探索国家公园,并在沿途的路边景点停留。但是,有这么多令人难以置信的目的地可供选择,规划公路旅行可能会让人感到不知所措。如何才能看到尽可能多的地方,而不会在目的地之间走回头路或曲折前行?这种情况类似于著名的旅行商问题,几十年来一直困扰着计算机科学家。

TSP 之旅将游历美国所有 49 个相邻州的一座城市。
进入图神经网络,这是一种尖端的机器学习技术,在解决这一挑战方面已显示出良好的前景。在本文中,我们将探讨这种尖端技术如何帮助您优化路线,以便您能够看到您梦想中的所有景点。
以下是这篇文章内容的概述:
- 旅行商问题的描述
- 图神经网络概述
- 图神经网络在旅行商问题中的应用
以下是我们的代码实现的链接:
谷歌合作实验室
编辑描述
colab.research.google.com
旅行商问题
旅行商问题 (TSP) 是计算机科学中的一个经典问题,它涉及寻找销售人员访问给定一组城市并返回起点的最短路线。该问题通常被表示为地图上代表城市的一组点,每对城市之间的距离已知。我们正在寻找访问每个城市一次并返回起点的路线 - 我们将这些路线称为“旅行”。目标是找到最短的旅行路线。
TSP 在现实世界中有多种应用。例如,送货司机可能需要访问一组地点来投递包裹,并希望找到最有效的路线以最大限度地减少旅行时间和燃料成本 [1]。同样,销售人员可能需要拜访一组潜在客户,并希望最大限度地减少旅行时间并最大限度地增加每天的拜访次数。TSP 也与遗传学有关,它用于分析 DNA 测序数据并确定基因出现的最可能顺序。
开发解决 TSP 的新方法至关重要,因为对于大输入量来说,它仍然是一个棘手的问题。TSP 是 NP 难问题,这意味着解决它的所有已知算法都需要指数级的时间。实际上,对于节点超过数千个的问题实例,TSP 无法得到最佳解决。最先进的 TSP 求解器将线性规划与手工启发式方法相结合以找到近似解,但对于节点超过数万个的问题实例,执行时间会变得过长 [2]。

来源:XKCD
图神经网络
图神经网络 (GNN) 是一种可以在图上运行的神经网络。GNN 可以看作是传统神经网络的泛化。传统神经网络在固定维度向量上运行,这是一种特殊的图。相反,GNN 可以在任何图上运行。为了说明这一点,请考虑您最喜欢的语言模型,例如 ChatGPT 或 PaLM。这些模型将一系列标记作为输入——换句话说,就是路径图!同样,视觉模型将像素网格作为输入——网格图!GNN 可以对所有这些类型的图进行操作,甚至更多。

左图:路径图。中图:网格图。右图:非结构化图。GNN 可以处理这三个!(来源)
GNN 非常适合解决我们的问题,因为 TSP 自然地以图的形式表示。我们可以将城市视为图中的节点。然后,该图将完全连接,每条边都包含一个正值数字,作为表示其连接的两个城市之间距离的特征。然后,我们可以简单地将问题的图形表示作为输入传递给 GNN。
其他 NP 难题求解器已通过结合神经方法提高了效率和准确性 [3] [4],因此深度学习显然有潜力改进现有的求解器。在大型图上发现 TSP 的可扩展解决方案对于物流和遗传学等领域来说将是革命性的。
最后,已经证明 GNN 训练可以学习模仿动态规划 [5]。动态规划是 TSP 等组合优化问题求解器的支柱,因此 GNN 非常适合该问题领域。
GNN 层
让我们更详细地了解一下 GNN 的工作原理。从高层次上讲,GNN 将图作为输入,该图表示为一组节点和边。GNN 的目标是学习一个函数,该函数将每个节点映射到一个向量嵌入,以捕获其结构和关系信息。

来源:CS224w讲座 3
每个GNN层由以下步骤组成:
- 消息计算:我们对每个节点的嵌入应用线性变换。这些是每个节点发送给其邻居的“消息”。
- 聚合:每个节点都会从其每个邻居接收消息。这些消息通过一些置换等变函数(例如平均值、最大值或总和)进行组合。
- 更新:更新操作获取聚合消息并更新节点表示。许多模型将在此阶段纳入额外的线性变换和残差连接。
大多数 GNN 都会堆叠多个 GNN 层。在这种情况下,前一层产生的嵌入将作为输入传递到下一层。这允许节点信息在整个图中传播多个跳跃,而不仅仅是在相邻节点之间传播。

堆叠 GNN 层的可视化。(来源)
这个基本结构抓住了 GNN 背后的关键见解——节点的表示应该受到其相邻节点的表示的影响。但是,每个步骤(消息、聚合、更新)的细节都由您决定!有各种各样的架构,它们都使用不同的消息、聚合和更新函数。其中最受欢迎的是 GCN、GraphSAGE 和 GAT。所有这些架构以及更多架构都是在 PyG 中实现的,所以请尽情尝试吧!
GNN 可以开箱即用,用于生成富有表现力的节点嵌入 - 然而,在许多情况下,GNN 被用作更大架构的一部分。这允许节点表示用于下游任务,例如节点分类、链接预测或图形聚类。
GNN 在 TSP 中的应用
数据集
对于每个 TSP 图,我们从单位正方形 [0, 1]² 中均匀采样n 个节点。为了给数据生成标签,我们使用 Concorde TSP 求解器 [2] 计算每个图的最佳路径。以下是单个训练示例的可视化:
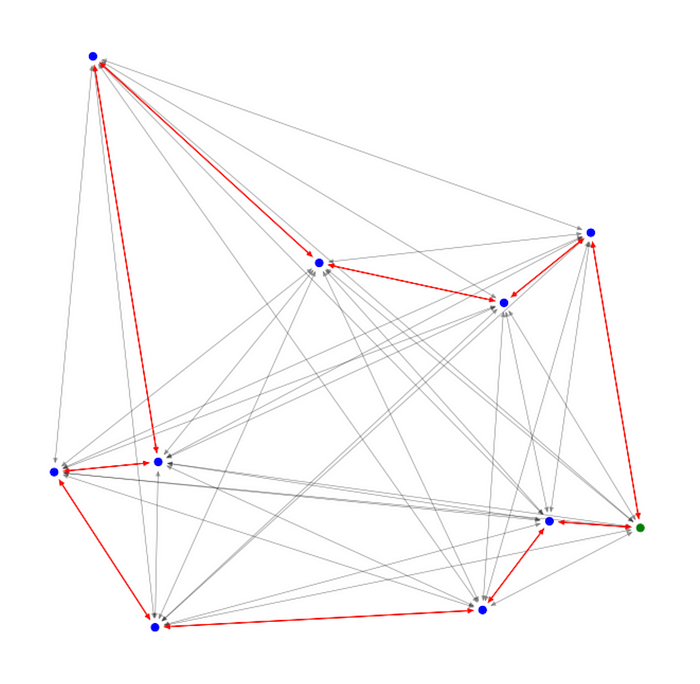
单个训练示例的可视化。蓝色节点表示城市,红色边表示最佳路线。
图变换器
我们将每个节点的输入特征定义为其 ( *x,y)*坐标。初始化之后,我们使用 Graph Transformer [6] 的一层根据以下规则获取节点嵌入:

其中注意力系数定义为:

我们将每个张量的维度设置为*(hidden_dimension, 2) ,其中**hidden_dimension*的默认值为300。
该模型已在 PyG 中完全实现!让我们来看看源代码中实现的 GNN 层的每个步骤:
- 消息计算:此步骤涉及注意系数计算,在 message() 函数下完成,定义如下:
def message(self,query_i:Tensor,key_j:Tensor,value_j:Tensor,
edge_attr:OptTensor,index:Tensor,ptr:OptTensor,
size_i:可选[ int ])->Tensor:
对于每个节点i和j,注意力系数通过以下方式计算:
alpha = (query_i * key_j).sum(dim=-1) / math.sqrt(self.out_channels)总和(dim=- 1)/math.sqrt(self.out_channels)
alpha = softmax(alpha,index,ptr,size_i)
self._alpha = alpha
alpha = F.dropout(alpha,training=self.training)
计算注意力之后,我们计算消息,然后根据其相应的注意力系数缩放每条消息。
out = value_j
out = out * alpha.view(-1, self.heads, 1)1,self.heads ,1)
返回
2.聚合:此步骤是forward()函数的一部分,定义为:
def forward(self,x:Union [Tensor,PairTensor],edge_index:Adj,
edge_attr:OptTensor = None,return_attention_weights = None):
聚合步骤由 propagate() 函数调用执行。propagate 函数由 PyG 实现,并封装了消息传递过程。它通过调用三个函数来实现这一点:1) 消息、2) 聚合和 3) 更新。我们已经在上面定义了消息函数。对于聚合,我们使用 sum 操作;对于更新,我们直接传递消息。在将节点嵌入传递到 propagate 函数调用之前,我们应用线性变换来获取注意力计算的查询、键和值。
H,C = self.heads,self.out_channels
查询=self.lin_query(x [1])。view(-1,H,C)1 ]).view(- 1 , H, C)
key = self.lin_key(x[ 0 ]).view(- 1 , H, C)
value = self.lin_value(x[ 0 ]).view(- 1 , H, C)
out = self.propagate(edge_index, query=query, key=key, value=value,
edge_attr=edge_attr, size= None )
- 更新:此步骤在 forward() 中实现。我们使用残差连接更新节点的嵌入:
x_r = self.lin_skip(x[1])1 ])
输出=输出+x_r
有关更多详细信息,请参阅源代码。请注意,了解 GNN 的内部工作原理很有用,但在实践中,PyG 会为您抽象出细节!
我们选择使用 Graph Transformer,因为它使用注意力机制,该机制在各个领域都表现出色 [7] [8]。图注意力网络 [9] 也使用注意力机制。然而,我们选择使用 Graph Transformer,因为 Shi 等人 [6] 发现 Graph Transformer 在大多数任务上的表现略优于 GAT。
残差门控 GCN
在此阶段,我们生成输入边嵌入。对于每条边,我们通过对其连接的两个节点之间的距离进行线性变换来获得其嵌入。
接下来,我们将 Graph Transformer 生成的节点嵌入和边缘特征输入到残差门控 GCN [10] 中。我们之所以选择使用残差门控 GCN,是因为它是一种简单、可扩展且经过充分研究的方法。此外,其他研究人员已将该模型应用于 TSP [11] 取得了有竞争力的成果。残差门控 GCN 的一层由以下公式表示:

残差门控 GCN 的一层。(来源)
其中每个 W 代表一个线性层,ReLU 是整流线性单元,BN 代表批量归一化。在我们的实现中,我们包括 5 个这样的层,用于解决 10 个节点的 TSP 实例。我们建议随着输入图的增大而扩展层数。
与标准 GNN 的主要区别在于,我们还会更新边嵌入。这很重要,因为我们的最终目标是预测哪些边参与了游览。除此之外,这是一个相当标准的架构。(事实上,PyG为节点嵌入实现了一个残差门控 GCN 层!)批量规范化和 ReLU 在各种深度学习学科中都表现出色。
Graph Transformers 和残差门控 GCN 之间的主要区别在于,Graph Transformer 仅更新节点嵌入,而残差门控 GCN 则同时更新节点嵌入和边嵌入。我们单独试验了这两种架构,但通过将它们结合起来,我们获得了最有力的实证结果。
后期处理
处理完所有 GNN 层后,我们在边嵌入上应用 MLP 来为每个边生成一个标量。然后,我们使用 softmax 层将这些标量转换为概率。我们的模型输出是图中每个边的概率热图,表示每个边参与最佳行程的可能性。最后,我们使用熟悉的深度学习方法:通过将模型输出与真实解进行比较来计算损失(我们使用二元交叉熵),然后通过所有模型参数反向传播损失。

我们的模型架构图。(来源)
请注意,我们的模型输出只是每条边的概率——这还不是一次有效的旅程!为了使其成为一次有效的旅程,我们需要实施搜索程序来选择将出现在我们解决方案中的边。人们可以贪婪地选择概率最高的边。然而,我们选择使用集束搜索,这是一种探索多个部分解决方案以找到最佳解决方案的算法。这是由于观察到对于许多组合优化问题,结合深度学习和搜索会产生很好的结果 [12]。
结果
评价 TSP 行程质量的标准指标是最优性差距,即模型预测的行程长度与最优行程长度之比。
然而,这意味着我们要比较应用波束搜索后的模型输出。正如 Joshi 等人 [11] 所指出的,强大的后处理搜索方法可以掩盖模型本身的缺陷。我们希望评估 GNN 层的质量,而不是搜索方法。因此,我们使用二元交叉熵直接将模型生成的概率热图与地面真实解决方案进行比较,即我们根据测试损失评估模型。
以下是我们的损失指标:
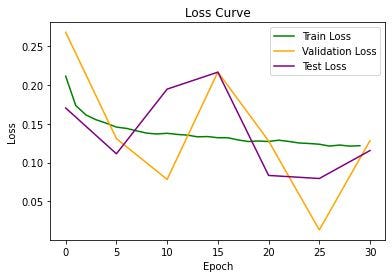
训练有些不稳定,但在第 25 个周期产生了很好的结果。在我们的实验中,我们发现无论我们使用什么架构或超参数,训练不稳定性都是一个常数。Joshi 等人也发现了类似的结果 [11]。一个有前途的研究途径是探索问题结构导致训练不稳定的原因以及如何缓解它。
洞察
以下是该模型预测的旅游行程的一些可视化效果:



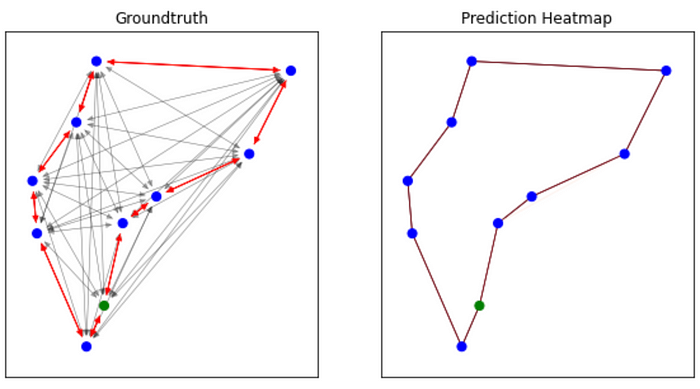
我们可以直观地观察到我们的模型能够确定最佳行程!
我们模型的主要限制在于它依赖于标记数据,这些数据是我们从 TSP 求解器获得的。如果我们希望超越 TSP 求解器的当前能力,我们就不能依赖标记训练数据。
我们可以直观地观察到我们的模型能够确定最佳行程!
我们模型的主要限制在于它依赖于标记数据,这些数据是我们从 TSP 求解器获得的。如果我们希望超越 TSP 求解器的当前能力,我们就不能依赖标记训练数据。
一个有前途的扩展是从监督学习转向强化学习。我们可以将奖励信号定义为预测的行程长度,并鼓励模型找到越来越短的行程。然后,我们可以在未标记的 TSP 图上进行训练,而无需依赖求解器。无论如何,GNN 将继续成为模型的重要组成部分,因为它们是最适合捕捉问题图结构的框架。
博客原文:专业人工智能社区























 4068
4068

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








