电磁学乱七八糟的符号(四)
@(study)[Maxe, markdown_study, LaTex_study]
author:何伟宝
这里重点是一般传输规律和矩形波导,chapter6 电磁波的传输
文章目录
纵向场量法
说白了也就是从麦克斯韦方程式抽象出我们需要的波动方程,流程如下:

矢量波动方程
在无源自由空间场量中(由麦克斯韦方程式):
(1.1)
∇
2
E
⃗
+
k
2
E
⃗
=
0
\nabla^2 \vec E+k^2\vec E=0 \tag{1.1}
∇2E+k2E=0(1.1)
(1.2)
∇
2
H
⃗
+
k
2
H
⃗
=
0
\nabla^2 \vec H+k^2\vec H=0 \tag{1.2}
∇2H+k2H=0(1.2)
在波导中,设电磁波沿着z轴传输:
(1.3)
E
⃗
(
x
,
y
,
z
)
=
E
⃗
(
x
,
y
)
e
γ
r
\vec E(x,y,z) = \vec E(x,y)e^{\gamma r } \tag{1.3}
E(x,y,z)=E(x,y)eγr(1.3)
(1.4)
H
⃗
(
x
,
y
,
z
)
=
H
⃗
(
x
,
y
)
e
γ
r
\vec H(x,y,z) = \vec H(x,y)e^{\gamma r } \tag{1.4}
H(x,y,z)=H(x,y)eγr(1.4)
其中有:
行波因子 γ \gamma γ
在上一章说过他也是一个传播常数,当 γ \gamma γ为实数时,信号衰减.虚数时信号传播,且波数为其虚部
矢量分解
这里有意地把纵横量分开了:
E
⃗
=
(
a
⃗
x
E
x
+
a
⃗
y
E
y
)
+
a
⃗
z
E
z
\vec E = (\vec a_x E_x+\vec a_y E_y) + \vec a_z E_z
E=(axEx+ayEy)+azEz
H
⃗
=
(
a
⃗
x
H
x
+
a
⃗
y
H
y
)
+
a
⃗
z
H
z
\vec H = (\vec a_x H_x+\vec a_y H_y) + \vec a_z H_z
H=(axHx+ayHy)+azHz
顺便把拉普拉斯算符
∇
\nabla
∇也分开:
∇
t
2
=
(
∂
2
∂
x
2
+
∂
2
∂
y
2
)
+
∂
2
∂
z
2
=
∇
x
y
2
+
∂
2
∂
z
2
\nabla_t^2 = (\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2})+ \frac {\partial^2}{\partial z^2}=\nabla^2_{xy}+\frac {\partial^2}{\partial z^2}
∇t2=(∂x2∂2+∂y2∂2)+∂z2∂2=∇xy2+∂z2∂2
标量波动方程
将矢量分解的三个方程先带入(1.3)(1.4)再代入(1.1)(1.2),只截取纵向分量得:
∇
x
y
2
E
⃗
z
+
(
k
2
+
γ
2
)
E
⃗
z
=
0
\nabla^2_{xy}\vec E_z+(k^2+\gamma^2)\vec E_z=0
∇xy2Ez+(k2+γ2)Ez=0
∇
x
y
2
H
⃗
z
+
(
k
2
+
γ
2
)
H
⃗
z
=
0
\nabla^2_{xy}\vec H_z+(k^2+\gamma^2)\vec H_z=0
∇xy2Hz+(k2+γ2)Hz=0
再将上式改写成(1.3)(1.4)形式:
E
z
(
x
,
y
,
z
)
=
E
z
(
x
,
y
)
E
−
γ
z
E_z(x,y,z) = E_z(x,y)E^{-\gamma z}
Ez(x,y,z)=Ez(x,y)E−γz
H
z
(
x
,
y
,
z
)
=
H
z
(
x
,
y
)
H
−
γ
z
H_z(x,y,z) = H_z(x,y)H^{-\gamma z}
Hz(x,y,z)=Hz(x,y)H−γz
考虑麦克斯韦方程的旋度式:
∇
×
E
⃗
=
−
j
ω
μ
H
⃗
\nabla \times \vec E=-j\omega \mu \vec H
∇×E=−jωμH
∇
×
H
⃗
=
j
ω
ε
E
⃗
\nabla\times\vec H =j\omega\varepsilon \vec E
∇×H=jωεE
联立上四式可得六个标量方程:
(标量1)
∂
E
z
∂
y
+
γ
E
y
=
−
j
ω
μ
H
x
\frac{\partial E_z}{\partial y}+\gamma E_y = -j\omega \mu H_x \tag{标量1}
∂y∂Ez+γEy=−jωμHx(标量1)
(标量2)
−
γ
E
x
−
∂
E
z
∂
x
=
−
j
ω
μ
H
y
-\gamma E_x -\frac{\partial E_z}{\partial x}=-j\omega \mu H_y \tag{标量2}
−γEx−∂x∂Ez=−jωμHy(标量2)
(标量3)
∂
E
y
∂
x
−
∂
E
x
∂
x
=
−
j
ω
μ
H
z
\frac{\partial E_y}{\partial x}-\frac{\partial E_x}{\partial x}=-j\omega \mu H_z \tag{标量3}
∂x∂Ey−∂x∂Ex=−jωμHz(标量3)
千万不要慌,由麦克斯韦美好的对称性可以知道,我们只要算一对叉乘就可以了,由对称性:
(标量4)
∂
H
z
∂
y
+
γ
H
y
=
j
ω
ε
E
x
\frac{\partial H_z}{\partial y}+\gamma H_y = j\omega \varepsilon E_x \tag{标量4}
∂y∂Hz+γHy=jωεEx(标量4)
(标量5)
−
γ
H
x
−
∂
H
z
∂
x
=
j
ω
ε
E
y
-\gamma H_x -\frac{\partial H_z}{\partial x}=j\omega \varepsilon E_y \tag{标量5}
−γHx−∂x∂Hz=jωεEy(标量5)
(标量6)
∂
H
y
∂
x
−
∂
H
x
∂
x
=
j
ω
ε
E
z
\frac{\partial H_y}{\partial x}-\frac{\partial H_x}{\partial x}=j\omega \varepsilon E_z \tag{标量6}
∂x∂Hy−∂x∂Hx=jωεEz(标量6)
纵横关系式
联立以上六式可得(解这个会有点痛苦,但是这不重要)纵横关系式:
(e.x)
E
x
=
−
1
k
c
2
(
γ
∂
E
z
∂
x
+
j
ω
μ
∂
H
z
∂
y
)
E_x = -\frac {1} {k_c^2}(\gamma\frac{\partial E_z}{\partial x}+j\omega\mu\frac{\partial H_z}{\partial y})\tag{e.x}
Ex=−kc21(γ∂x∂Ez+jωμ∂y∂Hz)(e.x)
(e.y)
E
y
=
−
1
k
c
2
(
γ
∂
E
z
∂
y
−
j
ω
μ
∂
H
z
∂
x
)
E_y = -\frac {1} {k_c^2}(\gamma\frac{\partial E_z}{\partial y}-j\omega\mu\frac{\partial H_z}{\partial x})\tag{e.y}
Ey=−kc21(γ∂y∂Ez−jωμ∂x∂Hz)(e.y)
(h.x)
H
x
=
−
1
k
c
2
(
γ
∂
H
z
∂
x
−
j
ω
μ
∂
E
z
∂
y
)
H_x = -\frac {1} {k_c^2}(\gamma\frac{\partial H_z}{\partial x}-j\omega\mu\frac{\partial E_z}{\partial y})\tag{h.x}
Hx=−kc21(γ∂x∂Hz−jωμ∂y∂Ez)(h.x)
(h.y)
E
x
=
−
1
k
c
2
(
γ
∂
H
z
∂
x
+
j
ω
μ
∂
E
z
∂
x
)
E_x = -\frac {1} {k_c^2}(\gamma\frac{\partial H_z}{\partial x}+j\omega\mu\frac{\partial E_z}{\partial x})\tag{h.y}
Ex=−kc21(γ∂x∂Hz+jωμ∂x∂Ez)(h.y)
其中:
k
c
2
=
k
2
+
γ
2
k_c^2=k^2+\gamma^2
kc2=k2+γ2
如果不用书本的表示方法的话,你会发现一点公式的美学…
自此,纵向常量法就介绍完成了.这里的重点在于纵横关系式
各种导波的一般传输特性
概述
这一小节解决的问题是,某种电磁波要在波导中传输的存在可能性问题.重点有TEM,TE,TM波等.并且提供假设各种波存在的时候,怎么求解波动方程的思路.
TEM横电磁波
还是回到我们熟悉的波动方程,可以把上面的纵横关系式:
(波动1)
∇
x
y
2
E
z
+
k
c
2
E
z
=
0
\nabla^2_{xy}E_z + k_c^2 E_z=0 \tag{波动1}
∇xy2Ez+kc2Ez=0(波动1)
(波动2)
∇
x
y
2
H
z
+
k
c
2
H
z
=
0
\nabla^2_{xy}H_z + k_c^2 H_z=0 \tag{波动2}
∇xy2Hz+kc2Hz=0(波动2)
显然这一节的教材安排是不合理的…因为在TEM波中:
E
z
=
0
,
H
z
=
0
E_z=0,H_z=0
Ez=0,Hz=0
显然代入纵横关系式中,全军覆没…所以分析横电磁波的时候不能采用纵向常量法得到直接表达式
这时候我们可以代入得到纵横关系式前面一点的关系式中:
(2.1)
k
c
2
=
0
或
γ
2
+
k
2
=
0
k_c^2=0\quad或\quad\gamma^2+k^2=0\tag{2.1}
kc2=0或γ2+k2=0(2.1)
(tem)
∇
x
y
2
E
⃗
(
x
,
y
)
=
0
∇
x
y
2
H
⃗
(
x
,
y
)
=
0
\nabla^2_{xy}\vec E(x,y)=0 \quad \quad \nabla^2_{xy}\vec H(x,y)=0 \tag{tem}
∇xy2E(x,y)=0∇xy2H(x,y)=0(tem)
那么我们就可以知道,代入纵横关系式会凉凉的原因是,(tem)他看上去就是一个静态场的方程,用麦克斯韦旋度式便变成0了.
这也启发我们,在求解TEM波动方程的时候,之需要先算出导波的横向分布函数,再乘以纵向传播因子 e − γ z e^{-\gamma z} e−γz就可以得到波动方程了.而且并不是每一种波导都会有TEM模.
存在条件
首先说明的一点是:空心波导只能传输TM或TE波,不能传输TEM波,因为在无外源的无限长导体空管中不可能存在静电场
书上P175,结合来看吧…(懒得打字)
TEM传播常数和相速
由(2.1)可知
γ
=
α
+
j
β
=
j
k
=
j
ω
ε
μ
\gamma=\alpha+j\beta =jk=j\omega \sqrt{\varepsilon \mu}
γ=α+jβ=jk=jωεμ
解得
α
=
0
,
β
=
ω
ε
μ
\alpha =0 \quad,\quad \beta =\omega\sqrt{\varepsilon \mu}
α=0,β=ωεμ
所以相速为:
v
=
ω
β
=
1
ε
μ
v=\frac {\omega}{\beta}=\frac1{\sqrt{\varepsilon \mu}}
v=βω=εμ1
可以看出TEM模导行波是与频率无关的非色散波
TEM的波阻抗
由(标量2)和(标量6)并代入TEM的定义式:
γ
E
x
=
j
ω
μ
H
y
\gamma E_x=j\omega \mu H_y
γEx=jωμHy
γ
H
y
=
j
ω
ε
E
x
\gamma H_y=j\omega \varepsilon E_x
γHy=jωεEx
代入
γ
=
j
ω
ε
μ
\gamma = j\omega\sqrt{\varepsilon \mu}
γ=jωεμ得(注意,求解不是联立.只要用其中一条代入就行了)
Z
T
E
M
=
E
x
H
y
=
μ
ε
=
η
Z^{TEM}=\frac{E_x}{H_y}=\sqrt{\frac{\mu}{\varepsilon}}=\eta
ZTEM=HyEx=εμ=η
可以看出,
Z
T
E
M
Z^{TEM}
ZTEM和频率是没有关系的.
所以:TEM模在任何频率下都能传播非色散横电磁波
TE nor TM
在TM波中,
E
z
≠
0
E_z \neq 0
Ez̸=0和
H
z
=
0
H_z=0
Hz=0.所以只需要代入(波动1),同理:
在TE波中,
H
z
≠
0
H_z \neq 0
Hz̸=0和
E
z
=
0
E_z=0
Ez=0.所以只需要代入(波动2)
存在条件
可以看出,无论是哪一种,
k
c
2
k_c^2
kc2都不会等于0,所以:
γ
2
+
k
2
≠
0
\gamma^2+k^2 \neq 0
γ2+k2̸=0
被称为波导中TM波和TE波的存在条件。
传播常数和截止频率
由传播因子
e
−
j
γ
z
e^{-j\gamma z}
e−jγz可以知道,在
e
−
γ
z
→
0
e^{-\gamma z}\to 0
e−γz→0时,传播截止.这个时候有
γ
→
1
\gamma \to 1
γ→1
所以有:
γ
=
k
c
2
−
ω
c
2
ε
μ
=
0
\gamma=\sqrt{k^2_c-\omega_c^2 \varepsilon \mu}=0
γ=kc2−ωc2εμ=0
解得:
f
c
=
k
c
2
π
ε
μ
f_c=\frac{k_c}{2\pi\sqrt{\varepsilon\mu}}
fc=2πεμkc
其中,
f
c
f_c
fc被称为截止频率或临界频率(c to cut),所以反过来求
γ
\gamma
γ得:
γ
=
{
j
k
1
−
(
f
c
f
)
2
=
j
β
f
>
f
c
k
c
1
−
(
f
c
f
)
2
=
α
f
<
f
c
\gamma=\begin{cases} jk\sqrt{1-(\frac{f_c}{f})^2}= j\beta \quad f>f_c \\k_c\sqrt{1-(\frac{f_c}{f})^2}=\alpha\quad f<f_c \end{cases}
γ=⎩⎨⎧jk1−(ffc)2=jβf>fckc1−(ffc)2=αf<fc
可以看出:
当
f
<
f
c
f<f_c
f<fc时,传播因子变成了
e
−
α
z
e^{-\alpha z}
e−αz,是一个衰减型凋落场
当
f
>
f
c
f>f_c
f>fc时,传播因子变成了
e
−
j
β
z
e^{-j\beta z}
e−jβz,表示一个传播型色散行波
相速和波导波长
当
f
>
f
c
f>f_c
f>fc时,因为是一个色散波,我们可以来讨论一下他的相速,由上面:
β
=
k
1
−
(
f
c
f
)
2
\beta=k\sqrt{1-(\frac{f_c}{f})^2}
β=k1−(ffc)2
所以有,相速:
v
p
=
ω
β
=
v
1
−
(
f
c
f
)
2
>
v
v_p=\frac\omega\beta=\frac{v}{\sqrt{1-(\frac{f_c}{f})^2}}>v
vp=βω=1−(ffc)2v>v
波导内波导行波的波长称为波导波长:
λ
g
=
2
π
β
=
2
π
k
1
1
−
(
f
c
f
)
2
=
λ
1
−
(
f
c
f
)
2
>
λ
\lambda_g=\frac{2\pi}{\beta}=\frac{2\pi}{k}\frac1{\sqrt{1-(\frac{f_c}{f})^2}}=\frac\lambda{\sqrt{1-(\frac{f_c}{f})^2}} >\lambda
λg=β2π=k2π1−(ffc)21=1−(ffc)2λ>λ
表明导行波是与频率有关的色散行波
波阻抗
TM波
由纵横关系式,结合tm波的特征可得:
E
x
=
−
γ
k
c
2
∙
∂
E
z
∂
x
E_x=-\frac{\gamma}{k_c^2}\bullet\frac{\partial E_z}{\partial x}
Ex=−kc2γ∙∂x∂Ez
E
y
=
−
γ
k
c
2
∙
∂
E
z
∂
y
E_y=-\frac{\gamma}{k_c^2}\bullet\frac{\partial E_z}{\partial y}
Ey=−kc2γ∙∂y∂Ez
H
x
=
j
ω
ε
k
c
2
∙
∂
E
z
∂
y
H_x=\frac{j\omega\varepsilon}{k_c^2}\bullet\frac{\partial E_z}{\partial y}
Hx=kc2jωε∙∂y∂Ez
E
y
=
−
j
ω
ε
k
c
2
∙
∂
E
z
∂
x
E_y=-\frac{j\omega\varepsilon}{k_c^2}\bullet\frac{\partial E_z}{\partial x}
Ey=−kc2jωε∙∂x∂Ez
所以定义TM波的波阻抗为:
Z
T
M
=
E
x
H
y
=
−
E
y
H
x
=
γ
j
ω
ε
Z^{TM}=\frac{E_x}{H_y}=\frac{-E_y}{H_x}=\frac{\gamma}{j\omega\varepsilon}
ZTM=HyEx=Hx−Ey=jωεγ
消去
γ
\gamma
γ得:
Z
T
M
=
{
η
1
−
(
f
c
f
)
2
=
R
T
M
,
f
>
f
c
−
j
k
c
ω
ε
1
−
(
f
c
f
)
2
=
−
j
X
c
T
M
,
f
<
f
c
Z^{TM}=\begin{cases}\eta\sqrt{1-(\frac{f_c}{f})^2} =R^{TM},\quad \quad\quad\quad f>f_c \\-j\frac{k_c}{\omega\varepsilon}\sqrt{1-(\frac{f_c}{f})^2}=-jX_c^{TM}, \quad f<f_c \end{cases}
ZTM=⎩⎨⎧η1−(ffc)2=RTM,f>fc−jωεkc1−(ffc)2=−jXcTM,f<fc
TE波
按照TM波的套路,代入
E
z
=
0
E_z=0
Ez=0得:
Z
T
M
=
{
η
1
1
−
(
f
c
f
)
2
=
R
T
E
,
f
>
f
c
j
μ
ω
k
c
1
1
−
(
f
c
f
)
2
=
j
X
c
T
E
,
f
<
f
c
Z^{TM}=\begin{cases}\eta\frac1{\sqrt{1-(\frac{f_c}{f})^2}} =R^{TE},\quad \quad\quad\quad f>f_c \\j\frac{\mu\omega}{k_c}\frac1{\sqrt{1-(\frac{f_c}{f})^2}}=jX_c^{TE},\quad \quad \quad f<f_c \end{cases}
ZTM=⎩⎪⎨⎪⎧η1−(ffc)21=RTE,f>fcjkcμω1−(ffc)21=jXcTE,f<fc
互易性
由上面可以得出:
Z
T
M
∙
Z
T
E
=
η
2
=
(
Z
T
E
M
)
2
Z^{TM}\bullet Z^{TE}=\eta^2 =(Z^{TEM})^2
ZTM∙ZTE=η2=(ZTEM)2
可以看到TE和TM波的波阻抗具有互易性
矩形波导
这里也是要做纵横关系式求解的最后一步,代入边界条件
由前面就可以知道,矩形波导不能传播TEM波
首先假设矩形波导的数学模型:

长a宽b壁导体
先上一张图辅助一下大家后面看边界条件的法向还是切向
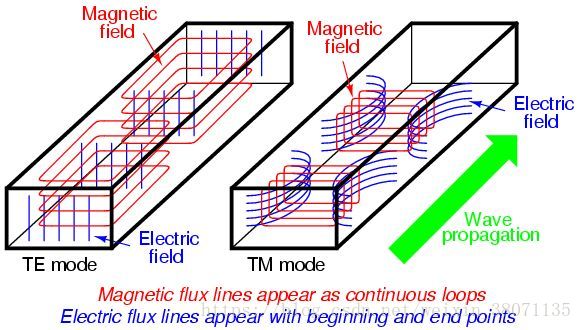
TM(图的右边)
边界条件:
(
∂
2
∂
x
2
+
∂
2
∂
y
2
+
k
c
2
)
E
z
(
x
,
y
)
=
0
(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+k_c^2)E_z(x,y)=0
(∂x2∂2+∂y2∂2+kc2)Ez(x,y)=0
{
E
z
∣
x
=
0
=
0
,
E
z
∣
x
=
a
=
0
E
z
∣
y
=
0
=
0
,
E
z
∣
y
=
b
=
0
\begin{cases}E_z|_{x=0}=0,\quad E_z|_{x=a}=0 \\ E_z|_{y=0}=0,\quad E_z|_{y=b}=0\end{cases}
{Ez∣x=0=0,Ez∣x=a=0Ez∣y=0=0,Ez∣y=b=0
其中
k
c
2
=
γ
2
+
k
2
k_c^2=\gamma^2+k^2
kc2=γ2+k2称为截止波数.
公式的意义是很明确的:
传播TM波的时候矩形波导的边界都没有电场强度
以下是我以为的原因(有异议可以评论,大家互相学习一下)
- 一个原因(一对边)在于,边界条件中,法向的电场强度连续,而理想导体内部没有电磁场
- 另一对边是因为,上一章说过的趋肤效应导致的,而由于是 σ = ∞ \sigma=\infty σ=∞所以就为0了
纵向解
由于我们想求的纵横关系式中,x和y是独立分开的.所以假设:
E
z
(
x
,
y
)
=
X
(
x
)
Y
(
y
)
E_z(x,y)=X(x)Y(y)
Ez(x,y)=X(x)Y(y)
代入波动方程并化成常微分方程得:
d
2
X
d
x
2
+
k
x
2
X
=
0
\frac {d^2 X}{dx^2}+k_x^2 X=0
dx2d2X+kx2X=0
d
2
Y
d
x
2
+
k
y
2
Y
=
0
\frac {d^2 Y}{dx^2}+k_y^2 Y=0
dx2d2Y+ky2Y=0
其中:
k
c
2
=
k
x
2
+
k
y
2
\quad \quad k_c^2=k_x^2+k^2_y
kc2=kx2+ky2
显然特征方程的根是两个纯虚数,故设通解:
X
(
x
)
=
A
s
i
n
k
x
x
+
B
c
o
s
k
x
x
X(x)=Asink_x x +Bcosk_x x
X(x)=Asinkxx+Bcoskxx
Y
(
y
)
=
C
s
i
n
k
y
y
+
D
c
o
s
k
y
y
Y(y)=Csink_y y +Dcosk_y y
Y(y)=Csinkyy+Dcoskyy
分别代入边界条件可得(书上P176):
E
z
(
x
,
y
)
=
E
0
s
i
n
m
π
a
x
s
i
n
n
π
b
y
,
m
,
n
=
1
,
2
,
3......
E_z(x,y)=E_0 sin\frac{m\pi}{a}x sin \frac{n\pi}{b}y,\quad m,n=1,2,3......
Ez(x,y)=E0sinamπxsinbnπy,m,n=1,2,3......
其中:
E
0
=
A
C
\quad\quad \quad E_0=AC
E0=AC由激励源强度确定
大概的思路是先带入x=0和y=0那两条,算出B,D=0再代入剩下两条即可.
横向解
现在求出了
E
z
E_z
Ez的表达式,显然,代入一般情况可得:
E
x
=
−
γ
k
c
2
(
m
π
a
)
E
0
c
o
s
m
π
a
x
s
i
n
n
π
b
y
E_x=-\frac{\gamma}{k_c^2}(\frac{m\pi}{a})E_0 cos\frac{m\pi}{a}xsin\frac{n\pi}{b}y
Ex=−kc2γ(amπ)E0cosamπxsinbnπy
E
y
=
−
γ
k
c
2
(
n
π
b
)
E
0
s
i
n
m
π
a
x
s
i
n
n
π
b
y
E_y=-\frac{\gamma}{k_c^2}(\frac{n\pi}{b})E_0 sin\frac{m\pi}{a}xsin\frac{n\pi}{b}y
Ey=−kc2γ(bnπ)E0sinamπxsinbnπy
H
x
=
j
ω
ε
k
c
2
(
n
π
b
)
E
0
s
i
n
m
π
a
x
c
o
s
n
π
b
y
H_x=\frac{j\omega\varepsilon}{k_c^2}(\frac{n\pi}{b})E_0 sin\frac{m\pi}{a}xcos\frac{n\pi}{b}y
Hx=kc2jωε(bnπ)E0sinamπxcosbnπy
H
y
=
j
ω
ε
k
c
2
(
m
π
a
)
E
0
s
i
n
n
π
b
x
c
o
s
m
π
a
y
H_y=\frac{j\omega\varepsilon}{k_c^2}(\frac{m\pi}{a})E_0 sin\frac{n\pi}{b}xcos\frac{m\pi}{a}y
Hy=kc2jωε(amπ)E0sinbnπxcosamπy
其中:
k
c
=
γ
2
+
k
2
=
k
x
2
+
k
y
2
=
(
m
π
a
)
2
+
(
n
π
b
)
2
k_c=\sqrt{\gamma^2+k^2}=\sqrt{k_x^2+k_y^2}=\sqrt{(\frac{m\pi}{a})^2+(\frac{n\pi}{b})^2}
kc=γ2+k2=kx2+ky2=(amπ)2+(bnπ)2
由TE,TM的存在条件可以知道,当m=n=0时,方程无意义
TE(图的左边)
由于和TM是同一个套路,这里就直接给公式了:
边界条件
(
∂
2
∂
x
2
+
∂
2
∂
y
2
+
k
c
2
)
H
z
(
x
,
y
)
=
0
(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+k_c^2)H_z(x,y)=0
(∂x2∂2+∂y2∂2+kc2)Hz(x,y)=0
{
H
z
∣
x
=
0
=
0
,
H
z
∣
x
=
a
=
0
H
z
∣
y
=
0
=
0
,
H
z
∣
y
=
b
=
0
\begin{cases}H_z|_{x=0}=0,\quad H_z|_{x=a}=0 \\ H_z|_{y=0}=0,\quad H_z|_{y=b}=0\end{cases}
{Hz∣x=0=0,Hz∣x=a=0Hz∣y=0=0,Hz∣y=b=0
纵向解
H z ( x , y ) = H 0 c o s m π a x c o s n π b y , m , n = 1 , 2 , 3...... H_z(x,y)=H_0 cos\frac{m\pi}{a}x cos\frac{n\pi}{b}y,\quad m,n=1,2,3...... Hz(x,y)=H0cosamπxcosbnπy,m,n=1,2,3......
横向解
E
x
=
j
ω
ε
k
c
2
(
n
π
b
)
H
0
c
o
s
m
π
a
x
s
i
n
n
π
b
y
E_x=\frac{j\omega\varepsilon}{k_c^2}(\frac{n\pi}{b})H_0 cos\frac{m\pi}{a}xsin\frac{n\pi}{b}y
Ex=kc2jωε(bnπ)H0cosamπxsinbnπy
E
y
=
−
j
ω
ε
k
c
2
(
m
π
a
)
H
0
s
i
n
m
π
a
x
c
o
s
n
π
b
y
E_y=-\frac{j\omega\varepsilon}{k_c^2}(\frac{m\pi}{a})H_0 sin\frac{m\pi}{a}xcos\frac{n\pi}{b}y
Ey=−kc2jωε(amπ)H0sinamπxcosbnπy
H
x
=
γ
k
c
2
(
m
π
a
)
H
0
c
o
s
n
π
b
y
s
i
n
m
π
b
x
H_x=\frac{\gamma}{k_c^2}(\frac{m\pi}{a})H_0 cos\frac{n\pi}{b}ysin\frac{m\pi}{b}x
Hx=kc2γ(amπ)H0cosbnπysinbmπx
H
y
=
γ
k
c
2
(
n
π
b
)
H
0
s
i
n
m
π
a
x
s
i
n
n
π
b
y
H_y=\frac{\gamma}{k_c^2}(\frac{n\pi}{b})H_0 sin\frac{m\pi}{a}xsin\frac{n\pi}{b}y
Hy=kc2γ(bnπ)H0sinamπxsinbnπy
同理:m=n=0时,公式无意义
横场分布的物理特性
这里对应的是P178,下面列举出来只作复习回想用:
- 沿x,y的驻波性和z向的行波性
- 平面波的非均匀性
- 场的多模性
- 模式的兼并性
- 模式的阶次性
导波的纵场传输特性*
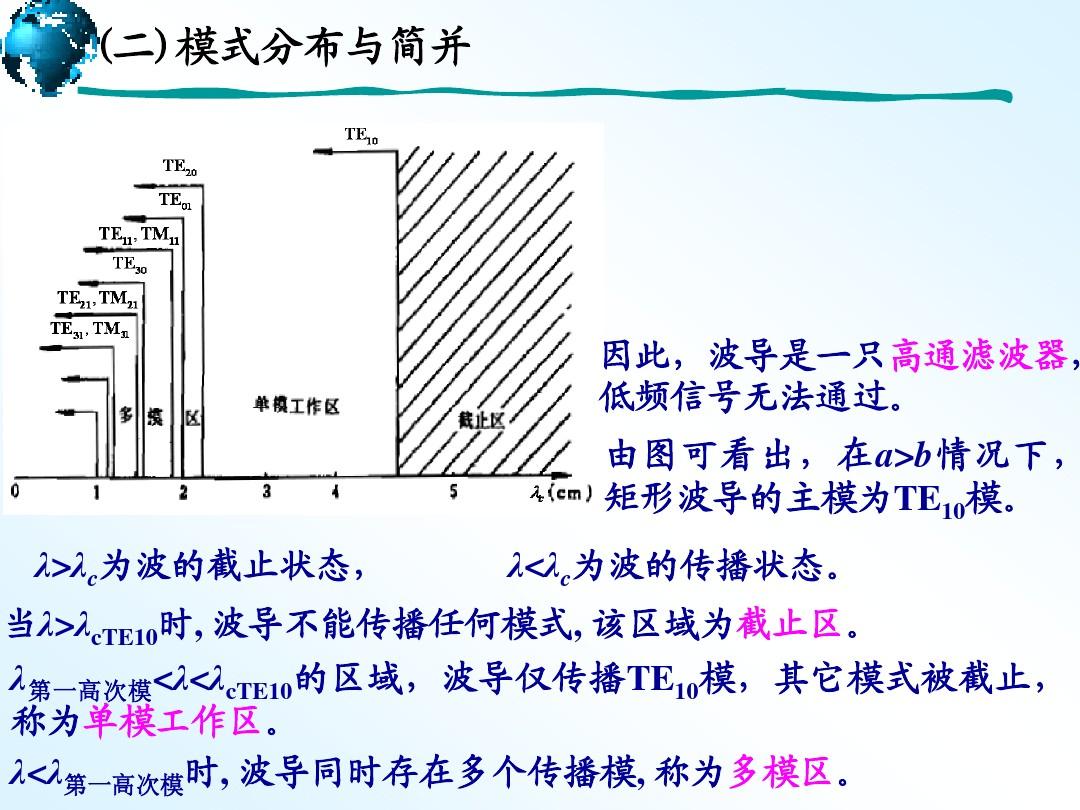
截止性(高通特性)
之前在一般传输特性就讲过这个问题,只是k可以由m和n给出,所以回代得:
k
c
=
γ
2
+
k
2
=
k
x
2
+
k
y
2
=
(
m
π
a
)
2
+
(
n
π
b
)
2
k_c=\sqrt{\gamma^2+k^2}=\sqrt{k_x^2+k_y^2}=\sqrt{(\frac{m\pi}{a})^2+(\frac{n\pi}{b})^2}
kc=γ2+k2=kx2+ky2=(amπ)2+(bnπ)2
f
c
−
k
c
2
π
ε
μ
=
1
2
ε
μ
(
m
a
)
2
+
(
n
b
)
2
f_c-\frac{k_c}{2\pi \sqrt{\varepsilon\mu}}=\frac1{2\sqrt{\varepsilon\mu}}\sqrt{(\frac ma)^2+(\frac nb)^2}
fc−2πεμkc=2εμ1(am)2+(bn)2
λ
c
=
2
π
k
c
=
2
(
m
a
)
2
+
(
n
b
)
2
\lambda_c=\frac{2\pi}{k_c}=\frac2{\sqrt{(\frac ma)^2+(\frac nb)^2} }
λc=kc2π=(am)2+(bn)22
色散性和滤波性
由上一个性质可以知道,在截取频率之前的波形都会因为传播常数的实部不为0而全部被去掉
所以当f>
f
c
f_c
fc时(
α
=
0
\alpha=0
α=0):
β
=
ω
2
ε
μ
−
(
m
π
a
)
2
−
(
n
π
b
)
2
\beta=\sqrt{\omega^2\varepsilon\mu-(\frac{m\pi}{a})^2-(\frac{n\pi}{b})^2}
β=ω2εμ−(amπ)2−(bnπ)2
λ
g
=
2
π
β
=
2
π
ω
2
ε
μ
−
(
m
π
a
)
2
−
(
n
π
b
)
2
\lambda_g=\frac{2\pi}{\beta}=\frac{2\pi}{\sqrt{\omega^2\varepsilon\mu-(\frac{m\pi}{a})^2-(\frac{n\pi}{b})^2}}
λg=β2π=ω2εμ−(amπ)2−(bnπ)22π
v
p
=
ω
β
=
ω
ω
2
ε
μ
−
(
m
π
a
)
2
−
(
n
π
b
)
2
v_p=\frac{\omega}{\beta}=\frac{\omega}{\sqrt{\omega^2\varepsilon\mu-(\frac{m\pi}{a})^2-(\frac{n\pi}{b})^2}}
vp=βω=ω2εμ−(amπ)2−(bnπ)2ω
阻抗双重性
这个由截止性就知道,低于截止频率的波阻抗呈阻性,高于的呈电抗性:
Z
T
M
=
γ
j
ω
ε
=
{
1
ω
ε
ω
2
ε
μ
−
(
m
π
a
)
2
−
(
n
π
b
)
2
=
R
T
M
,
f
>
f
c
−
j
1
ω
ε
(
m
π
a
)
2
+
(
n
π
b
)
2
−
ω
2
ε
μ
=
−
j
X
c
T
M
,
f
<
f
c
Z^{TM}=\frac{\gamma}{j\omega\varepsilon}=\begin{cases}\frac1{\omega\varepsilon}\sqrt{\omega^2\varepsilon\mu-(\frac {m\pi}{a})^2-(\frac{n\pi}{b})^2}=R^{TM},\quad\quad \quad\quad f>f_c\\ -j\frac1{\omega\varepsilon}\sqrt{(\frac{m\pi}{a})^2+(\frac{n\pi}{b})^2-\omega^2\varepsilon\mu}=-jX_c^{TM},\quad \quad f<f_c\end{cases}
ZTM=jωεγ={ωε1ω2εμ−(amπ)2−(bnπ)2=RTM,f>fc−jωε1(amπ)2+(bnπ)2−ω2εμ=−jXcTM,f<fc
Z T E = j ω μ γ = { 1 ω μ 1 ω 2 ε μ − ( m π a ) 2 − ( n π b ) 2 = R T M , f > f c j ω μ 1 ( m π a ) 2 + ( n π b ) 2 − ω 2 ε μ = j X c T M , f < f c Z^{TE}=\frac{j\omega\mu}{\gamma}=\begin{cases}\frac1{\omega\mu}\frac1{\sqrt{\omega^2\varepsilon\mu-(\frac {m\pi}{a})^2-(\frac{n\pi}{b})^2}}=R^{TM},\quad\quad \quad\quad\quad\quad\quad f>f_c\\ j\omega\mu\frac1{\sqrt{(\frac{m\pi}{a})^2+(\frac{n\pi}{b})^2-\omega^2\varepsilon\mu}}=jX_c^{TM},\quad \quad\quad\quad\quad\quad\quad f<f_c\end{cases} ZTE=γjωμ=⎩⎨⎧ωμ1ω2εμ−(amπ)2−(bnπ)21=RTM,f>fcjωμ(amπ)2+(bnπ)2−ω2εμ1=jXcTM,f<fc
主模 T E 10 TE_{10} TE10的传输特性
用主模传输的重点问题在于单模传输 单模传输 单模传输 单模传输
场分布
至于为什么
T
E
10
TE^{10}
TE10是主模的话,就不说了,你只要把 m,n的各个值代进去纵横关系式,就可以知道了
E
y
=
ω
μ
a
π
H
0
s
i
n
π
a
x
c
o
s
(
ω
t
−
β
z
−
π
2
)
E_y=\frac{\omega\mu a}{\pi}H_0sin{\frac{\pi}ax}cos(\omega t-\beta z-\frac\pi2)
Ey=πωμaH0sinaπxcos(ωt−βz−2π)
H
x
=
β
a
π
H
0
s
i
n
π
a
x
c
o
s
(
ω
t
−
β
z
+
π
2
)
H_x=\frac{\beta a}{\pi}H_0sin{\frac{\pi}ax}cos(\omega t-\beta z+\frac\pi2)
Hx=πβaH0sinaπxcos(ωt−βz+2π)
H
z
=
H
0
c
o
s
π
a
x
c
o
s
(
ω
t
−
β
z
)
H_z=H_0cos\frac\pi a xcos(\omega t-\beta z)
Hz=H0cosaπxcos(ωt−βz)
…其他三个为0…
传输特性
根据前面说的那些,代入m=1,n=0得:
f
c
=
1
2
a
ε
μ
f_c=\frac1{2a\sqrt{\varepsilon\mu}}
fc=2aεμ1
λ
c
=
2
a
\lambda_c=2a
λc=2a
β
=
k
1
−
(
f
c
f
)
2
=
ω
2
ε
μ
−
(
π
a
)
2
\beta=k\sqrt{1-({\frac {f_c}{f}})^2}=\sqrt{\omega^2\varepsilon\mu-(\frac{\pi}{a})^2}
β=k1−(ffc)2=ω2εμ−(aπ)2
λ
g
=
2
π
β
=
2
π
k
1
1
−
(
f
c
f
)
2
=
2
π
ω
2
ε
μ
−
(
π
a
)
2
\lambda_g=\frac{2\pi}{\beta}=\frac{2\pi}{k}\frac1{\sqrt{1-({\frac {f_c}{f}})^2}}=\frac{2\pi}{\sqrt{\omega^2\varepsilon\mu-(\frac{\pi}{a})^2}}
λg=β2π=k2π1−(ffc)21=ω2εμ−(aπ)22π
v
p
=
ω
β
=
v
1
−
(
f
c
f
)
2
=
ω
ω
2
ε
μ
−
(
π
a
)
2
v_p=\frac{\omega}{\beta}=\frac v{\sqrt{1-({\frac {f_c}{f}})^2}}=\frac{\omega}{\sqrt{\omega^2\varepsilon\mu-(\frac{\pi}{a})^2}}
vp=βω=1−(ffc)2v=ω2εμ−(aπ)2ω
Z
T
E
=
η
1
1
−
(
f
c
f
)
2
=
ω
μ
1
ω
2
ε
μ
−
(
π
a
)
2
Z^{TE}=\eta\frac1{\sqrt{1-({\frac {f_c}{f}})^2}}=\omega\mu\frac1{\sqrt{\omega^2\varepsilon\mu-(\frac{\pi}{a})^2}}
ZTE=η1−(ffc)21=ωμω2εμ−(aπ)21
结语
因为这里写了比较多的波动方程,所以会有点长!








 本文深入探讨了电磁波在波导中的传输特性,重点介绍了纵向场量法和矩形波导中的TM与TE波。通过解析波动方程,详细分析了TEM波的存在条件、传播特性及波阻抗等内容。
本文深入探讨了电磁波在波导中的传输特性,重点介绍了纵向场量法和矩形波导中的TM与TE波。通过解析波动方程,详细分析了TEM波的存在条件、传播特性及波阻抗等内容。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










