前言
列生成算法是求解大规模线性规划的有效手段之一,对于难以直接求解的大规模线性规划问题,列生成在某些场景能够缩小问题规模,降低问题求解难度,在可接受的时间内精确求解问题。列生成的基本思路是将一个原问题从一个小的模型开始,即一开始只考虑模型的少量列(变量),然后通过建立子问题,寻找满足进基条件的列,将这些列添加到主模型,直到找不到能够进基的列,那么这个时候我们求解主模型得到的解将等同于包含所有变量的大规模线性问题的解。试想一下,对于某些生产实际问题,其决策变量可能达到百万甚至千万级,使用求解器直接求解的难度可想而知,但是使用列生成的手段,我们最后求解的主模型可能包含的变量数仅仅在几千的数量级。以下列生成的基本流程图。
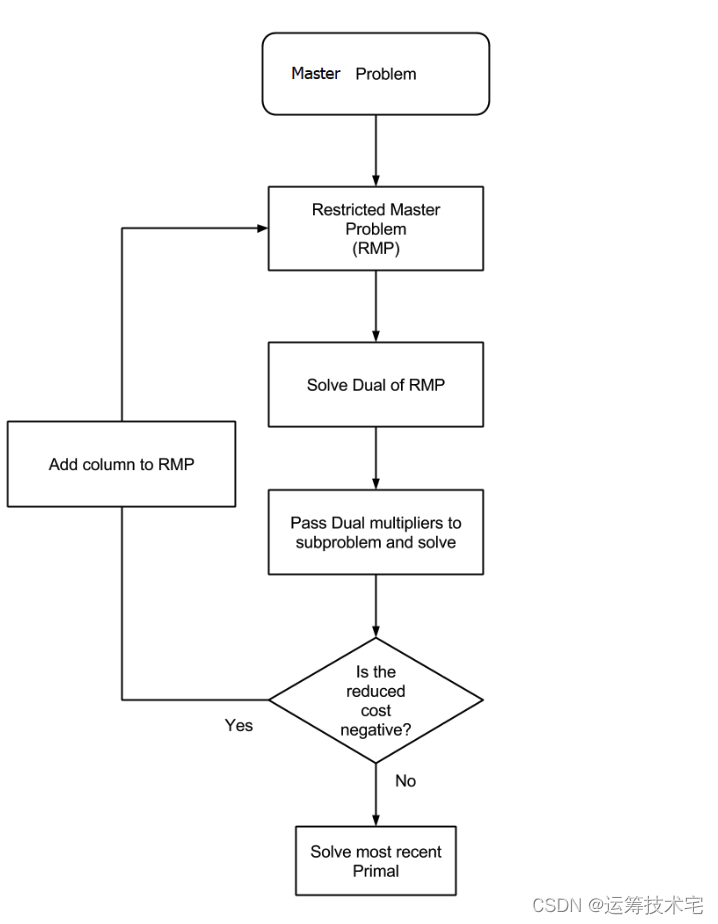
切割问题
切割问题是典型的生产实际问题,在很多卷纸厂、钢材厂都会碰到此类问题,其问题大致可描述为某工厂存在固定长度的钢材原料,现在接到订单,需要个性化定制不同长度的钢材若干,需要确定钢材的切割方案,使得在满足订单需求的情况下使用最少数量的钢材原料,以下是一个具体实例:

此问题也可以按常规思路建模,其建模思路如下:

可以看到,模型本身比较复杂,而且钢材的最大用量不好界定,对于生产实际中的大规模问题,具有相当大的求解难度,那么我们也可以换个角度,按照如下思路进行建模求解:

可以看到,按照新的思路建模,模型更加简洁,然而困难在于难以写出每种切割方案,直接求解显然是不可行,考虑使用列生成算法求解该问题,初始时候,随意给出切割方案,然后使用子问题在满足切割约束的情况下生成新的切割方案即可,以次作为列生成的初始主模型,下图给出了可行的切割方案,并建立了初始主模型。
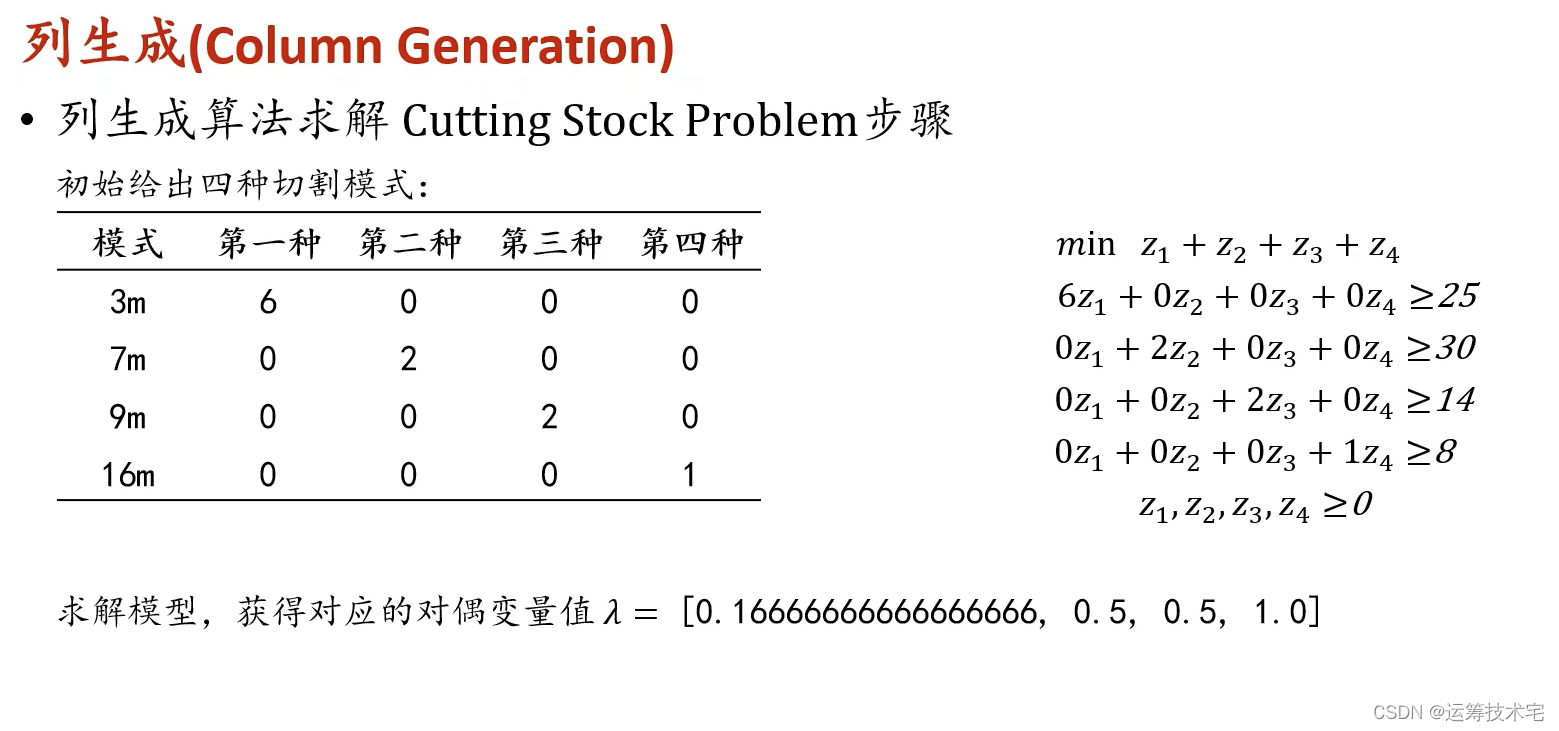
主模型建立完成后,可求解模型获得对应的对偶变量值dual=[0.166666,0.5,0.5,1],此时根据对偶值和切割长度约束建立子问题模型,目标函数是最小化列的检验数,约束为切割方案不超过钢材原料的长度,其中c_i表示此切割方案下第i种订单需求的切割数量。

一旦找到检验数小于0的列,那么将此列作为进基列添加到主模型,并重新求解主模型,获得新的对偶值,依据新的对偶值求解新的子问题,直到找不到满足进基条件的列,那么我们我们就完成了列生成的过程,求解此时的模型所得的解即最优解。
实现
from gurobi import *
import numpy as np
typesDemand=[3,7,9,16]#需求长度
quantityDemand=[25,30,14,8]#需求数量
length=20#钢管长度
#模型
mainModel=Model('Main Model')
subModel=Model('SubModel')
#变量
y=mainModel.addVars(len(typesDemand),obj=1,vtype='C',name='y')
#约束
mainModel.addConstrs(((y[i]*(length//typesDemand[i]))>=quantityDemand[i]\
for i in range(len(typesDemand))),name='mainCon')
#求解主问题
mainModel.Params.OutputFlag=0
mainModel.optimize()
#获取对偶值
Dual=mainModel.getAttr(GRB.Attr.Pi,mainModel.getConstrs())
#添加子问题变量
c=subModel.addVars(len(typesDemand),obj=Dual,vtype='I',name='c')
#添加子问题约束
subModel.addConstr(c.prod(typesDemand)<=length,name='subCon')
#求解子问题
subModel.setAttr(GRB.Attr.ModelSense,-1)#最大化
subModel.Params.OutputFlag=0
subModel.optimize()
# 根据 reduced cost 添加进基列
while subModel.objVal>1:
#获取切割方案
columnCoeff=subModel.getAttr('x',subModel.getVars())
#定义列
column=Column(columnCoeff,mainModel.getConstrs())
#添加列
mainModel.addVar(obj=1.0,vtype='C',column=column)
#求解更新后的主问题
mainModel.Params.OutputFlag=0
mainModel.optimize()
#更新对偶值
Dual=mainModel.getAttr(GRB.Attr.Pi,mainModel.getConstrs())
#重新求解子问题(修改目标函数系数)
for i in range(len(typesDemand)):
c[i].obj=Dual[i]
subModel.Params.OutputFlag=0
subModel.optimize()
#将主模型变量类型改成整型
for v in mainModel.getVars():
v.setAttr('vtype',GRB.INTEGER)
#求解主模型
mainModel.Params.OutputFlag=0
mainModel.optimize()
#输出
print('最少使用钢材数为:',mainModel.objVal)
for i in range(len(mainModel.getVars())):
v=mainModel.getVars()[i]
if v.x>0:
print('方案{}切割次数为:'.format(i),v.x)
求解结果
该问题最后的主模型如下:
\ Model Main Model
\ LP format - for model browsing. Use MPS format to capture full model detail.
Minimize
y[0] + y[1] + y[2] + y[3] + C4
Subject To
mainCon[0]: 6 y[0] + 2 C4 >= 25
mainCon[1]: 2 y[1] + 2 C4 >= 30
mainCon[2]: 2 y[2] >= 14
mainCon[3]: y[3] >= 8
Bounds
End
可以看到,模型仅仅在原来4列的基础上添加了一列(C4)即求解到了最优解,因此求解此类问题,根本就不需要枚举所有的列即可进行高效求解,最终切割方案如下:
最少使用钢材数为: 30.0
方案2切割次数为: 7.0
方案3切割次数为: 8.0
方案4切割次数为: 15.0
代码和列生成更进一步学习见视频:列生成






















 757
757











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








