利用K-Means算法对三国志武将非监督分类

思路：

        当参考三国志游戏武将的统率和武力数值，我们可以使用K-Means算法对其进行分类，设定K值为2，并采用欧式距离。统率和武力数值通常被认为是判断武将是否为武官的重要因素。由于本次实验样本较少，仅有20个，因此在精度方面可能稍显不足。

        

        

K-Means算法原理：

       K-Means算法可以被描述为对集合X进行划分，通过最小化损失函数来选取最优的划分。在这个过程中，算法不断迭代，通过优化聚类中心来减小样本点与其所属聚类中心的距离，以实现对数据集的有效划分。

        采用欧氏距离作为样本之间的距离d(xi,xj)：

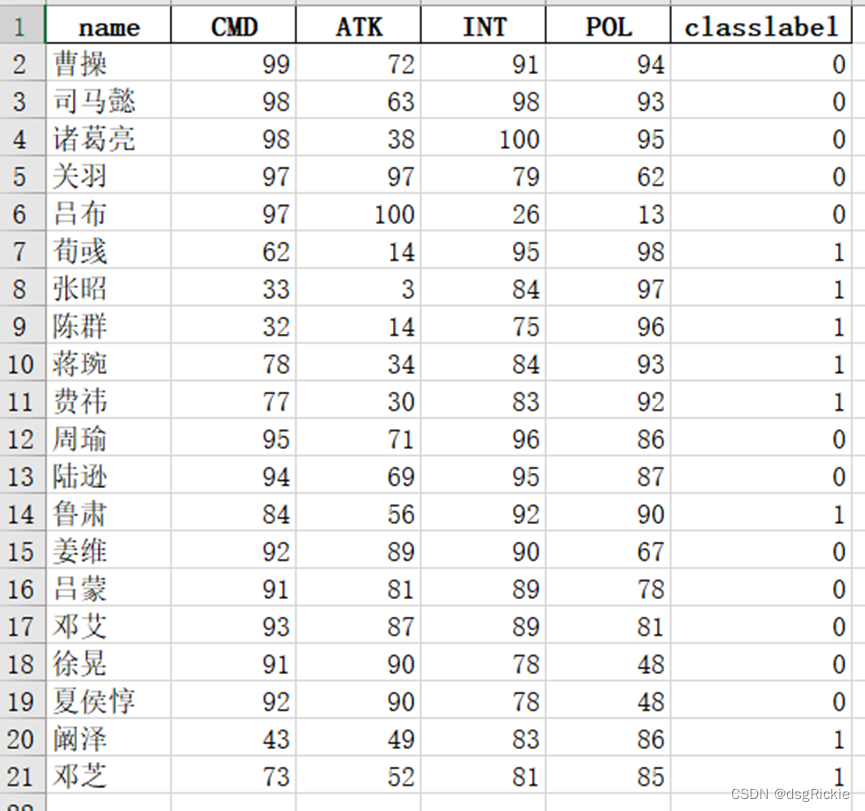
先验知识：

        先验知识展示：预先划分文武官分类

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
 
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号 #有中文出现的情况，需要u'内容
# 读取数据
filepath = 'sgz.xlsx'
data = pd.read_excel(filepath)

# 提取前两列数据
x = data.iloc[:, 1]
y = data.iloc[:, 2]

# 添加约束条件
constraint_data = data[data.iloc[:, 5] == 0]  # 第五列的值等于0
constraint_x = constraint_data.iloc[:, 1]     #统率
constraint_y = constraint_data.iloc[:,2]      #武力值

# 绘制二维图像
plt.plot(x, y, 'o', label='所有人物')  # 使用圆点标记绘制所有数据点
plt.plot(constraint_x, constraint_y, 'ro', label='武官')  # 使用红色圆点标记绘制符合约束条件的数据点
plt.xlabel('统率')
plt.ylabel('武力值')
plt.title('二维图像')
plt.legend()  # 添加图例
plt.show()

        显示效果：

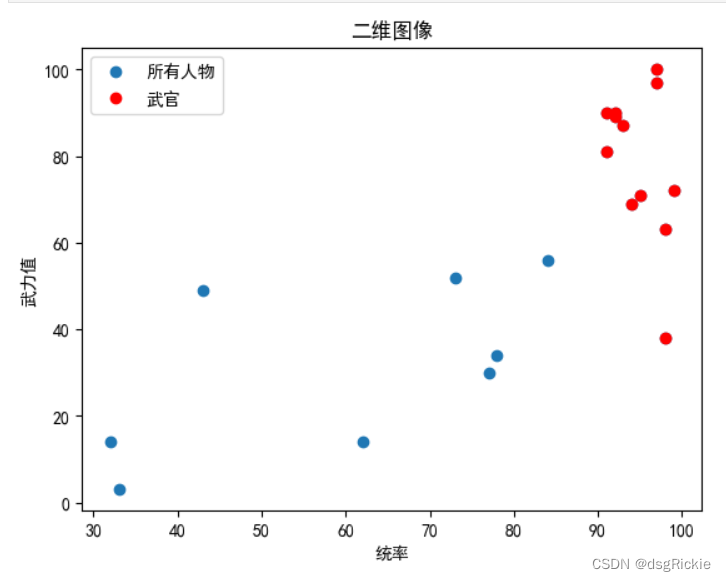
        按统率值倒序对样本数据排序：

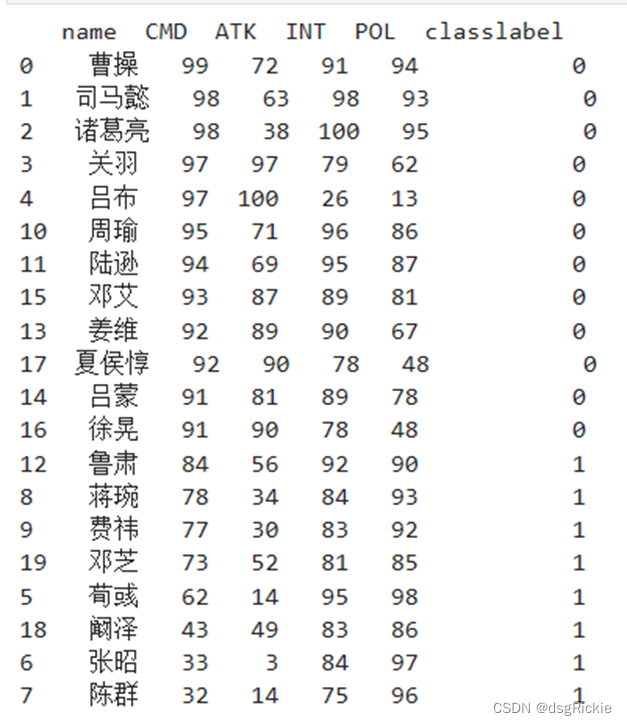
k-means非监督分类：

        接下来，我们将忽略先前的预先划分标签，使用K-Means算法对样本进行非监督分类：

使用sklearn的方式：

from sklearn.cluster import KMeans
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
 
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号 #有中文出现的情况，需要u'内容
# 读取数据
filepath = 'sgz.xlsx'
data = pd.read_excel(filepath)
# 选择第二和第三列作为训练数据
training_data = data.iloc[:, [1, 2]]
kmeans = KMeans(n_clusters=2)  # 设置聚类的数量为2
kmeans.fit(training_data)  # 使用选择的数据进行训练
y_kmeans = kmeans.predict(training_data)

# 获取聚类中心的坐标
centers = kmeans.cluster_centers_

# 绘制散点图和聚类中心
plt.scatter(training_data.iloc[:, 0], training_data.iloc[:, 1], c=y_kmeans, s=50, cmap='viridis', alpha=0.5)
plt.scatter(centers[:, 0], centers[:, 1], c='red', s=200, alpha=0.7)  # 绘制聚类中心
plt.xlabel('统率')
plt.ylabel('武力值')
plt.show()

        效果：K-means根据分布规律划分成2个分类，其中红色圆点为聚类中心。

自定义函数方式：

聚类方法思路：

函数 KMeans(X, k, max_iters):

    随机初始化聚类中心 centroids 为 X 中的 k 个样本点

    循环 max_iters 次:

        计算每个样本点到各个聚类中心的距离 distances

        将样本点分配到最近的聚类中心，得到类别标签 labels

        更新聚类中心为每个类别中样本点的均值，得到新的聚类中心 new_centroids

        如果新的聚类中心和原来的聚类中心相等，停止迭代

        否则，更新聚类中心为新的聚类中心

返回类别标签 labels 和聚类中心 centroids

代码：

def kmeans(X, k, max_iters=100):
    # 随机初始化聚类中心,k=2时选取两行数据
    centroids = X[np.random.choice(range(X.shape[0]), k, replace=False)]
    for _ in range(max_iters):

        # 计算每个样本点与每个聚类中心的距离

        # X 是一个二维数组，而 centroids 是一个一维数组，需要为 centroids 添加一个新的轴，进行运算
        distances = X - centroids[:, np.newaxis]#distances将是一个20行2列的矩阵，其中每一行表示每个样本点到两个聚类中心的距离。
        distances_squared = distances**2  # 求差值的平方
        distances_sum = distances_squared.sum(axis=2)  # 对平方差值沿着第三个维度（聚类中心）求和
        distances = np.sqrt(distances_sum)  # 对和进行开方，得到实际的距离

        
        # 分配每个样本点到最近的聚类中心
        labels = np.argmin(distances, axis=0)
        
        # 更新聚类中心
        new_centroids = []
        for i in range(k):
            # 选择所有属于第 i 个簇的样本点
            cluster_points = X[labels == i]
            # 计算选中的样本点沿着第一个维度（行）的平均值，即计算出新的第 i 个簇的聚类中心
            centroid = cluster_points.mean(axis=0)
            new_centroids.append(centroid)
        
        # 将新的聚类中心转换为数组
        new_centroids = np.array(new_centroids)

        # 如果聚类中心不再改变，提前结束
        if np.all(centroids == new_centroids):
            break
        centroids = new_centroids
    return labels,centroids
# 使用自行实现的KMeans算法进行聚类
y_kmeans,centroids = kmeans(training_data.values, 2)
print(centroids)
# 绘制散点图
plt.scatter(training_data.iloc[:, 0], training_data.iloc[:, 1],c=y_kmeans, s=50, cmap='viridis', alpha=0.5)
plt.scatter(centroids[:, 0], centroids[:, 1], c='r', s=200, alpha=0.5)
plt.xlabel('统率值')
plt.ylabel('武力值')
plt.show()

        效果：

        聚类中心坐标：

[[93.58333333 80.41666667]
 [62.         29.25      ]]

        对比数据：

        根据先验知识和非监督学习的结果进行比较可以发现，统率和武力值与武官分类之间存在着密切的联系。这种联系的存在验证了先验知识的有效性，同时也突显了统率和武力值在判断武官身份上的重要作用。