【NeurIPS 2019】最大熵的蒙特卡洛规划算法

• 论文题目：Maximum Entropy Monte-Carlo Planning

所解决的问题？

1. 作者提出了一个新的stochastic softmax bandit框架；
2. 将其扩展到MCTS上，得到了 Maximum Entropy for Tree Search (MENTS)算法。

  将softmax state value 引入，在back-propaganda过程中会更容易收敛。作者在理论和实验部分都验证了这两个想法。

背景

MCTS

   Monte Carlo Tree Search (MCTS) 是一种非常好的能够获取全局最优的算法，同时也可以通过引入先验知识对其进行加强。它的核心问题在于exploitation和exploration的平衡。而MCTS的收敛性高度依赖于state value 的 estimation。而MCTS通过simulation获得当前状态的估计这种做法并不是非常高效，因此在sample的过程中你的policy会发生改变，导致你的序列期望收益会发生漂移(drift)，因此 UCT can only guarantee a polynomial convergence rate of finding the best action at the root。MCTS主要可以分为两步：1. tree policy选择action，直到到达叶子节点。2. 一个evaluation function需要评估simulation return，你可以选择近函数近似的方式来逼近这个值，但是在MCTS中采用的是roll-out policy获取simulation return。

  maximum upper confidence bound(UCB)算法用于平衡探索和利用：

$$\mathrm{UCB}(s,a)=Q(s,a)+c\sqrt{\frac{\log N(s)}{N(s,a)}}$$

  其中$N(s)={\sum }_{a}N(s,a)$，$c$是控制exploration的参数。

Maximum Entropy Policy Optimization

  最大熵的策略优化问题其实就是在expected reward目标上引入一个entropy的约束。可表示为：

max ⁡ π { π ⋅ r + τ H ( π ) } \max _{\pi}\{\pi \cdot \mathbf{r}+\tau \mathcal{H}(\pi)\} πmax​{π⋅r+τH(π)}

  其中$\tau$是控制exploration的参数。定义softmax ${\mathcal{F}}_{\tau }$和soft indmax ${\mathbf{f}}_{\tau }$：

f τ ( r ) = exp ⁡ { ( r − F τ ( r ) ) / τ } \mathbf{f}_{\tau}(\mathbf{r})=\exp \left\{\left(\mathbf{r}-\mathcal{F}_{\tau}(\mathbf{r})\right) / \tau\right\} fτ​(r)=exp{(r−Fτ​(r))/τ}

$${\mathcal{F}}_{\tau }(\mathbf{r})=\tau \log \sum _a\exp (r(a)/\tau )$$

  其中的关系为：

F τ ( r ) = max ⁡ π { π ⋅ r + τ H ( π ) } = f τ ( r ) ⋅ r + τ H ( f τ ( r ) ) \mathcal{F}_{\tau}(\mathbf{r})=\max _{\pi}\{\pi \cdot \mathbf{r}+\tau \mathcal{H}(\pi)\}=\mathbf{f}_{\tau}(\mathbf{r}) \cdot \mathbf{r}+\tau \mathcal{H}\left(\mathbf{f}_{\tau}(\mathbf{r})\right) Fτ​(r)=πmax​{π⋅r+τH(π)}=fτ​(r)⋅r+τH(fτ​(r))

  因此用softmax value function去替代hard-max operator可以得到softmax operator：

$$Q_{\mathrm{sft}}^{\ast }(s,a)=R(s,a)+{\mathbb{E}}_{s^{\prime }|s,a}\left[V_{\mathrm{sft}}^{\ast }\left(s^{\prime }\right)\right]$$

V s f t ∗ ( s ) = τ log ⁡ ∑ a exp ⁡ { Q s f t ∗ ( s , a ) / τ } V_{\mathrm{sft}}^{*}(s)=\tau \log \sum_{a} \exp \left\{Q_{\mathrm{sft}}^{*}(s, a) / \tau\right\} Vsft∗​(s)=τloga∑​exp{Qsft∗​(s,a)/τ}

  最后可以得到optimal softmax policy：

π s f t ∗ ( a ∣ s ) = exp ⁡ { ( Q s f t ∗ ( s , a ) − V s f t ∗ ( s ) ) / τ } \pi_{\mathrm{sft}}^{*}(a | s)=\exp \left\{\left(Q_{\mathrm{sft}}^{*}(s, a)-V_{\mathrm{sft}}^{*}(s)\right) / \tau\right\} πsft∗​(a∣s)=exp{(Qsft∗​(s,a)−Vsft∗​(s))/τ}

Softmax Value Estimationin Stochastic Bandit

  在stochastic bandit中，环境给定的reward是随机的，或者说会满足一个分布。stochastic softmax bandit 问题与传统的stochastic bandits问题的区别在于，它不是期望去找到最大化期望奖励的policy，而是去估计softmax value $V_{sft}^{\ast }={\mathcal{F}}_{\tau }(\mathbf{r})$。定义 U t = ∑ a exp ⁡ { r ^ t ( a ) / τ } U_{t}=\sum_{a} \exp \left\{\hat{r}_{t}(a) / \tau\right\} Ut​=∑a​exp{r^t​(a)/τ}， U ∗ = ∑ a exp ⁡ { r t ( a ) / τ } U^{*}=\sum_{a} \exp \left\{r_{t}(a) / \tau\right\} U∗=∑a​exp{rt​(a)/τ}。因此会有$V_t={\mathcal{F}}_{\tau }({\hat{r}}_t)=\tau log{U}_t$，我们的目标就变成了最小化均方差误差$\mathcal{E}$。

$${\mathcal{E}}_t=\mathbb{E}\left[{\left({\hat{U}}^{\ast }-U_t\right)}^2\right]$$

  基于上述讨论作者提出了一种解决序贯决策中softmax value估计的办法(Empirical Exponential Weight (E2W) )，直观的理解就是期望足够的探索用于保证得到较好的估计值，进而使得policy收敛于最优策略${\pi }^{\ast }$。动作的采样分布如下所示：

$${\pi }_t(a)=\left(1-{\lambda }_t\right){\mathbf{f}}_{\tau }(\hat{\mathbf{r}})(a)+{\lambda }_t\frac{1}{|\mathcal{A}|}$$

  其中 ${\lambda }_t=\epsilon |\mathcal{A}|/\log (t+1)$，表示探索的衰减系数。

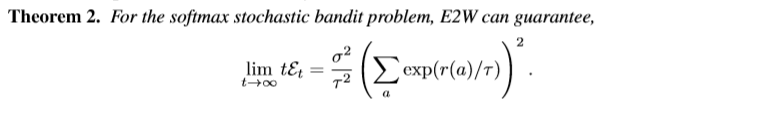
所采用的方法？

  作者将MCTS和maximum entropy policy结合起来，得到MENTS算法，能够获得更快的收敛速度。两点创新：

1. 使用E2W算法作为树搜索的策略；

$${\pi }_t(a|s)=\left(1-{\lambda }_s\right){\mathbf{f}}_{\tau }\left({\mathbf{Q}}_{\mathrm{sft}}(s)\right)(a)+{\lambda }_s\frac{1}{|\mathcal{A}|}$$

2. 使用softmax value评估每个节点并用于simulations的反向传播。

  其中Q-Value的估计使用softmax backup。

$$Q_{\mathrm{sft}}\left(s_t,a_t\right)=\{\begin{array}{ll}r\left(s_t,a_t\right)+R& t=T-1\\ r\left(s_t,a_t\right)+{\mathcal{F}}_{\tau }\left({\mathrm{Q}}_{\mathrm{sft}}\left(s_{t+1}\right)\right)& t<T-1\end{array}$$

取得的效果？

我的微信公众号名称：小小何先生
公众号介绍：主要研究深度学习、强化学习、机器博弈等相关内容！期待您的关注，欢迎一起学习交流进步！