北京大学 人工智能实践：Tensorflow笔记——曹健（writed by Enigmalgia）

可以看下我转载的一篇文章机器学习入门概括

关于TensorFlow的安装 Ubuntu18.04下安装anaconda和pycharm搭建TensorFlow

贴一下TensorFlow的官方中文版教程

TensorFlow的中文API文档

曹健老师的GitHub源码

---

持续更新，在和同学交流之后被推荐了北京大学曹健老师的这门实践课，学习TensorFlow的实践。先致谢一下曹健老师！课程资源在B站和网易中国MOOC都可以找到。大三课务紧张，只能抽时间补笔记，可能更新缓慢。

目录

第一讲：概述

第二讲：Python基础

第三讲：TensorFlow框架

3.1基本概念 张量（Tensor）、计算图（Graph）、会话（Session）

3.2前向传播（搭建神经网络模型，让神经网络NN实现推理过程）

3.3反向传播（大量特征数据喂给NN，迭代优化NN参数）

第四讲、神经网络优化

4.1损失函数

---

第一讲：概述

图灵在1950年写过一篇论文《计算机器与智能》，图灵让我们思考：“机器能否拥有智能？（Can machines think？）”这个问题。图灵成功定义了什么是计算机器（即图灵机），但却不能定义什么是智能（Think）,没有办法用机器或算法来准确定义。因此图灵设计了一个模拟测试——图灵测试（一种用于判定机器是否具有智能的试验方法）。图灵测试的核心想法是要求计算机在没有直接物理接触的情况下接受人类的询问，并尽可能把自己伪装成人类。

图灵测试

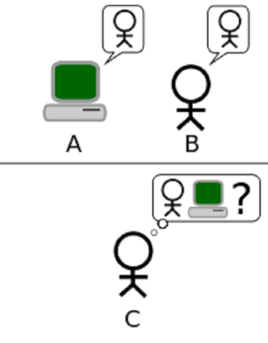
试验过程：提问者和回答者隔开，提问者通过一些装置（如键盘）向机器随意提问。多次测试，如果有超过30%的提问者认为回答问题的是人而不是机器，那么这台机器就通过测试，具有了人工智能。

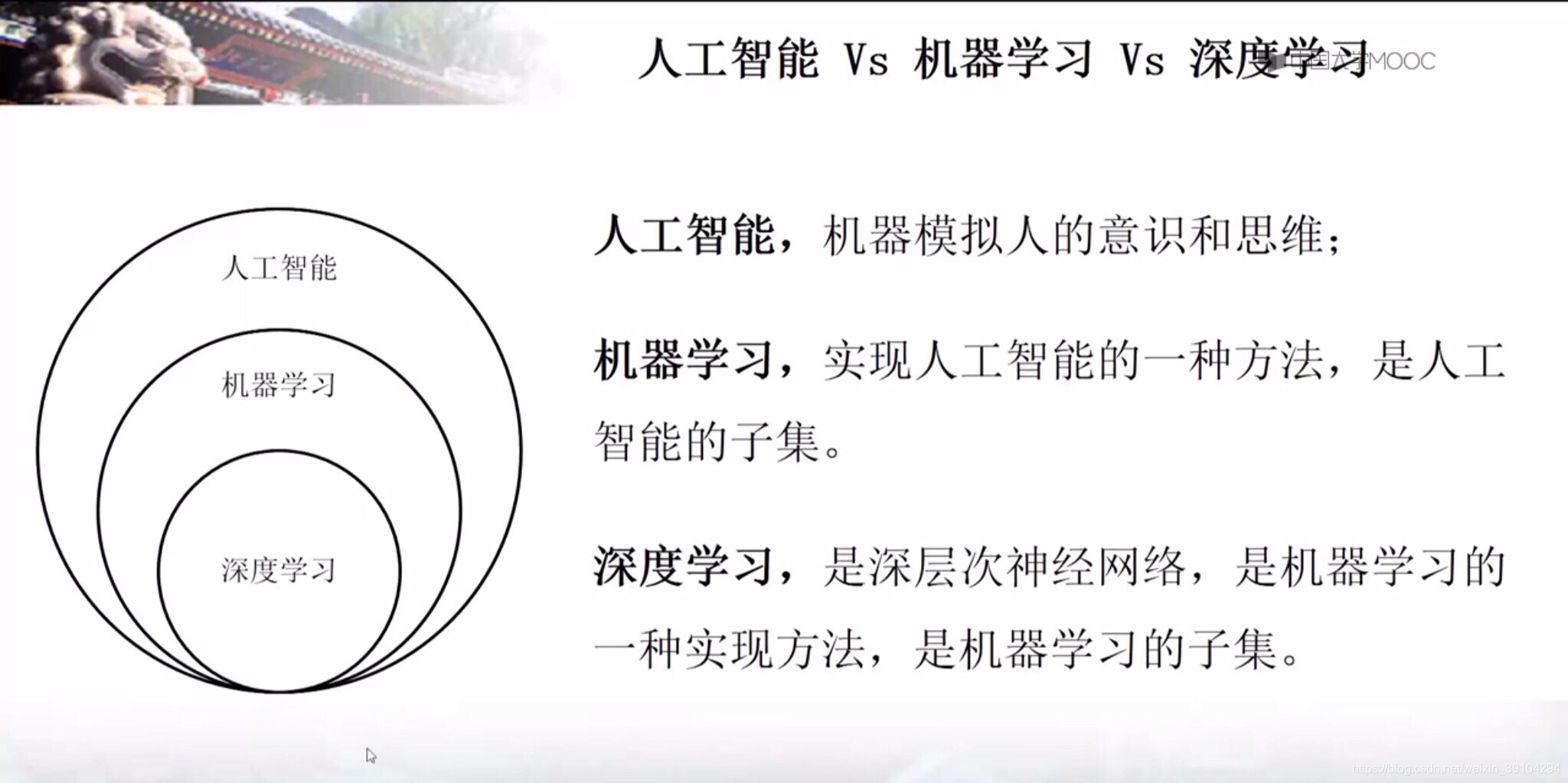
人工智能：机器模拟人的意识和思维。

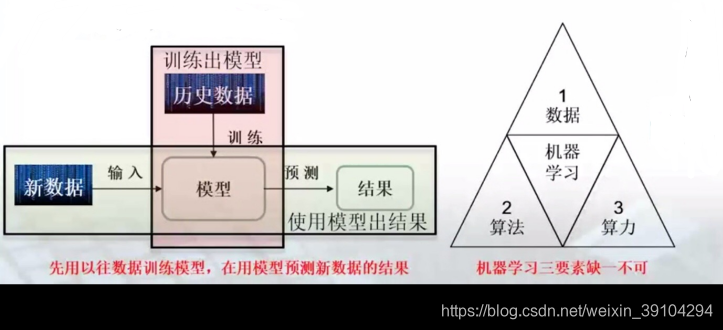
机器学习：机器学习是一种统计学方法，计算机利用已有的数据，得出某种模型，再利用这个模型来预测结果。在历史数据的基础上，不断训练，随经验增加，预测的效果会更好。（以预测班车到达时间为例）

add.这里我补充一下“花书”中对于机器学习的描述：Ai系统需要具备自己获取知识的能力，即从原始数据中提取模式的能力，这种能力被称为机器学习。

机器学习

深度学习（深度神经网络）：模仿人类的神经网络，在计算机中建立计算机的神经网络。

add.“花书”中对于深度学习的描述：让计算机从经验中学习，并根据层次化的概念体系来理解世界，而每个概念则通过与某些相对简单的概念自己啦的关系来定义。让计算机从经验中获取知识，可以避免由人类来给计算机形式化地指定它所需要的所有知识。层次化的概念让计算机构建相对较简单的概念来学习复杂的概念。如果绘制出这些概念如何建立在彼此之上的图，我们将得到一张“深（deep）层次很多的”图。基于这些原因，我们称这种方法为深度学习。

（在下面的计算机网络的发展中，可以更加直观的理解到深层网络。1986年是一层网络，2012年到了CNN出现了4层。层次化越来越深，对于知识的理解程度也越来越深刻。）

计算机中的神经元模型

深度神经网络的发展过程： 

标题计算机网络的发展

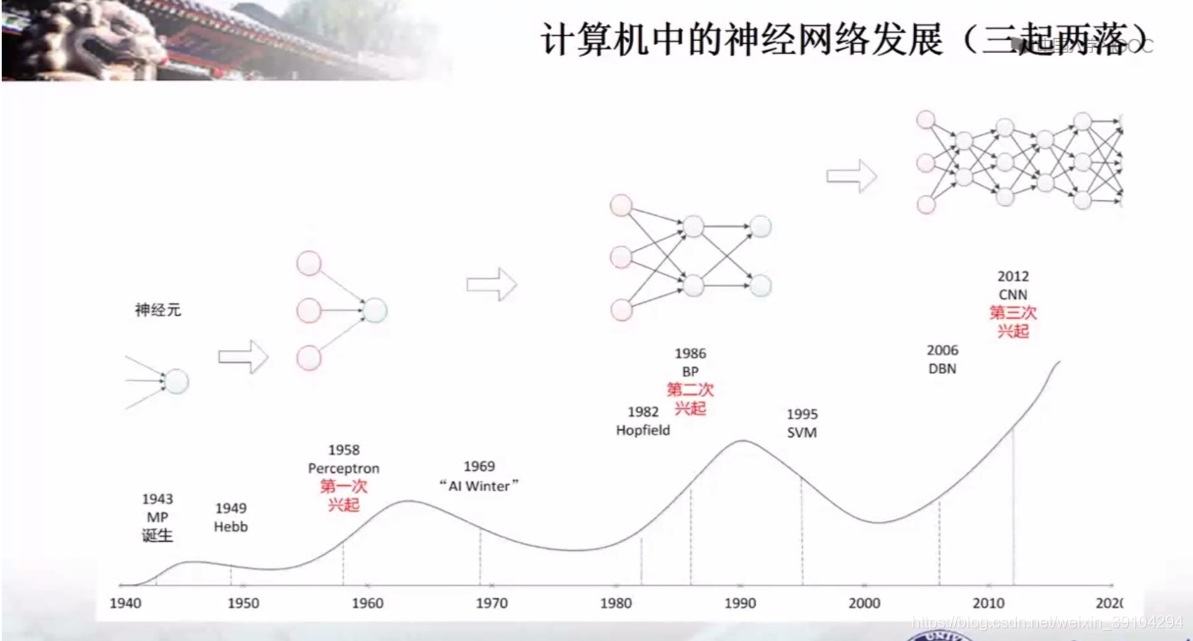
机器学习最主要的应用：

• 对于连续数据的预测（预测房价）
• 对于离散数据的分类（判定是否为肿瘤）

人工智能&机器学习&深度学习

---

第二讲：Python基础

就不记录了 直接翻看廖雪峰老师的博客入门或者其他材料即可

---

第三讲：TensorFlow框架

主要内容：张量、计算图和会话，以及讲解神经网络的前向传播和后向传播的实现方法；最终学会搭建神经网络，并总结神经网络的一般格式

3.1基本概念 张量（Tensor）、计算图（Graph）、会话（Session）

基于TensorFlow的NN：用张量（tensor）表示数据，用计算图（Graph）搭建神经网络，用会话（Session）执行计算图，优化线上的权重（参数w），得到模型

张量（tensor）：多维数组（列表）

阶：张量的维数

张量可以表示0阶到n阶数组（列表）

维数	阶	名字	例子
0-D	0	标量 scalar	s=1，2，3
1-D	1	向量 vector	v=[1,2,3]
2-D	2	矩阵 matrix	m=[[1,2,3],[4,5,6],[7,8,9]
n-D	n	张量 tensor	t=[[[....(张量的维度可以通过方括号的个数来确定）

数据类型 ：tf.float32       tf.int32  ···

# 导入TensorFlow模块
import tensorflow as tf

# 数据类型
# 定义一个张量[1.0,2.0]
a=tf.constant([1.0,2.0])
# 定义一个张量[3.0,4.0]
b=tf.constant([3.0,4.0])
# 实现一维向量加法
result = a+b
# 输出 
print(result)
# 结果如下（输出的结果不是运算的结果） add:0 节点名:第0个输出；shape=(2,) shape维度  (2,)一维数组长度为2 dtype数据类型
# Tensor("add:0", shape=(2,), dtype=float32)
# result是一个名称为add:0的张量，shape=(2,)表示一维数组长度为2,dtype=float32表示数据类型为浮点型

计算图（Graph）：搭建神经网络的计算过程，只搭建不运算 

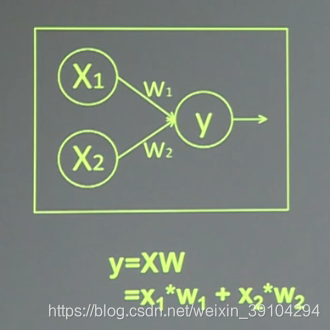
在前一讲中我们讲到，神经网络是由很多个神经元组成的。每个神经元的基本操作为数学运算中的加、乘运算。其中每条线上的w分别是输入在结果中占的权重。x1、x2表示输入，w1、w2分别是x1到y和x2到y的权重，y=x1*w1+x2*w2。

计算图（graph）

import tensorflow as tf
# 计算图（Graph）搭建神经网络的计算过程，只搭建不运算
#  y = x1*W1 + x2*W2 其中w1和w2 分别是x1和x2到y的权重值
x1=tf.constant([[1.0,2.0]])  # x1是一个1行2列的张量
x2=tf.constant([[3.0],[4.0]]) #x2是一个2行1列的张量
y=tf.matmul(x1,x2) #用tf调用matmul# 实现矩阵乘法
print(y)
# 结果如下（输出的结果不是运算的结果，是一个张量Tensor）
# Tensor("MatMul:0", shape=(1, 1), dtype=float32)

会话（Session）：执行计算图中的节点运算，通过下面的代码将结果存入会话（Session）中，再通过输出sess对象得到结果

with tf.Session() as sess:
    print(sess.run(result))

则上面两个实例关于向量&关于矩阵的运算都可以输出结果，如下

#向量加法运算
import tensorflow as tf
a=tf.const