16# 电磁感应

1变化的电磁场能产生电流

奥斯特在1819年发现稳定的电流产生稳定的磁场，不久法拉第觉得也许稳定的磁场也能产生稳定的电流，他就做了如下图的实验。实验中电流通过螺线管产生稳定的磁场，在螺线管外有电路二，在前期实验中电路二一直没有电流产生，直到他有一天开关电路中发现了线路二有电流，于是法拉第得出了结论，变化的电磁场能产生电流。

2楞次定律

如上图将一根磁铁靠近线圈，线圈会产生电流从而电磁场，产生电磁场方向与电磁场改变的方向相反，电流想反抗电磁场的变化，这就叫楞次定律

3法拉第电磁感应定律

磁通量的定义

楞次定律是永远反抗磁通变化的，下图公式中，感生电动势公式中下图有负号。

法拉第电磁感应定律

顺时针dA将进入黑板，垂直于黑板
逆时针dA朝向你
面不一定要是平的，可以使平的也可以是如帽子一样的曲面，可以想象磁通是水流穿过袋子，出去的面可以是平面也可以是袋子外表面的曲面。
基尔霍夫曾说过EdL的闭合路径积分总是0,但是这只在保守场中成立，当有变化的磁通时这并不成立，当你有一个变化的磁通，此时导线内部的电场会变成非保守的，基尔霍夫定律只有在保守场中才成立
当你在保守场中EdL跟路径无关，从1点到2点，积分与路径无关，是两点间的电势差，然而又磁通变化后，绕圈数3圈是1圈的电势差的三倍，因为此时处理的是非保守场。

4案例

如图一个电源1v两个电阻分别为100欧姆和900欧姆，可以得到D,A之间为0.9v，如下图将电源换位向外的螺线管。假设螺线管产生的感生电流也是1v。可得：左侧电压表DA为-0.1v右侧为0.9v

基尔霍夫定律只是法拉第定律的特例

基尔霍夫定律说必须为0，法拉第定律进行修正，这个1v为EdL所做的环路闭合积分，所以当你用EdL来定义电动势，在非保守场，这与路径有关

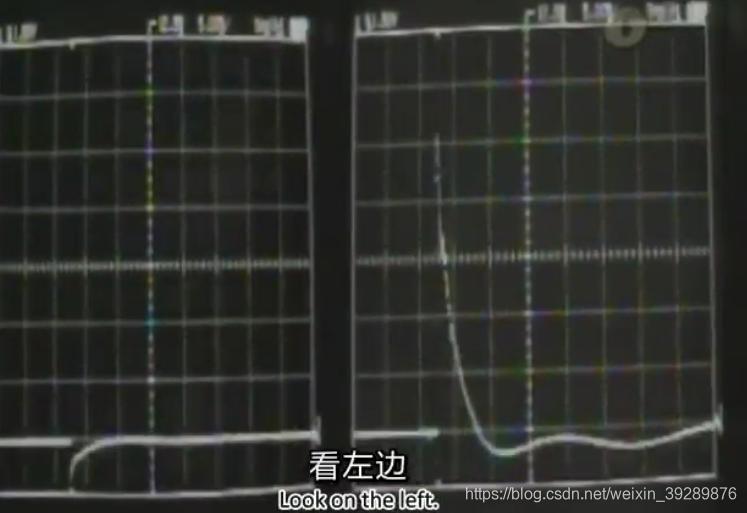
上图实验证明可看出，右边的电压变化是左边的十倍。