三角形周长最短问题_【九年级】因动点产生的线段和差问题

初中阶段,线段和、差的最值问题是一个难点.求解这类问题,关键的在于找出两个"量":一是定点,二是动点或不定点所在的定直线;进而利用"两点之间线段最短"或三角形的三边关系来解决

例 1

别让十年

后的你后

悔现在

【

思路点拨】

     

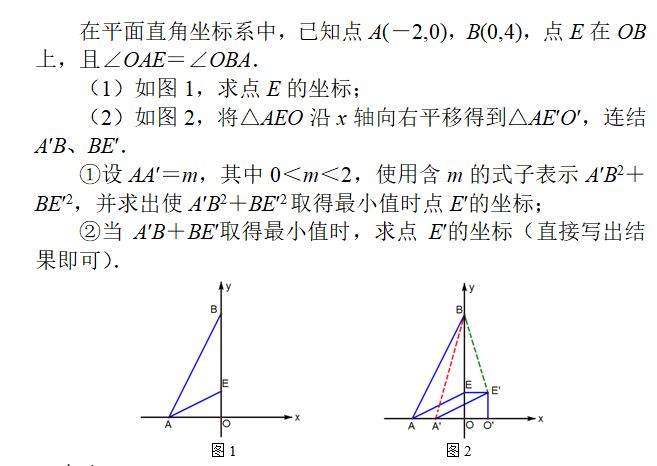
1．图形在平移的过程中，对应点的连线平行且相等，EE′＝AA′＝m

2．求A′B2＋BE′2的最小值，第一感觉是用勾股定理列关于m的式子

3．求A′B＋BE′的最小值，第一感觉是典型的“牛喝水”问题——轴对称，两点之间线段最短．

【

考点伸展】

例2

大世界
用行动

去测量

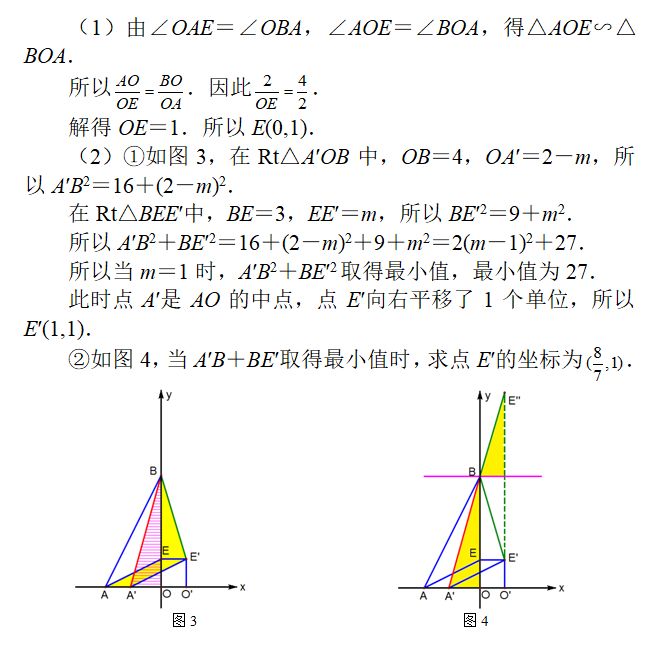
(1)求直线AC的解析式及B、D两点的坐标；

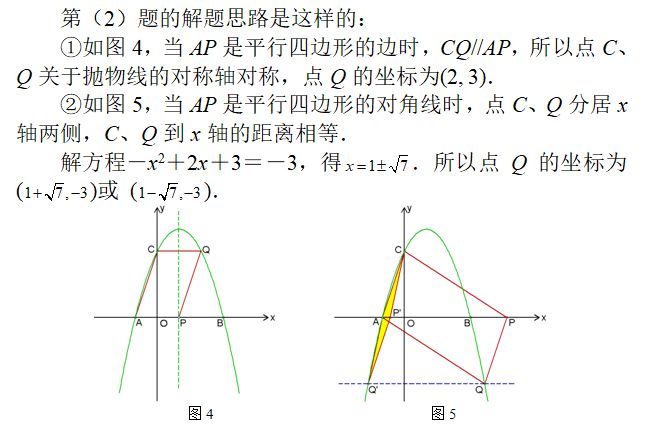
(2)点P是x轴上的一个动点，过P作直线l//AC交抛物线于点Q．试探究：随着点P的运动，在抛物线上是否存在点Q，使以A、P、Q、C为顶点的四边形是平行四边形？若存在，请直接写出符合条件的点Q的坐标；若不存在，请说明理由；

(3)请在直线AC上找一点M，使△BDM的周长最小，求出点M的坐标

【

思路点拨】

 

【

考点伸展】

练习

奋斗

世界不会

亏待你

【两点之间，线段最短

】

两条动线段的和的最小值问题，常见的是典型的“牛喝水”问题，关键是指出一条对称轴“河流”(如图1)

三条动线段的和的最小值问题，常见的是典型的“台球两次碰壁”或“光的两次反射”问题，关键是指出两条对称轴“反射镜面”(如图2)

两条线段差的最大值问题，一般根据三角形的两边之差小于第三边，当三点共线时，两条线段差的最大值就是第三边的长．如图3，PA与PB的差的最大值就是AB，此时点P在AB的延长线上，即P′．

【

垂线段最短】

如图4，正方形ABCD的边长为4，AE平分∠BAC交BC于E．点P在AE上，点Q在AB上，那么△BPQ周长的最小值是多少呢？

如果把这个问题看作“牛喝水”问题，AE是河流，但是点Q不确定啊．

第一步，应用“两点之间，线段最短”．如图5，设点B关于“河流AE”的对称点为F，那么此刻PF＋PQ的最小值是线段FQ．

第二步，应用“垂线段最短”．如图6，在点Q运动过程中，FQ的最小值是垂线段FH．

这样，因为点B和河流是确定的，所以点F是确定的，于是垂线段FH也是确定的．

点赞、转发、留言